Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T04:35:53.924Z Has data issue: false hasContentIssue false
  • English
  • Français

Open-loop control of cavity oscillations with harmonic forcings

Published online by Cambridge University Press:  12 September 2012

Denis Sipp
Denis Sipp*
Affiliation:
ONERA DAFE-The French Aerospace Lab, 8 rue des Vertugardins, 92190 Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This article deals with open-loop control of open-cavity flows with harmonic forcings. Two-dimensional laminar open-cavity flows usually undergo a supercritical Hopf bifurcation at some critical Reynolds number: a global mode becomes unstable and its amplitude converges towards a limit cycle. Such behaviour may be accurately captured by a Stuart–Landau equation, which governs the amplitude of the global mode. In the present article, we study the effect on such a flow of a forcing characterized by its frequency 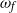, its amplitude 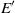and its spatial structure 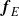. The system reacts like a forced Van der Pol oscillator. In the general case, such a forcing modifies the linear dynamics of the global mode. It is then possible to predict preferred forcing frequencies 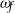, at which the global mode may be stabilized with the smallest possible forcing amplitude 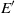. In the case of a forcing frequency close to the frequency of the global mode, a locking phenomenon may be observed if the forcing amplitude 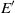is sufficiently high: the frequency of the flow on the limit cycle may be modified with a very small forcing amplitude 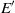. In each case, we compute all harmonics of the flow field and all coefficients that enter the amplitude equations. In particular, it is possible to find preferred forcing structures 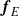that achieve strongest impact on the flow field. In the general case, these are the optimal forcings, which are defined as the forcings that trigger the strongest energy response. In the case of a forcing frequency close to the frequency of the global mode, a forcing structure equal to the adjoint global mode ensures the lowest forcing amplitude 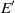. All predictions given by the amplitude equations are checked against direct numerical simulations conducted at a supercritical Reynolds number. We show that a global mode may effectively be stabilized by a high-frequency harmonic forcing, which achieves suppression of the perturbation frequencies that are lower than the forcing frequency, and that a near-resonant forcing achieves locking of the flow onto the forcing frequency, as predicted by the amplitude equations.

JFM classification

Flow Control: Instability control Nonlinear Dynamical Systems: Low-dimensional models Wakes/Jets: Separated flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 708 , 10 October 2012 , pp. 439 - 468
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alizard, F. & Robinet, J.-C. 2007 Spatially convective global modes in a boundary layer. Phys. Fluids 19 (11), 114105.Google Scholar
2. Amestoy, P. R., Duff, I. S., Koster, J. & L’Excellent, J.-Y. 2001 A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Math. Anal. Appl. 23 (1), 15–41.CrossRefGoogle Scholar
3. Amitay, M., Smith, D. R., Kibens, V., Parekh, D. E. & Glezer, A. 1998 Aerodynamic flow control over an unconventional airfoil using synthetic jet actuators. AIAA J. 39, 361–370.CrossRefGoogle Scholar
4. Barbagallo, A., Sipp, D. & Schmid, P. J. 2009 Closed-loop control of an open cavity flow using reduced-order models. J. Fluid. Mech. 641, 1–50.Google Scholar
5. Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.CrossRefGoogle Scholar
6. Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers: Asymptotic Methods and Perturbation Theory. McGraw-Hill.Google Scholar
7. Brandt, L., Sipp, D., Pralits, J. & Marquet, O. 2011 Effect of base-flow variation in noise amplifiers: the flat-plate boundary layer. J. Fluid Mech. 687, 503–528.Google Scholar
8. Choi, H., Jeon, W.-P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
9. Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.CrossRefGoogle Scholar
10. Fauve, S. 1998 Pattern forming instabilities. In Hydrodynamics and Nonlinear Instabilities (ed. Godrèche, C. & Manneville, P. ), pp. 387–492. Cambridge University Press.CrossRefGoogle Scholar
11. Giannetti, F., Camarri, S. & Luchini, P. 2010 Structural sensitivity of the secondary instability in the wake of a circular cylinder. J. Fluid Mech. 651, 319–337.Google Scholar
12. Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
13. Glezer, A. & Amitay, M. 2002 Synthetic jets. Annu. Rev. Fluid Mech. 24, 503–529.Google Scholar
14. Glowinski, R. 2003 Finite element methods for incompressible viscous flow. In Handbook of Numerical Analysis (ed. Ciarlet, P. G. & Lions, J. L. ), vol. IX. pp. 3–1176. North-Holland.Google Scholar
15. Hill, D. C. 1992 A theoretical approach for analysing the restabilization of wakes. AIAA paper 1992-0067.CrossRefGoogle Scholar
16. Huerre, P & Rossi, M. 1998 Hydrodynamic instabilities in open flows. In Hydrodynamics and Nonlinear Instabilities (ed. Godrèche, C. & Manneville, P. ), pp. 81–294. Cambridge University Press.CrossRefGoogle Scholar
17. Hwang, Y. & Choi, H. 2006 Control of absolute instability by basic-flow modification in a parallel wake at low Reynolds number. J. Fluid Mech. 560, 465–475.Google Scholar
18. Illy, H., Geffroy, P. & Jacquin, L. 2008, Observations on the passive control of flow oscillations over a cavity in a transonic regime by means of a spanwise cylinder. AIAA paper 2008-3774.CrossRefGoogle Scholar
19. Jackson, C. P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.CrossRefGoogle Scholar
20. Keirsbulck, L., El Hassan, M., Lippert, M. & Labraga, L. 2008 Control of cavity tones using a spanwise cylinder. Can. J. Phys. 86 (12), 1355–1365.Google Scholar
21. Kim, J. & Choi, H. 2005 Distributed forcing of flow over a circular cylinder. Phys. Fluids 17, 033103.CrossRefGoogle Scholar
22. Lehoucq, R. B. & Sorensen, D. C. 1996 Deflation techniques for an implicitly restarted Arnoldi iteration. SIAM J. Math. Anal. Appl. 17 (4), 789–821.CrossRefGoogle Scholar
23. Marquet, O., Sipp, D., Chomaz, J.-M. & Jacquin, L. 2008a Amplifier and resonator dynamics of a low-Reynolds-number recirculation bubble in a global framework. J. Fluid Mech. 605, 429–443.Google Scholar
24. Marquet, O., Sipp, D., Jacquin, L. & Chomaz, J.-M. 2008bMultiple time scale analysis and sensitivity analysis for the passive control of the cylinder flow. In 5th AIAA Theoretical Fluid Mechanics Conference, 23–26 June 2008, Seattle, Washington. AIAA paper 2008-4228.Google Scholar
25. Meliga, P. & Chomaz, J.-M. 2011 An asymptotic expansion for the vortex-induced vibrations of a circular cylinder. J. Fluid Mech. 671, 137–167.CrossRefGoogle Scholar
26. Meliga, P., Chomaz, J.-M. & Sipp, D. 2009 Global mode interaction and pattern selection in the wake of a disk: a weakly nonlinear expansion. J. Fluid Mech. 633, 159–189.Google Scholar
27. Meliga, P., Sipp, D. & Chomaz, J. -M. 2010 Open-loop control of compressible afterbody flows using adjoint methods. Phys. Fluids 22, 054109.Google Scholar
28. Monokrousos, A., Akervik, E., Brandt, L. & Henningson, D. S. 2010 Global three-dimensional optimal disturbances in the Blasius boundary-layer flow using time-steppers. J. Fluid Mech. 650, 181–214.Google Scholar
29. Pier, B 2003 Open-loop control of absolutely unstable domains. Proc. R. Soc. Lond. A 459, 1105–1115.Google Scholar
30. Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard–von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.Google Scholar
31. Rossiter, J. E. 1962 The effect of cavities on the buffeting of aircraft. Royal Aircraft Establishment Tech. Mem. 754.Google Scholar
32. Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.CrossRefGoogle Scholar
33. Sipp, D. & Marquet, O. 2012 Characterization of noise amplifiers with global singular modes: the case of the leading-edge flat-plate boundary layer. Theor. Comput. Fluid. Dyn. doi:10.1007/s00162-012-0265-y.Google Scholar
34. Sipp, D., Marquet, O., Meliga, O. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open flows: a linearized approach. Appl. Mech. Rev. 63, 030801.Google Scholar
35. Stanek, M. J., Visbal, M. R., Rizzetta, D. P., Rubin, S. G. & Khosla, P. K. 2007 On a mechanism of stabilizing turbulent free shear layers in cavity flows. Comput. Fluids 36, 1621–1637.CrossRefGoogle Scholar
36. Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex shedding at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
37. Wiltse, J. M. & Glezer, A. 1998 Direct excitation of small-scale motions in free shear flows. Phys. Fluids 10 (8), 2026–2036.Google Scholar

Sipp supplementary movie

DNS at Re= 6250. Control has been switched on at t= 92.2 and is characterized by ω_f=13. In the animation, we show the vorticity of the flowfield. The unstable global mode is stabilized.

Download Sipp supplementary movie(Video)
Video 951.5 KB

Sipp supplementary movie

DNS at Re= 6250. Control has been switched on at t= 92.2 and is characterized by ω_f=13. In the animation, we show the vorticity of the flowfield. The unstable global mode is stabilized.

Download Sipp supplementary movie(Video)
Video 6.5 MB