Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T19:47:45.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Onset of transient natural convection in porous media due to porosity perturbations

Published online by Cambridge University Press:  10 January 2018

Nils Tilton Open the ORCID record for Nils Tilton [Opens in a new window]
Nils Tilton*
Affiliation:
Department of Mechanical Engineering, Colorado School of Mines, Golden, CO 80401, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Onset of natural convection due to transient diffusion in porous media has attracted considerable attention for its applications to CO$_{2}$ sequestration. Stability analyses typically investigate the onset of such convection using an initial value problem approach in which a perturbation is introduced to the concentration field at an initial time 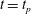$t=t_{p}$. This leads to debate concerning physically appropriate perturbations, the critical time 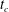$t_{c}$ for linear instability and the counter-intuitive notion of an optimal initial time 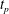$t_{p}$ that maximizes perturbation growth. We propose an alternate approach in which transient diffusion is continuously perturbed by small porosity variations. With this approach, instability occurs immediately (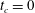$t_{c}=0$) without violating any physical constraints, such that the concepts of initial time 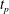$t_{p}$ and critical time 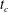$t_{c}$ become irrelevant. We also argue that the onset time for nonlinear convection is a more physically relevant parameter, and show that it can be predicted using a simple asymptotic expansion. Using the expansion, we explore the onset of nonlinear convection due to porosity perturbations that vary sinusoidally in the horizontal and vertical directions, and show there are optimal wavelengths that minimize the onset time. Finally, we find simple relationships for these wavelengths as functions of perturbation magnitude. These show that even small porosity perturbations, typically considered negligible in previous literature, are sufficient to trigger nonlinear convection and thereby influence the rate of CO$_{2}$ dissolution within time scales comparable to previous analyses.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection in porous media Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 838 , 10 March 2018 , pp. 129 - 147
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agartan, E., Trevisan, L., Cihan, A., Birkholzer, J., Zhou, Q. & Illangasekare, T. H. 2015 Experimental study on effects of geologic heterogeneity in enhancing dissolution trapping of supercritical CO2. Water Resour. Res. 51 (3), 1635–1648.Google Scholar
Aziz, K., Bories, S. A. & Combarnous, M. A. 1973 The influence of natural convection in gas, oil and water reservoirs. J. Can. Petrol. Technol. 2, 41–47.Google Scholar
Bear, J. 1972 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Ben, Y., Demekhin, E. A. & Chang, H.-C. 2002 A spectral theory for small-amplitude miscible fingering. Phys. Fluids 14, 999–1010.Google Scholar
Chen, J. C., Neitzel, G. P. & Jankowski, D. F. 1987 Numerical experiments on the stability of unsteady circular couette flow with random forcing. Phys. Fluids 30 (5), 1250–1258.Google Scholar
Daniel, D., Riaz, A. & Tchelepi, H. A. 2015 Onset of natural convection in layered aquifers. J. Fluid Mech. 767, 763781.Google Scholar
Daniel, D., Tilton, N. & Riaz, A. 2013 Optimal perturbations of gravitationally unstable, transient boundary layers in porous media. J. Fluid Mech. 727, 456–487.Google Scholar
De Wit, A. & Homsy, G. M. 1997 Viscous fingering in periodically heterogeneous porous media. I. Formulation and linear instability. J. Chem. Phys. 107 (22), 9609–9618.Google Scholar
Delfiner, P. 2007 Three statistical pitfalls of phi-k transforms. SPE Res. Evaluation Engng 10, 609–617.CrossRefGoogle Scholar
Doumenc, F., Boeck, T., Guerrier, B. & Rossi, M. 2010 Transient Rayleigh–Bénard–Marangoni convection due to evaporation: a linear non-normal stability analysis. J. Fluid Mech. 648, 521–539.Google Scholar
Elder, J. W. 1968 The unstable thermal interface. J. Fluid Mech. 32, 69–96.CrossRefGoogle Scholar
Ennis-King, J. & Paterson, L. 2003 Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. SPE 84344, 1–12.Google Scholar
Fernandez, J., Kurowski, P., Petitjeans, P. & Meiburg, E. 2002 Density-driven unstable flows of miscible fluids in a Hele-Shaw. J. Fluid Mech. 451, 239–260.Google Scholar
Foster, T. D. 1965 Stability of a homogeneous fluid cooled uniformly from above. Phys. Fluids 8, 1249–1257.CrossRefGoogle Scholar
Goldstein, A. W.1959 Stability of a horizontal fluid layer with unsteady heating from below and time-dependent body force. Tech. Rep. R-4. NASA Tech. Rep.Google Scholar
Goyal, N., Pichler, H. & Meiburg, E. 2007 Variable-density miscible displacements in a vertical Hele-Shaw cell: linear stability. J. Fluid Mech. 584, 357–372.Google Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2009 The effect of natural flow of aquifers and associated dispersion on the onset of buoyancy-driven convection in a saturated porous medium. AIChE J. 55, 475–485.CrossRefGoogle Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.Google Scholar
Jhaveri, B. S. & Homsy, G. M. 1982 The onset of convection in fluid layers heated rapidly in a time-dependent manner. J. Fluid Mech. 114, 251–260.Google Scholar
Kneafsey, T. J. & Pruess, K. 2010 Laboratory flow experiments for visualizing carbon dioxide-induced, density-driven brine convection. Trans. Porous Med. 82 (1), 123–139.Google Scholar
Liu, H.-H., Zhang, G., Yi, Z. & Wang, Y. 2013 A permeability-change relationship in the dryout zone for CO2 injection into saline aquifers. Intl J. Greenh. Gas Control 15, 42–47.Google Scholar
Nayfeh, A. H. 1981 Introduction to Perturbation Techniques. Wiley.Google Scholar
Neitzel, G. P., Kirkconnell, C. S. & Little, L. J. 1995 Transient, nonaxisymmetric modes in the instability of unsteady circular couette flow. Laboratory and numerical experiments. Phys. Fluids 7 (2), 324–334.Google Scholar
Nomeli, M. A., Tilton, N. & Riaz, A. 2014 A new model for the density of staurated solutions of CO2 -H2 0-NaCl in saline aquifers. Intl J. Greenh. Gas Control 31, 192–204.Google Scholar
Outeda, R., El Hasi, C., D’Onofrio, A. & Zalts, A. 2014 Experimental study of linear and nonlinear regimes of density-driven instabilities induced by CO2 dissolution in water. Chaos 24 (1), 013135.Google Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in CO2 storage in saline aquifers. Adv. Water Resour. 33, 443–455.CrossRefGoogle Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flows. Springer.Google Scholar
Rapaka, S., Chen, S., Pawar, R. J., Stauffer, P. H. & Zhang, D. 2008 Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech. 609, 285–303.Google Scholar
Riaz, A. & Cinar, Y. 2014 Carbon dioxide sequestration in saline formations: part i review of the modeling of solubility trapping. J. Petrol. Sci. Engng 124, 367–380.CrossRefGoogle Scholar
Riaz, A., Hesse, M., Tchelepi, A. & Orr, F. M. 2006 Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.Google Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids 25, 024101.Google Scholar
Slim, A. C. & Ramakrishnan, T. S. 2010 Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids 22, 124103.Google Scholar
Tan, C. T. & Homsy, G. M. 1988 Simulation of nonlinear viscous fingering in miscible displacement. Phys. Fluids 31 (6), 1330–1338.Google Scholar
Tang, T. & Mcdonough, J. M. 2016 A theoretical model for the porosity permeability relationship. Intl J. Heat Mass Transfer 103, 984–996.Google Scholar
Tilton, N., Daniel, D. & Riaz, A. 2013 The initial transient period of gravitationally unstable diffusive boundary layers developing in porous media. Phys. Fluids 25, 092107.CrossRefGoogle Scholar
Tilton, N. & Riaz, A. 2014 Nonlinear stability of gravitationally unstable transient boundary layers in porous media. J. Fluid Mech. 745, 251–278.Google Scholar
Verma, A. & Pruess, K. 1988 Thermohydrological conditions and silica redistribution near high-level nuclear wastes emplaced in saturated geological formations. J. Geophys. Res. 93 (B2), 1159–1173.Google Scholar
Vreme, A., Nadal, F., Pouligny, B., Jeandet, P., Liger-Belair, G. & Meunier, P. 2016 Gravitational instability due to the dissolution of carbon dioxide in a Hele-Shaw cell. Phys. Rev. Fluids 1, 064301.Google Scholar
Whitaker, S. 1999 The Method of Volume Averaging. Kluwer Academic Publishers.CrossRefGoogle Scholar
Wooding, R. A., Tylers, S. W. & White, I. 1997 Convection in groundwater below an evaporating salt lake: 1. Onset of instability. Water Resour. Res. 33, 1199–1217.Google Scholar