Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T11:33:47.327Z Has data issue: false hasContentIssue false
  • English
  • Français

On triadic resonance as an instability mechanism in precessing cylinder flow

Published online by Cambridge University Press:  27 February 2018

Thomas Albrecht Open the ORCID record for Thomas Albrecht [Opens in a new window] ,
Hugh M. Blackburn ,
Juan M. Lopez Open the ORCID record for Juan M. Lopez [Opens in a new window] ,
Richard Manasseh  and
Patrice Meunier Open the ORCID record for Patrice Meunier [Opens in a new window]
Thomas Albrecht*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
Hugh M. Blackburn
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
Juan M. Lopez
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe, AZ 85287, USA
Richard Manasseh
Affiliation:
Department of Mechanical and Product Design Engineering, Swinburne University of Technology, VIC 3122, Australia
Patrice Meunier
Affiliation:
IRPHE, CNRS, Aix–Marseille Université, Centrale Marseille, 49 Rue Joliot-Curie, 13013 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Contained rotating flows subject to precessional forcing are well known to exhibit rapid and energetic transitions to disorder. Triadic resonance of inertial modes has been previously proposed as an instability mechanism in such flows, and that idea was developed into a successful model for predicting instability in a cylindrical container when departures from solid-body rotation are sufficiently small. Using direct numerical simulation and dynamic mode decomposition, we analyse instabilities of precessing cylinder flows whose three-dimensional basic states, steady in the gimbal frame of reference, may depart substantially from solid-body rotation. In the gimbal frame, the instability can be interpreted as resulting from a supercritical Hopf bifurcation that results in a limit-cycle flow. In the cylinder frame of reference, the basic state is a rotating wave with azimuthal wavenumber 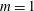$m=1$, and the instability satisfies triadic-resonance conditions with the instability mode maintaining a fixed orientation with respect to the basic state. Thus, we are able to demonstrate the existence of two alternative but congruent explanations for the instability. Additionally, we show that basic states may depart substantially from solid-body rotation even with modest cylinder tilt angles, and growth rates for instabilities may be sufficiently large that nonlinear saturation to disordered states can occur within approximately ten cylinder revolutions, in agreement with experimental observations.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Instability: Transition to turbulence Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 841 , 25 April 2018 , R3
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Brandt, L., Henningson, D. S., Hœpfner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions to the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 068102.CrossRefGoogle Scholar
Albrecht, T., Blackburn, H. M., Lopez, J. M., Manasseh, R. & Meunier, P. 2015 Triadic resonances in precessing rapidly rotating cylinder flows. J. Fluid Mech. 778, R1.CrossRefGoogle Scholar
Albrecht, T., Blackburn, H. M., Meunier, P., Manasseh, R. & Lopez, J. M. 2016 Experimental and numerical investigation of a strongly-forced precessing cylinder flow. Intl J. Heat Fluid Flow 61, 68–74.CrossRefGoogle Scholar
Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.Google Scholar
Eloy, C., Le Gal, P. & Le Dizés, S. 2003 Elliptic and triangular instabilities in rotating cylinders. J. Fluid Mech. 476, 357–388.CrossRefGoogle Scholar
Giesecke, A., Albrecht, T., Gundrum, T., Herault, J. & Stefani, F. 2015 Triadic resonances in nonlinear simulations of a fluid flow in a precessing cylinder. New J. Phys. 17, 113044.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Horn, S. & Schmid, P. J. 2017 Prograde, retrograde, and oscillatory modes in rotating Rayleigh–Bénard convection. J. Fluid Mech. 831, 182–211.CrossRefGoogle Scholar
Jovanović, M. R., Schmid, P. J. & Nichols, J. W. 2014 Sparsity-promoting dynamic mode decomposition. Phys. Fluids 26 (2), 024103.Google Scholar
Kerswell, R. R. 1993 The instability of precessing flow. Geophys. Astrophys. Fluid Dyn. 72, 107–144.Google Scholar
Kerswell, R. R. 1999 Secondary instabilities in rapidly rotating fluids: inertial wave breakdown. J. Fluid Mech. 382, 283–306.Google Scholar
Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34, 83–113.Google Scholar
Lagrange, R., Eloy, C., Nadal, F. & Meunier, P. 2008 Instability of a fluid inside a precessing cylinder. Phys. Fluids 20, 081701.Google Scholar
Lagrange, R., Meunier, P., Nadal, F. & Eloy, C. 2011 Precessional instability of a fluid cylinder. J. Fluid Mech. 666, 104–145.Google Scholar
Lopez, J. M. & Marques, F. 2018 Rapidly rotating precessing cylinder flows: forced triadic resonances. J. Fluid Mech. 839, 239–270.Google Scholar
Malkus, W. V. R. 1968 Precession of the Earth as the cause of geomagnetism. Science 160, 259–264.Google Scholar
Malkus, W. V. R. 1989 An experimental study of the global instabilities due to the tidal (elliptical) distortion of a rotating elastic cylinder. Geophys. Astrophys. Fluid Dyn. 48, 123–134.Google Scholar
Manasseh, R. 1992 Breakdown regimes of inertia waves in a precessing cylinder. J. Fluid Mech. 243, 261–296.Google Scholar
Marques, F. & Lopez, J. M. 2015 Precession of a rapidly rotating cylinder flow: traverse through resonance. J. Fluid Mech. 782, 63–98.CrossRefGoogle Scholar
McEwan, A. D. 1970 Inertial oscillations in a rotating fluid cylinder. J. Fluid Mech. 40, 603–640.Google Scholar
Meunier, P., Eloy, C., Lagrange, R. & Nadal, F. 2008 A rotating fluid cylinder subject to weak precession. J. Fluid Mech. 599, 405–440.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Zhang, K. & Liao, X. 2017 Theory and Modeling of Rotating Fluids: Convection, Inertial Waves and Precession. Cambridge University Press.CrossRefGoogle Scholar

Albrecht et al. supplementary movie 1

Kalliroscopic flow visualizations of a `Type A collapse' at Re = 21120 from the experiments of Manasseh (1992). The movie commences after establishment of solid-body rotation in the cylinder, followed by tilting through α = 3°. At early times, the initial bright area that we associate with a vortex core is thought to arise from locally large spatial gradients of flake orientation and finite light sheet thickness.

Download Albrecht et al. supplementary movie 1(Video)
Video 27.2 MB

Albrecht et al. supplementary movie 2

100 snapshots of ± isosurfaces of axial vorticity as seen from the gimbal frame of reference, normalised such that Em=2 = 1 to remove exponential growth, and extracted from the interval 31.890 ≤ t/T1 ≤ 34.733 (cf. figure 3). The wave envelope remains steady with respect to the gimbal frame (and the basic state), but there is a dominant frequency associated with progress of the wave; this is the phase frequency of the wave in the gimbal frame (cf. figure 5,i>a).

Download Albrecht et al. supplementary movie 2(Video)
Video 1.6 MB

Albrecht et al. supplementary movie 3

As for movie 2, but visualised in the cylinder frame of reference. The whole wave as well as the basic state revolve at circular frequency Ω1 with respect to the observer.

Download Albrecht et al. supplementary movie 3(Video)
Video 3.9 MB