Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Saxton, M. A.
Vella, D.
Whiteley, J. P.
and
Oliver, J. M.
2017.
Kinetic effects regularize the mass-flux singularity at the contact line of a thin evaporating drop.
Journal of Engineering Mathematics,
Vol. 106,
Issue. 1,
p.
47.
Savva, Nikos
Rednikov, Alexey
and
Colinet, Pierre
2017.
Asymptotic analysis of the evaporation dynamics of partially wetting droplets.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
574.
Rednikov, A. Ye.
and
Colinet, P.
2017.
Asymptotic analysis of the contact-line microregion for a perfectly wetting volatile liquid in a pure-vapor atmosphere.
Physical Review Fluids,
Vol. 2,
Issue. 12,
Tran, Ha V.
Nguyen, Tuan A.H.
Biggs, Simon R.
and
Nguyen, Anh V.
2018.
On the predictions for diffusion-driven evaporation of sessile droplets with interface cooling.
Chemical Engineering Science,
Vol. 177,
Issue. ,
p.
417.
Jambon-Puillet, Etienne
Carrier, Odile
Shahidzadeh, Noushine
Brutin, David
Eggers, Jens
and
Bonn, Daniel
2018.
Spreading dynamics and contact angle of completely wetting volatile drops.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
817.
Kiradjiev, K. B.
Breward, C. J. W.
and
Griffiths, I. M.
2019.
Surface-tension- and injection-driven spreading of a thin viscous film.
Journal of Fluid Mechanics,
Vol. 861,
Issue. ,
p.
765.
Qin, Feifei
Del Carro, Luca
Mazloomi Moqaddam, Ali
Kang, Qinjun
Brunschwiler, Thomas
Derome, Dominique
and
Carmeliet, Jan
2019.
Study of non-isothermal liquid evaporation in synthetic micro-pore structures with hybrid lattice Boltzmann model.
Journal of Fluid Mechanics,
Vol. 866,
Issue. ,
p.
33.
Rednikov, A. Y.
and
Colinet, P.
2019.
Contact-line singularities resolved exclusively by the Kelvin effect: volatile liquids in air.
Journal of Fluid Mechanics,
Vol. 858,
Issue. ,
p.
881.
Savva, Nikos
Groves, Danny
and
Kalliadasis, Serafim
2019.
Droplet dynamics on chemically heterogeneous substrates.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
321.
Ye, Xuemin
Zhang, Xiangshan
Li, Minglan
Li, Chunxi
and
Dong, Shuai
2019.
Contact line dynamics of two-dimensional evaporating drops on heated surfaces with temperature-dependent wettabilities.
International Journal of Heat and Mass Transfer,
Vol. 128,
Issue. ,
p.
1263.
Groves, Danny
and
Savva, Nikos
2021.
Droplet motion on chemically heterogeneous substrates with mass transfer. I. Two-dimensional dynamics.
Physical Review Fluids,
Vol. 6,
Issue. 12,
Savva, Nikos
and
Groves, Danny
2021.
Droplet motion on chemically heterogeneous substrates with mass transfer. II. Three-dimensional dynamics.
Physical Review Fluids,
Vol. 6,
Issue. 12,
Benilov, E. S.
2021.
Can a liquid drop on a substrate be in equilibrium with saturated vapor?.
Physical Review E,
Vol. 104,
Issue. 3,
Benilov, E. S.
2022.
Capillary condensation of saturated vapor in a corner formed by two intersecting walls.
Physics of Fluids,
Vol. 34,
Issue. 6,
Ruiz Pestana, Luis
and
Head-Gordon, Teresa
2022.
Evaporation of Water Nanodroplets on Heated Surfaces: Does Nano Matter?.
ACS Nano,
Vol. 16,
Issue. 3,
p.
3563.
Benilov, E. S.
2022.
Dynamics of a drop floating in vapor of the same fluid.
Physics of Fluids,
Vol. 34,
Issue. 4,
Benilov, E.S.
2023.
The multicomponent diffuse-interface model and its application to water/air interfaces.
Journal of Fluid Mechanics,
Vol. 954,
Issue. ,
Yang, Lisong
Pahlavan, Amir A.
Stone, Howard A.
and
Bain, Colin D.
2023.
Evaporation of alcohol droplets on surfaces in moist air.
Proceedings of the National Academy of Sciences,
Vol. 120,
Issue. 38,
Benilov, E.S.
2023.
Does Maxwell's hypothesis of air saturation near the surface of evaporating liquid hold at all spatial scales?.
Journal of Fluid Mechanics,
Vol. 971,
Issue. ,
Hartmann, Simon
Diddens, Christian
Jalaal, Maziyar
and
Thiele, Uwe
2023.
Sessile drop evaporation in a gap – crossover between diffusion-limited and phase transition-limited regime.
Journal of Fluid Mechanics,
Vol. 960,
Issue. ,
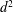 $d^{2}$-law valid?
$d^{2}$-law valid?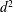 $d^{2}$-law. However, for a sufficiently large rate of evaporation, our analysis predicts that a (slightly different) ‘
$d^{2}$-law. However, for a sufficiently large rate of evaporation, our analysis predicts that a (slightly different) ‘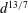 $d^{13/7}$-law’ is more appropriate. Our asymptotic results are validated by comparison with numerical simulations.
$d^{13/7}$-law’ is more appropriate. Our asymptotic results are validated by comparison with numerical simulations.


