On the wavenumber–frequency spectrum of the wall pressure fluctuations in turbulent channel flow

Abstract

Direct numerical simulations (DNS) of turbulent channel flows up to ${Re}_{\tau} \approx 1000$ are conducted to investigate the three-dimensional (consisting of streamwise wavenumber, spanwise wavenumber and frequency) spectrum of wall pressure fluctuations. To develop a predictive model of the wavenumber–frequency spectrum from the wavenumber spectrum, the time decorrelation mechanisms of wall pressure fluctuations are investigated. It is discovered that the energy-containing part of the wavenumber–frequency spectrum of wall pressure fluctuations can be well predicted using a similar random sweeping model for streamwise velocity fluctuations. To refine the investigation, we further decompose the spectrum of the total wall pressure fluctuations into the autospectra of rapid and slow pressure fluctuations, and the cross-spectrum between them. We focus on evaluating the assumption applied in many predictive models, that is, the magnitude of the cross-spectrum is negligibly small. The present DNS shows that neglecting the cross-spectrum causes a maximum error up to 4.7 dB in the subconvective region for all Reynolds numbers under test. Our analyses indicate that the approximation of neglecting the cross-spectrum needs to be applied carefully in the investigations of acoustics at low Mach numbers, in which the subconvective components of wall pressure fluctuations make important contributions to the radiated acoustic power.

1. Introduction

Wall pressure fluctuations are dominant sources of flow-generated noise in wall-bounded turbulence (Graham 1997; Wang, Freund & Lele 2006). The sound radiated by a solid wall depends on the intensity and spatial–temporal variations of the pressure fluctuations. Understanding the characteristics of the wavenumber–frequency spectrum of the wall pressure fluctuations is crucial for developing predictive models of flow-generated noise.

Experimental measurement (Corcos 1964; Blake 1970; Willmarth 1975; Farabee & Casarella 1991) is an important approach for acquiring data of wall pressure fluctuations. Arguillat et al. (2005) and Salze et al. (2014) used an array of sensors to measure the spatial correlations of wall pressure fluctuations at different frequencies, and applied Fourier transform in space to obtain the wavenumber–frequency spectrum. The energy-containing parts of the wavenumber–frequency spectrum, including the convective peak and acoustic part, were identified in their experiments, while other parts with lower energy level were unresolved.

Another approach for investigating the wall pressure fluctuations is numerical simulation. Kim (1989) pioneered the direct numerical simulation (DNS) study of pressure fluctuations in a turbulent channel flow at ${Re}_{\tau} =180$, with a focus on the root mean square (r.m.s.) profiles, one-dimensional (either wavenumber or frequency) spectra and also probability density functions. The database established by Kim (1989) was further analysed by Choi & Moin (1990) to investigate the wavenumber–frequency spectrum of wall pressure fluctuations. They identified the convective characteristic of wall pressure fluctuations, and showed that the similarity form of the spectrum proposed in an early study of Corcos (1964) was only accurate at small length and time scales. Chang III, Piomelli & Blake (1999) also conducted DNS of turbulent channel flow at ${Re}_{\tau} =180$ to study the wall pressure fluctuations. While Chang III et al. (1999) compared the magnitude of the source terms of the wall pressure fluctuations in different regions, Anantharamu & Mahesh (2020) systematically analysed the cross-spectral density between the source terms at two wall-normal locations. Anantharamu & Mahesh (2020) concluded that the dominant sources of the wall pressure fluctuations were located in the buffer layer. Hu, Morfey & Sandham (2002) used DNS data of turbulent channel flow at ${Re}_{\tau} =180$ to study the wavenumber–frequency spectrum of wall pressure fluctuations at low wavenumbers corresponding to large-scale turbulent motions. They argued that the wavenumber–frequency spectrum of wall pressure fluctuations showed no $k^2$-scaling at low wavenumbers as predicted theoretically by Kraichnan (1956) and Phillips (1956), where $k$ refers to the norm of the wavenumber vector consisting of streamwise and spanwise components. While the above DNS studies of pressure fluctuations are confined to ${Re}_{\tau} =180$, Abe, Matsuo & Kawanura (2005) conducted DNS of turbulent channel flows up to ${Re}_{\tau} \approx 1000$ to investigate the effect of Reynolds number on the pressure fluctuations. Hu, Morfey & Sandham (2006) analysed DNS data of turbulent channel flows from ${Re}_{\tau} =90$ to 1440 to investigate the scaling of the frequency spectrum of wall pressure fluctuations at different characteristic frequencies. Xu et al. (2020) derived a theoretical model of the streamwise-wavenumber spectrum of pressure fluctuations in the logarithmic layer based on Kolmogorov's theory (Kolmogorov 1941) and Townsend's attached eddy hypothesis (Townsend 1976). This model shows a good agreement with the DNS results in turbulent channel flows up to ${Re}_{\tau} =5200$ (Lee & Moser 2015). The above investigations of the pressure fluctuations at higher Reynolds numbers focused on their r.m.s. profiles and one-dimensional spectra, while owing to the requirements of long simulation times and large storage capacity, DNS investigations of the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations are limited to ${Re}_{\tau} =180$ (Choi & Moin 1990; Hu et al. 2002). Besides the above DNS studies, large-eddy simulations (LES) were also conducted to investigate the wall pressure fluctuations, in recent years. Gloerfelt & Berland (2013) performed LES of compressible turbulent boundary layer flow, which resolved the acoustic part of the wavenumber–frequency spectrum of wall pressure fluctuations. Viazzo, Dejoan & Schiestel (2001) and Park & Moin (2016) used both wall-resolved and wall-modelled LES to investigate the wavenumber–frequency spectrum of wall pressure fluctuations in turbulent channel flows.

Besides the experimental and numerical studies, numerous models were proposed to facilitate a fast prediction of the wavenumber–frequency spectrum of wall pressure fluctuations. To develop a model of the wavenumber–frequency spectrum (or equivalently, the space–time correlation in physical space), it is useful to understand the physical mechanisms of the time decorrelation process (He, Jin & Yang 2017). In previous studies of velocity fluctuations, it was discovered that in turbulent shear flows, the time decorrelation was mainly caused by the convection effect of mean flow (Taylor 1938) and the sweeping effect of large-scale turbulent eddies (Kraichnan 1964; Tennekes 1975). Models for space–time correlations (He & Zhang 2006; Zhao & He 2009) and wavenumber–frequency spectra (Wilczek & Narita 2012; Wilczek, Stevens & Meneveau 2015) of velocity fluctuations, which took both convection and sweeping into consideration, were proposed and tested. It was verified that the wavenumber–frequency spectra of velocity fluctuations obtained from these models were consistent with the DNS results in turbulent channel flows. By contrast, the time decorrelation mechanisms of wall pressure fluctuations were rarely investigated in the literature. In isotropic turbulence, Yao et al. (2008) showed analytically that the pressure fluctuations followed the same random advection equations of velocity fluctuations. However, in wall-bounded shear turbulence, time decorrelation mechanisms of wall pressure fluctuations have not been discussed in the literature, which are investigated using the present DNS data.

The DNS database is also useful for validating models. The existing models of wall pressure fluctuations can be categorized into two classes, namely the semiempirical models and those based on the Poisson equation of pressure fluctuations (Slama, Leblond & Sagaut 2018). In semiempirical models (e.g. Corcos 1964; Chase 1980, 1987; Smol'yakov 2006; Frendi & Zhang 2020), data fitting is usually used to directly construct the wavenumber–frequency spectrum of wall pressure fluctuations. Various semiempirical models predict similar spectral magnitudes around the convective peak, but show discrepancies at wavenumber–frequency combinations located in the subconvective region (which refers to the region in the wavenumber–frequency space with lower streamwise wavenumber than the convective peak). Detailed comparisons of different semiempirical models can be found in the review articles of Graham (1997) and Hwang, Bonness & Hambric (2009).

Different from the semiempirical models, the models based on the Poisson equation of the pressure fluctuations (e.g. Panton & Linebarger 1974; Peltier & Hambric 2007; Slama et al. 2018; Grasso et al. 2019) do not predict the wavenumber–frequency spectrum of wall pressure fluctuations directly. Instead, the wall pressure fluctuations are expressed as the solution of the following Poisson equation:

(1.1)\begin{equation} \frac{1}{\rho }{\nabla ^2}p ={-} 2\frac{{\partial {u_i}}}{{\partial {x_j}}} \frac{{\partial {U_j}}}{{\partial {x_i}}} - \frac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}({u_i}{u_j} - \langle {{u_i}{u_j}} \rangle ), \end{equation}

where $p$ denotes the pressure fluctuations, $\rho$ is the fluid density, $u_i$ and $U_i$ $(i=1, 2, 3)$ represent the velocity fluctuations and mean velocity, respectively, and a pair of angular brackets denotes averaging over time and the streamwise–spanwise plane. In (1.1), the right-hand side consists of a linear term and a quadratic term with respect to the velocity fluctuations $u_i$, which are called the rapid and slow source terms, respectively (Kim 1989). Because (1.1) is linear about the pressure fluctuations, the total pressure fluctuations can be decomposed into rapid and slow components, corresponding to the rapid and slow source terms, respectively. Thus, the wavenumber–frequency spectrum of the total wall pressure fluctuations can be decomposed into three components as the autospectra of rapid (AS-rapid) and slow (AS-slow) components, respectively, and the cross-spectrum between them (CS-RS). It is commonly assumed in the models based on the Poisson equation of pressure fluctuations that velocity fluctuations are Gaussian variables satisfying joint normal distributions (Peltier & Hambric 2007; Slama et al. 2018; Grasso et al. 2019). Because CS-RS is a cubic function of velocity fluctuations, it is neglected in these models, since odd-order moments of Gaussian variables are equal to zero, theoretically. In some semiempirical models, such as the Chase model (Chase 1980, 1987), this assumption is also applied. However, this assumption has not been confirmed by any numerical or experimental data.

In the present study, we conduct DNS of turbulent channel flows at four Reynolds numbers ranging from $Re_\tau =179$ to $998$ to investigate the characteristics of the wavenumber–frequency spectrum of wall pressure fluctuations. The objectives of the present study include the following. (1) To establish DNS database of the wavenumber–frequency spectrum of wall pressure fluctuations up to ${Re}_{\tau} \approx 1000$. (2) To investigate the time decorrelation mechanisms of wall pressure fluctuations. (3) To validate the assumption that CS-RS is negligibly small in comparison with AR-Rapid and AR-Slow. The remainder of this paper is organized as follows. Numerical details and the method to compute the wavenumber–frequency spectrum are described in § 2. The characteristics of the wavenumber–frequency spectrum of the total wall pressure fluctuations are analysed in § 3. The decorrelation mechanisms of wall pressure fluctuations are discussed in § 4. The decomposition of the wavenumber–frequency spectrum of wall pressure fluctuations is further investigated in § 5, followed by the conclusions in § 6.

2. Simulation parameters and numerical methods

Table 1 summarizes the key parameters of DNS. We have conducted DNS at four Reynolds numbers, $Re_\tau = u_\tau h / \nu = 179$, 333, 551 and 998, where $u_\tau =\sqrt {\tau _w/\rho }$ represents the wall-friction velocity, $h$ denotes one-half the channel height and $\nu$ is the kinematic viscosity. Here, $\tau _w$ is the mean wall shear stress, computed as

(2.1)\begin{equation} \tau_w=\frac{\tau_{w, low}+\tau_{w, up}}{2}=\frac{1}{2} \left(\mu\left.\frac{{\rm d} U}{{\rm d}y}\right|_{y={-}h}-\mu\left.\dfrac{{\rm d} U}{{\rm d}y}\right|_{y=h}\right), \end{equation}

where $\tau _{w,low}$ and $\tau _{w,up}$ are the mean wall stresses at the lower wall $y=-h$ and upper wall $y=h$, respectively, and $\mu =\rho \nu$ is the dynamic viscosity. The corresponding Reynolds numbers based on the bulk mean velocity $U_b$ are ${{Re}}_b=U_bh/\nu =2800$, 5700, 10 150 and 20 000, respectively. As mentioned in § 1, existing DNS results of the wavenumber–frequency spectrum of the wall pressure fluctuation are limited to a low Reynolds number, ${{Re}}_{\tau }=180$, in the literature (Choi & Moin 1990; Hu et al. 2002). In the present study, we conduct DNS at higher Reynolds numbers to further investigate the Reynolds number effects. The computational domain size is set to $L_x\times L_y\times L_z=4{\rm \pi} h\times 2h\times 2{\rm \pi} h$ in all cases. Hereinafter, the streamwise, wall-normal and spanwise directions are denoted using $x$, $y$ and $z$, respectively. The number of grid points $N_x\times N_y\times N_z$ is chosen to match the grid resolution of Hoyas & Jiménez (2006). Specifically, in the streamwise and spanwise directions, the grid resolution is set to ${\rm \Delta} x^+\approx 11$ and ${\rm \Delta} z^+\approx 5.5$, respectively. In this paper, the superscript ‘$+$’ denotes variables non-dimensionalized using the wall units $\nu /u_\tau$ and $u_\tau$ as characteristic length and velocity scales, respectively. The wall-normal grids are located on the Chebyshev collocation points, and the number of wall-normal grid points is similar to Hoyas & Jiménez (2006). The smallest spatial scales are comparable to the local Kolmogorov scales, and owing to the high accuracy of the pseudospectral method used for conducting the DNS, the numerical dissipation is negligible (Hoyas & Jiménez 2006). The flow is driven by a streamwise pressure gradient, which is adjusted to sustain the bulk mean velocity to a constant. Periodic boundary conditions are applied in the streamwise and spanwise directions, while no-slip and no-penetration conditions are prescribed at the solid walls. As pointed out by Choi & Moin (1990), the use of the periodic boundary condition in the wall-parallel directions can induce a numerical artefact called the artificial acoustic. However, as is discussed in both Choi & Moin (1990) and the present study (§ 3.2), the influence of the artificial acoustic is confined at a few smallest wavenumbers, corresponding to large length scales. Increasing the computational domain can reduce the influence of the artificial acoustic. The wavenumber–frequency spectrum of wall pressure fluctuations around the convection line considered in § 4 is merely influenced by the artificial acoustic, while in § 5, we mainly focus on the maximum error that occurs out of the wavenumbers and frequencies influenced by the artificial acoustic. In this regard, the present computational domain size of $L_x = 4{\rm \pi} h$ is sufficient for the problems under investigation. The continuity and momentum equations for incompressible flows are solved using an in-house pseudospectral-method code. Velocity and pressure are expanded into Fourier series in the streamwise and spanwise directions, and into Chebyshev polynomials in the wall-normal direction. The nonlinear terms are calculated in physical space, and the 3/2 rule is used to remove the aliasing errors (Patterson & Orszag 1971; Kim, Moin & Moser 1987). The third-order time splitting method of Karniadakis, Israeli & Orszag (1991) is used for time advancement. The computational time step is chosen to satisfy the Courant–Friedrichs–Lewy condition, which is ${\rm \Delta} t^+ = 0.057$, 0.039, 0.030, 0.040 for $Re_\tau = 179$, 333, 551, 998, respectively. The DNS code has been tested systematically in previous studies (Deng & Xu 2012; Deng, Huang & Xu 2016). Figure 1 compares the profiles of the mean velocity and Reynolds stresses $\langle uu\rangle ^+$, $\langle vv\rangle ^+$, $\langle ww\rangle ^+$, $\langle uv\rangle ^+$ of cases CH180 and CH1000 with the DNS results of Hoyas & Jiménez (2006) and Lee & Moser (2015). It is seen that the present results are in good agreement with the results in the literature.

Figure 1. Profiles of (a) mean velocity at ${{Re}}_{\tau }=179$, (b) mean velocity at ${{Re}}_{\tau }=998$, (c) Reynolds stresses at ${{Re}}_{\tau }=179$ and (d) Reynolds stresses at ${{Re}}_{\tau }=998$. The solid lines represent the results of the present DNS. The symbols in (a,c) denote the DNS results of Hoyas & Jiménez (2006) at $Re_\tau = 180$, while those in (b,d) denote the DNS results of Lee & Moser (2015) at $Re_\tau = 1000$. The dash–dotted lines in (a,b) represent the linear law $U^+=y^+$ and the dashed line in (b) represents the logarithmic law $U^+=\log y^+/\kappa +B$, where $\kappa = 0.384$ and $B=4.27$ are constants (Lee & Moser 2015).

Table 1. Key parameters of DNS, including the Reynolds numbers $Re_b$ and $Re_\tau$, computational domain size $L_x\times L_y\times L_z$, number of grid points $N_x\times N_y\times N_z$, grid resolution ${\rm \Delta} x^+\times {\rm \Delta} y^+\times {\rm \Delta} z^+$ and the time separation $T_s^+$ of data storage.

Once the turbulence is fully developed to a statistically stationary state, the instantaneous flow fields are stored with a time separation of $T_s^+$, ranging from 0.35 to 0.60 at different Reynolds numbers (see table 1). Since $T_s$ determines the largest resolved frequency, it should satisfy $T_s\le {\rm \Delta} x/U_{bc}$ in order to resolve the energy-containing convection line, where $U_{bc}$ is the bulk convection velocity (defined later in § 5.3). The above criterion is satisfied in all test cases. The wavenumber–frequency spectrum of wall pressure fluctuations is then calculated using the method described by Choi & Moin (1990). The time series of wall pressure fluctuations $p(x,z,t)$ are divided into $M$ intervals with 50 % overlapping between two neighbouring intervals. Each interval contains $N_t=512$ successive snapshots. A Fourier transform is then performed over the wall pressure fluctuation in each time interval in the streamwise and spanwise directions and in time to obtain the Fourier modes as

(2.2)\begin{align} \hat p({k_x},{k_z};\omega ) &= \frac{1}{{{L_x}{L_z}\sqrt {T\int_0^T {w{{(t)}^2}\,{\rm{d}}t} } }} \nonumber\\ &\quad \times\int_0^T {{\rm{d}}t\int_0^{{L_x}} {{\rm{d}}\kern0.7pt x \int_0^{{L_z}} {{\rm{d}}z \cdot w(t)p(x,z;t){\exp({-{\rm{i}}(x{k_x} + z{k_z} - \omega t)})}} } }, \end{align}

where $T=N_t\cdot T_s$ is the time duration of each interval and $w(t)$ is a standard Hanning window. Since all the DNS data are calculated on discrete grids, practically the discrete Fourier transform is used to compute $\hat p(k_x,k_z;\omega )$ as

(2.3)\begin{align} \hat p({k_x},{k_z};\omega ) &= \frac{\sqrt {8/3}}{{{N_x}{N_z}{N_t}}} \sum_{l=0}^{N_x-1}\sum_{m=0}^{N_z-1}\sum_{n=0}^{N_t-1}w \left(\frac{nT}{N_t}\right)p\left(\frac{lL_x}{N_x},\frac{mL_z}{N_z},\frac{nT}{N_t}\right)\nonumber\\ &\quad \times\exp({- {\rm{i}}(lL_x{k_x}/N_x + mL_z{k_z}/N_z - nT\omega/N_t)}), \end{align}

where a coefficient $\sqrt {8/3}$ is included to keep the r.m.s. value of $p$ unchanged after applying the window function $w(t)$. The wavenumber–frequency spectrum of wall pressure fluctuations is then calculated as

(2.4)\begin{equation} {\phi _{pp}}({k_x},{k_z},\omega ) = \frac{{\overline {\hat p({k_x},{k_z},\omega ){{\hat p}^*} ({k_x},{k_z},\omega )} }}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z}{\rm \Delta} \omega }}, \end{equation}

where ${\rm \Delta} k_x=2{\rm \pi} /L_x$ and ${\rm \Delta} k_z=2{\rm \pi} /L_z$ represent the streamwise- and spanwise- wavenumber resolution, respectively, and ${\rm \Delta} \omega =2{\rm \pi} /T$ is the frequency resolution. The overbar denotes time averaging over all of the $M$ intervals. In this paper, the results for $M=38$ are presented. To be specific, 5120 fields are stored for each case. These fields are then divided into 19 windows of 512 fields with 50 % overlap, and averaging over two walls doubles the number of samples $M$ to 38. The corresponding total time duration is 16.3, 6.0, 2.8 and 3.1 eddy turnover time ($h/u_{\tau }$) for ${{Re}}_{\tau }=179$, 333, 551 and 998, respectively. Because the windows are not randomly chosen, it is desired that the time duration of the data set for time averaging is sufficiently long. To verify this, we have conducted a data convergence analysis by changing the number of averaging samples $M$. The results are provided in the Appendix (A). It is seen that reducing the value of $M$ from 38 to 19 does not cause any qualitative change in the main conclusions of this paper.

The mean-square wall pressure fluctuation can be calculated as the summation of the discrete three-dimensional wavenumber–frequency spectrum over all spatial and temporal scales as

(2.5)\begin{equation} \overline{p^2} = \sum_{l={-}N_x/2}^{N_x/2-1}\sum_{m={-}N_z/2}^{N_z/2-1} \sum_{n={-}N_t/2}^{N_t/2-1}\phi_{pp}(l{\rm \Delta} k_x,m{\rm \Delta} k_z,n{\rm \Delta}\omega) {\rm \Delta} k_x{\rm \Delta} k_z{\rm \Delta} \omega. \end{equation}

Similarly, the reduced-dimension spectra are calculated by integrating the three- dimensional wavenumber–frequency spectrum given by (2.4). For example, the one-dimensional streamwise-wavenumber spectrum $\phi _{pp}(k_x)$ is the integration of $\phi _{pp}(k_x,k_z,\omega )$ over the spanwise wavenumber $k_z$ and frequency $\omega$.

3. The wavenumber–frequency spectrum of the total wall pressure fluctuations

The wavenumber–frequency spectrum of wall pressure fluctuations is a key input of predictive models of turbulent-generated noise. In the literature, DNS investigations of the wavenumber–frequency spectrum of wall pressure fluctuations are limited to ${Re}_{\tau} =180$. In this section, we analyse the DNS results of the wavenumber–frequency spectrum of the total wall pressure fluctuations up to ${Re}_{\tau} =998$.

3.1. One-dimensional spectra

We start our results analyses with the one-dimensional spectra. We note that the one-dimensional spectra of the wall pressure fluctuation have been previously studied (Abe et al. 2005; Anantharamu & Mahesh 2020). The purpose of presenting the results of the one-dimensional spectra is to provide a further validation of our DNS data.

Figure 2 compares the one-dimensional streamwise-wavenumber spectrum, spanwise- wavenumber spectrum and frequency spectrum of the wall pressure fluctuation at various Reynolds numbers. The spectra are non-dimensionalized using the wall units. To validate our results, the one-dimensional spectra of wall pressure fluctuations at ${Re}_{\tau} =180$ calculated by Choi & Moin (1990) are superposed. The present results for case CH180 are in good agreement with the results of Choi & Moin (1990). All of the one-dimensional spectra at different Reynolds numbers are close to each other at high wavenumbers and high frequencies, indicating that the spectra are scaled by the wall units (Farabee & Casarella 1991; Hu et al. 2006; Hwang et al. 2009). At small wavenumbers or frequencies, the magnitudes of all one-dimensional spectra increase monotonically with the Reynolds number, an observation that agrees with the DNS results of Abe et al. (2005). Figures 2(a) and 2(c) show that as the streamwise wavenumber $k_x$ or frequency $\omega$ increases, the magnitude of the corresponding one-dimensional spectrum first increases, and then decreases. However, as depicted in figure 2(b), the magnitude of the one-dimensional spanwise-wavenumber spectrum $\phi _{pp}(k_z)$ decreases monotonically as $k_z$ increases.

Figure 2. One-dimensional spectra of wall pressure fluctuations at ${Re}_{\tau} =179$, 333, 551 and 998 with respect to (a) streamwise-wavenumber, (b) spanwise-wavenumber and (c) frequency. All spectra are non-dimensionalized using wall units. The results of Choi & Moin (1990) at ${Re}_{\tau} =180$ are shown for comparison.

3.2. Two-dimensional spectra

In this subsection, we analyse the two-dimensional spectra. To keep the paper concise, we focus on the results at ${Re}_{\tau} =998$. Figures 3(a) and 3(b) show the contours of the two-dimensional $k_x$–$\omega$ and $k_x$–$k_z$ spectra of the wall pressure fluctuation $\phi _{pp}$, respectively. For comparison, the contours of the $k_x$–$\omega$ and $k_x$–$k_z$ spectra of the streamwise velocity fluctuation $\phi _{uu}$ at $y^+=15$ are plotted in figures 3(c) and 3(d), respectively. We note that the $k_x$–$\omega$ spectra are symmetric about $(k_x,\omega ) = (0,0)$ and the $k_x$–$k_z$ spectra are symmetric about both $k_x=0$ and $k_z=0$. Therefore, only spectra at $k_x\ge 0$ are plotted in figure 3. As shown in figures 3(a) and 3(c), large magnitudes of $\phi _{pp}(k_x,\omega )$ and $\phi _{uu}(k_x,\omega )$ occur around their convection lines $\omega /k_x=U_{bc}$, demarcated using the dash–dotted lines. Here, the bulk convection velocity $U_{bc}$ is defined as (del Álamo & Jiménez 2009)

(3.1)\begin{equation} {U_{bc}} = \frac{{\int {\int {{k_x}\omega \phi ({k_x},\omega )\,{\rm d}\omega \,{\rm d}{k_x}} } }}{{\int {\int {k_x^2\phi ({k_x},\omega )\,{\rm d}\omega \,{\rm d}{k_x}} } }}, \end{equation}

where $\phi (k_x,\omega )$ represents the $k_x$–$\omega$ spectrum of either wall pressure fluctuations or velocity fluctuations. The values of the bulk convection velocity for wall pressure fluctuations ($u_{bc}^{+}=11.6$) and streamwise velocity fluctuations at $y^+=15$ ($u_{bc}^{+}=10.7$) are close to each other, indicating that the convection property of wall pressure fluctuations is similar to the velocity fluctuations in the buffer layer. This is consistent with the conclusion of Anantharamu & Mahesh (2020) that the velocity gradients in the buffer layer are the dominant sources of wall pressure fluctuations.

Figure 3. Isopleths of two-dimensional spectra of wall pressure fluctuations at $y^+ = 0$ and streamwise velocity fluctuations at $y^+=15$. (a) The $k_x$–$\omega$ spectrum of wall pressure fluctuations $\phi _{pp}(k_x,\omega )$; (b) $k_x$–$k_z$ spectrum of wall pressure fluctuations $\phi _{pp}(k_x,k_z)$; (c) $k_x$–$\omega$ spectrum of streamwise velocity fluctuations $\phi _{uu}(k_x,\omega )$; and (d) $k_x$–$k_z$ spectrum of streamwise velocity fluctuations $\phi _{uu}(k_x,k_z)$. The Reynolds number is ${Re}_{\tau} =998$.

Another important observation from figure 3(a) is that as $k_x$ approaches zero, the isopleths gradually contract towards $(k_x,\omega )=(0,0)$, especially at the energy-containing scales (see the two innermost isopleths of $\phi _{pp}(k_x,\omega )=10^{-4}$ and $10^{-5}$). This contracting feature is not observed from the isopleths of $\phi _{uu}(k_x,\omega )$, which are approximately parallel to the convection line at low streamwise wavenumbers. Similar contracting isopleths also appear in the $k_x$–$k_z$ spectrum of wall pressure fluctuations $\phi _{pp}(k_x,k_z)$ as shown in figure 3(b), but are absent for $\phi _{uu}(k_x,k_z)$ in figure 3(d). This contracting behaviour suggests that as $k_x$ increases from zero, the spectrum of wall pressure fluctuations first increases in a small range before it decreases. Such a non-monotonic behaviour is consistent with the one-dimensional spectrum $\phi _{pp}(k_x)$ plotted in figure 2(a). Later in § 5.3, we will further show that this contracting behaviour is correlated to the rapid pressure fluctuations.

3.3. The three-dimensional spectrum

In this section, we continue to analyse the three-dimensional spectrum $\phi _{pp}(k_x,k_z,\omega )$ of wall pressure fluctuations at $Re_\tau =998$. The variation of $\phi _{pp}(k_x,k_z,\omega )$ with respect to $k_x$ corresponding to $k_z=0$ and five frequencies $\omega h/u_\tau =123$, 245, 409, 573 and 716 is plotted in figure 4(a), while figure 4(b) shows the variation of $\phi _{pp}(k_x,k_z,\omega )$ as a function of $k_z$ for $k_x=0$ and the same five frequencies. Convective peaks (denoted by the filled circles) can be identified in all of the five lines in figure 4(a). As the frequency $\omega$ increases, the location of the convective peak moves to a higher streamwise wavenumber. Focusing on each profile, as the streamwise wavenumber $k_x$ decreases from the convective wavenumber to zero, the value of the $\phi _{pp}(k_x,k_z,\omega )$ first decreases, and then increases slightly at low streamwise wavenumbers, forming a weak local maximum at the lowest resolved streamwise wavenumber. This local maximum is identified as an artificial acoustic mode by Choi & Moin (1990), which is a numerical artefact induced by the periodic boundary condition imposed in the streamwise direction. It is seen from figure 4(a) that for $\omega h/u_\tau =123$, the artificial acoustic mode only appears at the lowest resolved streamwise wavenumber $k_xh=0.5$. The range of the streamwise wavenumber influenced by the artificial acoustic mode becomes larger as the frequency increases, but is still confined in a small neighbouring region around the lowest resolved streamwise wavenumber. Similarly, artificial acoustic modes also occur in the spanwise direction but are confined to small spanwise wavenumbers as shown in figure 4(b).

Figure 4. Three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations at specific wavenumbers and frequencies: (a) $k_z=0$ and (b) $k_x=0$. The five lines in (a,b) correspond to five frequencies $\omega h/u_\tau =123$, 245, 409, 573 and 716. The arrow points to the increasing direction of the frequency. The convective peaks are marked using filled circles in (a). The Reynolds number is $Re_\tau = 998$.

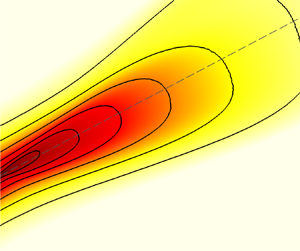
Figures 5(a) and 5(b) show the contours of $\phi _{pp}(k_x, k_z, \omega )$ corresponding to $\omega h/u_\tau =245$ and 716, respectively. Convective peaks can be identified for both frequencies (denoted by the cross symbols in figure 5), and the spectral value decays as the wavenumber moves away from the convective peaks. The isopleths are closed, ellipse-like curves, except for a small region near $(k_x,k_z)=(0,0)$. Owing to the artificial acoustic modes, the value of $\phi _{pp}(k_x, k_z, \omega )$ obtained from DNS does not decay to zero at $(k_x,k_z)=(0,0)$. To facilitate a clearer observation near $(k_x,k_z)=(0,0)$, figure 5(c) displays a zoom-in view of the dash–dotted box in figure 5(a). It is seen that the artificial acoustic modes only influence a small region around $(k_x,k_z)=(0,0)$ (marked by the red circle in figure 5c). Outside this circle, the isopleths form a ‘valley’ between $(k_x,k_z)=(0,0)$ and the convective peak. This observation shows the tendency that the magnitude of $\phi _{pp}(\boldsymbol {k},\omega )$ decays as the spanwise wavenumber approaches $k_z=0$ in the $k_x$–$k_z$ plane, which is in agreement with figure 4(b).

Figure 5. Contours of the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations $\phi _{pp}(k_x,k_z,\omega )$ in the $k_x$–$k_z$ plane for specific frequencies (a) $\omega h/u_\tau =245$ and (b) $\omega h/u_\tau =716$. Panel (c) shows a zoom-in view of the dash–dotted box region around $(k_x,k_z)=(0,0)$ in (a). The convective peaks are marked by the cross-symbols. In (c), the black dashed box denotes the area in which the isopleths form a valley, and the acoustic peak is located in the red circle. Note that in (a,b), the isopleth level ranges from $10^{-13}$ to $10^{-6}$, while in (c), it ranges from $10^{-11}$ to $10^{-5}$. The Reynolds number is $Re_\tau = 998$.

4. Time decorrelation mechanisms of wall pressure fluctuations

In previous studies of velocity fluctuations, the investigation of the time decorrelation mechanisms is found to be useful for developing predictive models of wavenumber– frequency ($k_x$–$\omega$) spectra (Wilczek & Narita 2012; Wilczek et al. 2015; He et al. 2017). However, the time decorrelation mechanisms of wall pressure fluctuations are rarely discussed in the literature. In this section, we examine if the frequency variation of the $k_x$–$\omega$ spectrum of wall pressure fluctuations follows the same functional form as that of velocity fluctuations.

As shown in figure 3(a), similar to the velocity fluctuations, the energy-containing region in the $k_x$–$\omega$ spectrum of wall pressure fluctuations is located around the convection line. This means that the convection by the mean flow is one of the main time decorrelation mechanisms of wall pressure fluctuations. On the other hand, the wavenumber–frequency spectrum is not concentrated exactly upon the convection line as predicted by Taylor's hypothesis (Taylor 1938). Instead, the energy-containing part distributes around the convection line, forming a finite bandwidth due to the Doppler broadening effect (Wu et al. 2017; Wu & He 2020). For velocity fluctuations, the Doppler broadening is caused by the large-scale sweeping effect (Kraichnan 1964; Tennekes 1975). To facilitate the investigation of the time decorrelation mechanisms of wall pressure fluctuations, we briefly review the linear random sweeping model of the wavenumber–frequency spectrum of streamwise velocity fluctuations proposed by Wilczek et al. (2015).

Considering an arbitrary variable $\psi$ (which is the streamwise velocity fluctuations $u$ in Wilczek et al. (2015)), in a turbulent channel flow, it is advected in the wall-parallel directions by both mean velocity $\boldsymbol {U}=(U,0)$ and large-scale sweeping velocity $\boldsymbol {v} = (v_x, v_z)$. The sweeping velocity is assumed to be a constant in space and time with a Gaussian ensemble (Kraichnan 1964; Yao et al. 2008; He et al. 2017). The spatial Fourier mode of $\psi$ follows a random advection equation:

(4.1)\begin{equation} \frac{\partial }{{\partial t}}\hat \psi (\boldsymbol{k},t) + {\rm i}(\boldsymbol{U} + \boldsymbol{v}) \boldsymbol{\cdot} \boldsymbol{k} \hat{\psi} (\boldsymbol{k},t) = 0. \end{equation}

The wavenumber–frequency spectrum of $\psi$ can be subsequently derived from the solution of (4.1) as (Wilczek et al. 2015)

(4.2)\begin{equation} \phi_{\psi\psi} (\boldsymbol{k},\omega ) = \phi_{\psi\psi} (\boldsymbol{k}) \boldsymbol{\cdot} \frac{1}{{\sqrt {2{\rm \pi} (\left\langle {v_x^2} \right\rangle k_x^2 + \left\langle {v_z^2} \right\rangle k_z^2)} }}\exp \left[ { - \frac{{{{(\omega - {k_x}U)}^2}}}{{2(\left\langle {v_x^2} \right\rangle k_x^2 + \left\langle {v_z^2} \right\rangle k_z^2)}}} \right]. \end{equation}

In (4.2), the wavenumber–frequency spectrum is estimated using the multiplication between the wavenumber spectrum $\phi _{\psi \psi } (\boldsymbol {k})$ and a Gaussian function of the frequency. The numerical results in Wilczek et al. (2015) showed that (4.2) accurately predicts the wavenumber–frequency spectrum of velocity fluctuations $\phi _{uu}$ in turbulent channel flows, especially at the energy-containing $k_x$–$\omega$ combinations along the convection line. This indicates that sweeping is also a main physical mechanism for the time decorrelation of velocity fluctuations in wall-bounded turbulence. In the rest of this section, we examine if the wavenumber–frequency spectrum of wall pressure fluctuations $\phi _{pp}(k_x,k_z,\omega )$ follows the same functional form as $\phi _{uu}(k_x,k_z,\omega )$.

Figure 6(a) compares the isopleths of $\phi _{pp}(k_x,\omega )$ obtained from DNS and (4.2). Here the convection velocity $U$ in (4.2) is chosen as the bulk convection velocity $U^+ = 11.6$. Wilczek et al. (2015) found that the r.m.s. sweeping velocities of the spectrum of streamwise velocity fluctuations can be well approximated by the local r.m.s. velocities. Because the velocity sources in the buffer layer contribute most to wall pressure fluctuations (Anantharamu & Mahesh 2020), we choose the r.m.s. velocities at $y^+=15$ as the r.m.s. sweeping velocities in model (4.2). As such, all the three velocities in this model are chosen as quantities with physical meanings related to wall pressure fluctuations, and no parameter needs to be adjusted in the following comparison. The model (4.2) is in good agreement with the DNS result in the energy-containing spatial–temporal scales. Specifically, the isopleths of $10^{-4}$ and $10^{-5}$ obtained from the model are almost coincident with the DNS result. The contracting feature at low streamwise wavenumbers is also well captured by the model. As is shown in § 5.3, the contracting feature is induced by the scaling of the rapid pressure at low streamwise wavenumbers. Because this scaling behaviour is a spatial property embedded in the wavenumber spectrum $\phi _{pp}(\boldsymbol {k})$ as a model input, it is also satisfied by the model of the wavenumber–frequency spectrum $\phi _{pp}(\boldsymbol {k}, \omega )$ given by (4.2). Figure 6(b) further shows three slices of $\phi _{pp}(k_x,\omega )$ at $k_x h = 20$, 70 and 150. For the two lower wavenumbers $k_xh = 20$ and 70, the frequency distributions of $\phi _{pp}(k_x,\omega )$ obtained from the model are close to the DNS results around the convective peaks. For the higher wavenumber $k_xh=150$, the convection peak predicted by the model shifts to a higher frequency in comparison with the DNS result. This indicates that the convection velocity is scale dependent, which is further investigated in § 5.3. We have tested that, if a scale-dependent convection velocity $U(k_x)$ is used in model (4.2), then the peak locations predicted by the model also match the DNS results at high wavenumbers. Since the present model mainly focuses on the energy-containing scales, we choose a constant convection velocity in the model to keep it simple. Furthermore, the model spectrum decreases faster than the DNS result at low and high wavenumbers away from the convective peak. This is because the model assumes a Gaussian decay at all frequencies, while the DNS spectrum indeed shows an approximately exponential decay at high frequencies.

Figure 6. The wavenumber–frequency spectrum of wall pressure fluctuations $\phi _{pp}(k_x,\omega )$ obtained from DNS and from model (4.2). (a) Contours in the $k_x$–$\omega$ plane. (b) Variation of $\phi _{pp}(k_x,\omega )$ with respect to the dimensionless frequency $\omega h / u_\tau$ for specific streamwise wavenumbers $k_x h = 20$, 70 and 150. In (a,b), the solid and dashed lines represents DNS and model results, respectively. The Reynolds number is $Re_\tau = 998$.

To further show the capability of (4.2) in the prediction of the energy-containing part of wavenumber–frequency spectrum of wall pressure fluctuations, we define the following indicator function $I$ as the ratio between the spectra obtained from the model and DNS:

(4.3)\begin{equation} {I} = \frac{\phi_{pp,model}(\boldsymbol{k},\omega)}{\phi_{pp,DNS}(\boldsymbol{k},\omega)}. \end{equation}

If the wavenumber–frequency spectrum of wall pressure fluctuations follows the functional form of (4.2), then the value of $I$ should be equal to unity. Figures 7(a) and 7(b) depict the variation of $I$ with respect to the frequency $\omega$ for $k_z=0$ and $k_x=0$, respectively. It is observed that plateaus with $I = 1$ exist in the energy-containing scales in both figures 7(a) and 7(b). This indicates that the wavenumber–frequency spectrum of wall pressure fluctuations follows the random sweeping model (4.2) at energy-containing scales. Similar to the velocity fluctuations, the Doppler broadening effect on the wavenumber–frequency spectrum of wall pressure fluctuations is also induced by the large-scale random sweeping. Noticing that the wall pressure fluctuations can be expressed as an integration of the source terms weighted by the Green's function (Kim 1989), the time decorrelation properties of wall pressure fluctuations can be regarded as the weighted average properties of the velocity source terms. Thus, it is reasonable that the wavenumber–frequency spectrum of wall pressure fluctuations has the similar functional form as velocity fluctuations.

Figure 7. Variation of the indicator function $I$ for the spectrum of wall pressure fluctuations obtained from the random sweeping model with respect to the dimensionless frequency $\omega h / u_\tau$ for specific wavenumbers: (a) $k_z=0$ and $k_x = 100$, 120, 140, 160, 180 and 200; (b) $k_x=0$ and $k_z=100$, 120, 140, 160, 180 and 200. The arrow points to the increasing direction of the streamwise or spanwise wavenumber. The horizontal dashed lines denote $I=1$. The Reynolds number is $Re_\tau = 998$.

5. Decomposition of the wavenumber–frequency spectrum of wall pressure fluctuations

5.1. Mathematical description of the decomposition

According to (1.1), the pressure fluctuations can be decomposed into two components as

(5.1)\begin{equation} p = p_r + p_s. \end{equation}

The rapid pressure fluctuations $p_r$ and slow pressure fluctuations $p_s$ are governed by the following Poisson equations:

(5.2)\begin{equation} \left. \begin{array}{l@{}} \displaystyle {{\nabla ^2}{p_r} = {f_r} ={-} 2\rho\dfrac{{\partial {u_i}}}{{\partial {x_j}}} \dfrac{{\partial {U_j}}}{{\partial {x_i}}}}, \\ \displaystyle {{\nabla ^2}{p_s} = {f_s} ={-} \rho\dfrac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}({u_i}{u_j} - \overline {{u_i}{u_j}} )}, \end{array} \right\} \end{equation}

respectively, where $f_r$ and $f_s$ denote the corresponding source terms. Because the magnitude of the Stokes pressure induced by the inhomogeneous boundary condition becomes increasingly small as the Reynolds number increases (Gerolymos, Sénéchal & Vallet 2013), we adopt the homogeneous Neumann boundary conditions ${{\partial {p_r}/\partial y} |_{y = \pm h}} = {{\partial {p_s}/\partial y} |_{y = \pm h}} = 0$ for both rapid and slow pressure fluctuations following Anantharamu & Mahesh (2020). Performing a Fourier transform over (5.2) results in the following Helmholtz equations:

(5.3)\begin{equation} \left. \begin{array}{l@{}} \displaystyle {\dfrac{{\partial^2 {{\hat p}_r}(\boldsymbol{k},\omega ;y)}}{{\partial {y^2}}} - {k^2}{{\hat p}_r}(\boldsymbol{k},\omega ;y) = {{\hat f}_r}(\boldsymbol{k},\omega ;y)},\quad {\partial {{\hat p}_r}/\partial y{{\rm{|}}_{y ={\pm} h}} = 0}, \\ \displaystyle {\dfrac{{\partial^2 {{\hat p}_s}(\boldsymbol{k},\omega ;y)}}{{\partial {y^2}}} - {k^2}{{\hat p}_s}(\boldsymbol{k},\omega ;y) = {{\hat f}_s}(\boldsymbol{k},\omega ;y)},\quad {\partial {{\hat p}_s}/\partial y{{\rm{|}}_{y ={\pm} h}} = 0}, \end{array} \right\} \end{equation}

where ${\hat p_r}$, ${\hat p_s}$, ${\hat f_r}$ and ${\hat f_s}$ denote the Fourier modes of ${p_r}$, ${p_s}$, ${f_r}$ and ${f_s}$, respectively. The solution of (5.3) can be expressed as an integration of the source term $\hat f_r$ weighted by a Green's function as (Kim 1989)

(5.4)\begin{equation} \left. \begin{array}{l@{}} \displaystyle {\hat p_r}(\boldsymbol{k},\omega ;y) = \int_{ - h}^h {G(y,y',k){{\hat f}_r} (\boldsymbol{k},\omega ;y')\,{{\rm d}y}'},\\ \displaystyle {\hat p_s}(\boldsymbol{k},\omega ;y) = \int_{ - h}^h {G(y,y',k){{\hat f}_s} (\boldsymbol{k},\omega ;y')\,{{\rm d}y}'}, \end{array}\right\} \end{equation}

where the Green's function $G(y,y',k)$ is given as

(5.5)\begin{equation} G(y,y',k) = \left\{ {\begin{array}{*{20}{@{}c}} {\dfrac{{\cosh (k(y' - h))\cosh (k(y + h))}}{{2k\sinh (kh)\cosh (kh)}},\quad y \le y'},\\ {\dfrac{{\cosh (k(y' + h))\cosh (k(y - h))}}{{2k\sinh (kh)\cosh (kh)}},\quad y > y'}, \end{array}}\right. \end{equation}

for $k\ne 0$, while for $k=0$ the Green's function is

(5.6)\begin{equation} G(y,y',k) = \left\{ {\begin{array}{*{20}{@{}c}} {\dfrac{1}{2}(y-y'),\quad y \le y'},\\ {\dfrac{1}{2}(y'-y),\quad y > y'}. \end{array}}\right. \end{equation}

In this paper, we focus on the wall pressure fluctuations, and as such the wall-normal coordinate is fixed to $y=\pm h$ without specific declarations.

From (5.1) and (5.3), it is known that the Fourier modes of wall pressure fluctuations can be also decomposed into rapid and slow components as

(5.7)\begin{equation} \hat p(\boldsymbol{k},\omega ) = {\hat p_r}(\boldsymbol{k},\omega ) + {\hat p_s}(\boldsymbol{k},\omega ). \end{equation}

Substituting (5.7) into (2.4) yields the following decomposition of the wavenumber–frequency spectrum of wall pressure fluctuations:

(5.8)\begin{align} {\phi _{pp}}(\boldsymbol{k},\omega ) &= {\phi _{rr}}(\boldsymbol{k},\omega ) + {\phi _{ss}}(\boldsymbol{k},\omega ) + 2{\phi _{rs}}(\boldsymbol{k},\omega ) \nonumber\\ &=\underbrace {\frac{{\overline {{{\hat p}_r}(\boldsymbol{k},\omega ) \hat p_r^*(\boldsymbol{k},\omega )} }}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z}{\rm \Delta} \omega }}}_{{{AS}} - {{Rapid}}} + \underbrace {\frac{{\overline {{{\hat p}_s}(\boldsymbol{k},\omega ) \hat p_s^*(\boldsymbol{k},\omega )} }}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z}{\rm \Delta} \omega }}}_{{{AS}} - {{Slow}}} + \underbrace {2\frac{{{{\rm Re}} \left( {\overline {{{\hat p}_r}(\boldsymbol{k},\omega ) \hat p_s^*(\boldsymbol{k},\omega )} } \right)}}{{{\rm \Delta} {k_x}{\rm \Delta} {k_z} {\rm \Delta} \omega }}}_{{{CS\text{-}RS}}}, \end{align}

where $\phi _{rr}(\boldsymbol {k},\omega )$, $\phi _{ss}(\boldsymbol {k},\omega )$ and $\phi _{rs}(\boldsymbol {k},\omega )$ represent AS-rapid, AS-slow and CS-RS, respectively, and ${\textrm {Re}} ( \cdot )$ denotes the real part of a complex number.

In the early research of wall pressure fluctuations, Kraichnan (1956) proposed a hypothesis that the rapid component of wall pressure fluctuations dominates over the slow component. This hypothesis is supported by the analytical studies of Hodgson (1962) and Chase (1980), and the experiments of Johansson, Her & Haritonidis (1987). Various predictive models of the spectrum of wall pressure fluctuations are proposed based on Kraichnan's hypothesis (see for example Kraichnan 1956; Panton & Linebarger 1974; Lee, Blake & Farabee 2005; Lysak 2006; Ahn, Graham & Rizzi 2010). In these models, the wavenumber–frequency spectrum of wall pressure fluctuations $\phi _{pp}(\boldsymbol {k},\omega )$ is approximated as the AS-rapid $\phi _{rr}(\boldsymbol {k},\omega )$. The DNS results of Kim (1989) and Chang III et al. (1999) show that the slow component of wall pressure fluctuations has the same order of magnitude as the rapid component. Therefore, it is more accurate to account for both AS-rapid and AS-slow to predict the spectrum of wall pressure fluctuations (see for example Chase 1980, 1987; Peltier & Hambric 2007; Slama et al. 2018; Grasso et al. 2019). In these models, the spectrum of the total wall pressure fluctuations is assumed to be the summation of AS-rapid and AS-slow, while CS-RS is neglected as a consequence of the joint-normal distribution assumption of the velocity fluctuations.

In this section, we use the DNS data to examine the influence of CS-RS on the spectrum of the total wall pressure fluctuations. To conduct quantitative analyses, there are two indicators evaluating the error induced by neglecting CS-RS. The first indicator is the ratio between CS-RS and the spectrum of the total wall pressure fluctuations, viz.

(5.9)\begin{equation} R = \frac{{2{\phi_{rs}}(\boldsymbol{k},\omega )}}{{{\phi _{pp}}(\boldsymbol{k},\omega )}}= \frac{\phi_{pp}(\boldsymbol{k},\omega )-(\phi_{rr}(\boldsymbol{k},\omega )+ \phi_{ss}(\boldsymbol{k},\omega ))}{\phi_{pp}(\boldsymbol{k},\omega )}\times 100\,\%. \end{equation}

When $\phi _{rr}(\boldsymbol {k},\omega )+\phi _{ss}(\boldsymbol {k},\omega )$ is used to approximate the ‘exact value’ of $\phi _{pp}(\boldsymbol {k},\omega )$ as is adopted in many models, the ratio $R$ also represents the relative error induced by neglecting $\phi _{rs}$. It can be proved using the Cauchy–Schwarz inequality that the value of $R$ ranges from $-\infty$ to $50\,\%$. The second indicator is the decibel-scaled error in $\phi _{pp}$ caused by neglecting $\phi _{rs}$, defined as

(5.10)\begin{equation} E = {10 \times {{\log }_{10}}\frac{{{\phi _{rr}}(\boldsymbol{k},\omega ) + {\phi _{ss}}(\boldsymbol{k},\omega )}}{{{\phi _{pp}}(\boldsymbol{k},\omega )}}} = {10 \times {{\log }_{10}}(1-R)}. \end{equation}

Since the spectrum of wall pressure fluctuations is conventionally presented in a decibel scale, we mainly use $E$ as the indicator in this paper. It is worth noting that the magnitudes of $R$ and $E$ are asymmetric for positive and negative values of $\phi _{rs}$. To be specific, if $\phi _{rs}\ge 0$, then $0\,\%\le R\le 50\,\%$ holds, and the corresponding decibel-scaled error $E$ is no smaller than $-3.0$ dB. However, if $\phi _{rs}< 0$, the relative error $R$ can reach $-\infty$ and the corresponding decibel-scaled error $E$ approaches $+\infty$. This suggests that if the value of $\phi _{rs}$ is negative and its magnitude is comparable to $\phi _{rr}+\phi _{ss}$, the wavenumber–frequency spectrum of wall pressure fluctuations can be significantly overestimated.

In the following content of this section, the characteristics of AS-rapid, AS-slow and CS-RS are discussed, and the errors in the spectra of the total wall pressure fluctuations caused by neglecting CS-RS are analysed. In §§ 5.2–5.4, the results of one-dimensional, two-dimensional and three-dimensional spectra at ${Re}_{\tau} =998$ are presented. The effects of Reynolds number are examined in § 5.5.

5.2. Decomposition of one-dimensional spectra

Figure 8 compares the magnitudes of one-dimensional AS-rapid, AS-slow and CS-RS. Note that $\phi _{rs}$ can be negative valued, such that its absolute value $|\phi _{rs}|$ is used to represent its magnitude in figure 8. To validate our results, the spectra of Abe et al. (2005) for AS-rapid and AS-slow with respect to the streamwise wavenumber $k_x$ are superposed in figure 8(a). It is seen that the present results agree with Abe et al. (2005).

Figure 8. One-dimensional AS-rapid (red solid lines), AS-slow (blue dashed lines) and the absolute value of CS-RS (green dash–dotted lines) with respect to the (a) streamwise wavenumber $k_x$, (b) spanwise wavenumber $k_z$ and (c) frequency $\omega$. The Reynolds number is $Re_\tau = 998$. The AS-rapid (red diamonds) and AS-slow (blue diamonds) with respect to the streamwise wavenumber $k_x$ of Abe et al. (2005) are superposed in panel (a) for comparison.

For the $k_x$- and $\omega$-spectra (see figures 8a and 8c, respectively), the magnitudes of $\phi _{rr}$ and $\phi _{ss}$ are comparable throughout the entire resolved range of $k_x$ and $\omega$, except that the magnitude of $\phi _{ss}$ is slightly larger than that of $\phi _{rr}$ at small $k_x$ or $\omega$. For the $k_z$-spectra, $\phi _{rr}$ is larger than $\phi _{ss}$ at small wavenumbers for $k_zh<10$, but becomes smaller than $\phi _{ss}$ at large wavenumbers for $k_zh>100$. These observations are consistent with the results of Kim (1989) and Chang III et al. (1999) at ${Re}_{\tau} =180$. The magnitudes of $\phi _{rr}$ and $\phi _{ss}$ are much larger than those of $|\phi _{rs}|$ at low wavenumbers ($k_xh<50$, $k_zh<50$) and low frequencies ($\omega h/u_\tau <500$), indicating that neglecting CS-RS causes little error in the one-dimensional spectra of the wall pressure fluctuation at these wavenumbers and frequencies. As the wavenumber or frequency increases, the magnitudes of $|\phi _{rs}|$, $\phi _{rr}$ and $\phi _{ss}$ become comparable at high wavenumbers ($k_xh>100$, $k_zh>200$) or high frequencies ($\omega h/u_\tau >1000$).

Figure 9 shows the decibel-scaled errors in the one-dimensional spectra of the total wall pressure fluctuations caused by neglecting CS-RS. At small wavenumbers or frequencies, $E$ is positive valued, and smaller than 1.0 dB. As the wavenumber or frequency increases, the value of $E$ decreases and crosses the dashed line denoting $E=0$ at ${k_x}h \approx 3.5$, ${k_z}h \approx 5.0$ and $\omega h/{u_\tau } \approx 80$. As the wavenumber or frequency continues to increase, the value of $E$ further decreases to its minimum and then increases slightly at very high wavenumbers or frequencies. The minimum values of $E$ for the $k_x$-, $k_z$- and $\omega$-spectra are approximately $-$2.1, $-$1.1 and $-$1.8 dB, respectively, suggesting that the assumption of neglecting CS-RS is acceptable for the one-dimensional spectra of wall pressure fluctuations.

Figure 9. Decibel-scaled errors in the one-dimensional (a) $k_x$-, (b) $k_z$- and (c) $\omega$-spectra of the wall pressure fluctuation caused by neglecting CS-RS.

5.3. Decomposition of the two-dimensional spectrum

In this subsection, we continue to investigate the decomposition of the two-dimensional spectrum of wall pressure fluctuations. To keep the paper concise, we follow Slama et al. (2018) to focus on the $k_x$–$\omega$ spectrum, since the energy-containing convective peak, which is important for the cabin noise generation of a high-speed subsonic civil aircraft (Graham 1997), can be identified from the $k_x$–$\omega$ spectrum.

The isopleths of two-dimensional AS-rapid and AS-slow in the $k_x$–$\omega$ plane are shown in figures 10(a) and 10(b), respectively. The difference between $\phi _{rr}$ and $\phi _{ss}$ mainly lies in the low-wavenumber region. As shown in figure 10(a), the isopleths of $\phi _{rr}$ contract to $({k_x},\omega ) = (0,0)$ as $k_x$ approaches zero. This property of $\phi _{rr}$ can be explained using the Helmholtz equation (5.3) of the Fourier modes of the rapid pressure fluctuations.

Figure 10. Contours of two-dimensional $k_x$–$\omega$ spectra of the (a) rapid and (b) slow components of the wall pressure fluctuation. Six equal-ratio isopleths from $1\times 10^{-5}$ to $1\times 10^{-10}$ are shown by the dashed lines. The convection lines $k_x=\omega /U_c$ are demarcated using the dash–dotted lines. The Reynolds number is $Re_\tau = 998$.

The source term of the rapid pressure fluctuations in the wavenumber–frequency space, i.e. ${\hat f}_r(\boldsymbol {k},\omega ;y')$ in (5.4), can be written as

(5.11)\begin{align} {\hat f_r}(\boldsymbol{k},\omega ;y) &= \frac{1}{{{{(2{\rm \pi} )}^3}}} \int {{\rm d}x} \int {{\rm d} z} \int {{\rm d} t } \cdot \left( { - 2\frac{{{\rm d} U}}{{{\rm d}y}} \frac{{\partial v}}{{\partial x}}} \right)\exp [ - {\rm i}({k_x}x + {k_z}z - \omega t)] \nonumber\\ &={-} \frac{{2{\rm{i}}{k_x}}}{{{{(2{\rm \pi} )}^3}}}\frac{{{\rm d} U(y)}}{{{\rm d}y}} \hat v(\boldsymbol{k},\omega ;y), \end{align}

from which it is understood that ${\hat f}_r(k_x=0,k_z,\omega ;y)=0$. Furthermore, (5.5) and (5.6) show that the Green's function approaches a non-zero finite value as $k_x\to 0$, and, therefore, ${\hat p_r}(k_x=0,k_z,\omega ;y)=0$ holds. Integrating $\phi _{rr}(k_x,k_z,\omega )$ over the spanwise wavenumber $k_z$ yields the same constraint for the two-dimensional spectrum $\phi _{rr}(k_x,\omega )$. This constraint also leads to the contracting behaviour of the isopleths of $\phi _{pp}$ around $k_x=0$ as shown in figure 3. In contrast, the source term of the slow pressure fluctuations does not have such a constraint at $k_x=0$. Consequently, the isopleths of AS-slow do not show a contracting feature around $k_x=0$ (figure 10b).

Both $\phi _{rr}$ and $\phi _{ss}$ show a convective property. Specifically, the large spectral values are concentrated around the convection lines demarcated by the dash–dotted lines. The slopes of the convection lines are identical to the bulk convection velocity, which can be determined using (3.1). The values of the bulk convection velocity for $\phi _{rr}$ and $\phi _{ss}$ are $11.5{u_\tau }$ and $11.7{u_\tau }$, respectively, close to the bulk convection velocity of the total wall pressure fluctuations, i.e. $11.6{u_\tau }$ as shown in figure 3(a). Figure 11 further compares the wavenumber-dependent convection velocities of the rapid, slow and total wall pressure fluctuations. Here, the wavenumber-dependent convection velocity of an arbitrary variable is defined using its wavenumber–frequency spectrum $\phi (k_x,\omega )$ as (del Álamo & Jiménez 2009)

(5.12)\begin{equation} {U_{c}}({k_x}) = \frac{{\int {\omega \phi ({k_x},\omega )\,{\rm d}\omega } }}{{{k_x} \int {\phi ({k_x},\omega )\,{\rm d}\omega } }}. \end{equation}

From figure 11, it is seen that the values of ${U_{c}}({k_x})$ for the rapid, slow and total wall pressure fluctuations all decrease monotonically as $k_x$ increases. At low wavenumbers for $k_xh<10$, the convection velocity of the rapid wall pressure fluctuations is larger than that of the slow wall pressure fluctuations. For $k_xh>10$, the convection velocities of the rapid, slow and total wall pressure fluctuations are close to each other. They all approach $10.0u_\tau$ as $k_x$ increases. This value is close to the convection velocity of the total wall pressure fluctuations at ${{Re}}_{\tau }=180$ (Choi & Moin 1990). These results indicate that the convective properties of the rapid and slow pressure are similar, and the same convection velocity can be used to model both AS-rapid and AS-slow (Chase 1980, 1987).

Figure 11. Wavenumber-dependent convection velocities of the rapid, slow and total wall pressure fluctuations. The Reynolds number is $Re_\tau = 998$.

Figure 12 shows the contours of CS-RS in the $k_x$–$\omega$ plane with the positive and negative values coloured by red and blue, respectively. It is seen that CS-RS is positive in most regions around the convection line (denoted by the dash–dotted line), except for a small region below the convection line at relatively low $k_x$. Besides, since CS-RS also satisfies the constraint $\phi _{rs}(k_x,\omega )\to 0$ as $k_x$ approaches zero, the isopleths show similar contracting behaviour as $\phi _{rr}(k_x,\omega )$ (see figure 10a) at low streamwise wavenumbers.

Figure 12. Contours of two-dimensional CS-RS in the $k_x$–$\omega$ plane. The positive and negative values are coloured by red and blue, respectively. The convection line $k_x=\omega /U_c$ is demarcated using the dash–dotted line. The Reynolds number is $Re_\tau = 998$.

Figure 13 shows the contours of the decibel-scaled error $E$ in the $k_x$–$\omega$ spectrum of wall pressure fluctuations caused by neglecting CS-RS. The positively and negatively valued regions are coloured by red and blue, respectively. It is seen that there are three local peaks, two in the blue region with negative value of $E$ (marked by the white cross symbols), and one in the red region with positive value of $E$ (marked by the black cross symbol). The details of these peaks, including their locations and values, are given in the figure. Specifically, there are two negative peaks, with one located in the subconvective region and the other in the viscous region. The values of $E$ for these two peaks are $-$2.0 and $-$2.5 dB, respectively. The positive peak is located below the convection line, and its decibel-scaled value is 1.4 dB.

Figure 13. Contours of the decibel-scaled error $E$ in the $k_x$–$\omega$ spectrum of wall pressure fluctuations caused by neglecting CS-RS. The local peaks in the regions with negative and positive values of $E$ are marked using the white and black cross symbols, respectively. The Reynolds number is $Re_\tau = 998$.

In summary, neglecting CS-RS leads to a maximum decibel-scaled error of approximately $-$2.5 dB at viscous scales for the $k_x$–$\omega$ spectrum of wall pressure fluctuations. This is still an acceptable error magnitude, though it is slightly larger than that in the one-dimensional spectra. In § 5.4, we continue to show that for the three-dimensional spectrum of wall pressure fluctuations, a much larger decibel-scaled error of approximately 4.7 dB in the subconvective region is induced by neglecting CS-RS.

5.4. Decomposition of the three-dimensional spectrum

Figure 14 compares the variations of $\phi _{rr}$, $\phi _{ss}$ and $|\phi _{rs}|$ with respect to $k_x$ at $k_z=0$ and two given frequencies $\omega h/{u_\tau } = 245$ and $\omega h/{u_\tau } = 716$. The corresponding convective wavenumbers demarcated by the vertical dashed lines are $k_xh=15$ and $k_xh=48$, respectively. From these convective wavenumbers and frequencies, it can be calculated that the convection velocities at these two frequencies are $16.3u_{\tau }$ and $14.9u_{\tau }$, respectively. These values are larger than the convection velocity shown in figure 11. Such a difference is attributed to the fact that figure 14 shows the three-dimensional spectrum at a specific spanwise wavenumber $k_z=0$, while in figure 11, the convection velocity of the two-dimensional spectrum averaged over all spanwise wavenumbers is depicted. The above comparison indicates that the convection velocity also depends on the spanwise wavenumber. This is consistent with the results of del Álamo & Jiménez (2009).

Figure 14. Absolute values of AS-rapid $\phi _{rr}$, AS-slow $\phi _{ss}$ and CS-RS $|\phi _{rs}|$ for the three-dimensional wavenumber–frequency spectra of wall pressure fluctuations for $k_z=0$ and two given frequencies (a) $\omega h/{u_\tau } = 245$ and (b) $\omega h/{u_\tau } = 716$. The convective wavenumbers are demarcated using vertical dashed lines. The Reynolds number is $Re_\tau = 998$.

The spectra at the two frequencies have some common features. First, in the subconvective region (left-hand side of the vertical dashed lines), the magnitudes of $|\phi _{rs}|$ and $\phi _{rr}$ are comparable, while that of $\phi _{ss}$ is large. Second, as $k_x$ increases to the convective wavenumber, the magnitudes of $\phi _{rr}$ and $\phi _{ss}$ become close to each other gradually, while $|\phi _{rs}|$ becomes one order of magnitude smaller than $\phi _{rr}$ and $\phi _{ss}$ (shown by the horizontal dotted lines in figure 14). Finally, the magnitudes of $|\phi _{rs}|$, $\phi _{rr}$ and $\phi _{ss}$ become close to each other for $k_xh>200$.

Next, we focus on the error in the three-dimensional spectrum of wall pressure fluctuations caused by neglecting CS-RS. By examining the decibel-scaled error in the $k_x$–$k_z$ plane at various frequencies (not shown for brevity), we find that for an arbitrarily given combination of $(k_x, \omega )$, the peak of $E$ always occurs at $k_z = 0$. Therefore, we focus on $k_z = 0$ in the following error analyses. Figure 15 shows the $k_x$-variation of the decibel-scaled error $E$ at $k_z=0$ and two frequencies $\omega h/{u_\tau } = 245$ and $\omega h/{u_\tau } = 716$. Since the raw data (denoted by the grey lines in figure 15) fluctuate violently, we follow Baars, Hutchins & Marusic (2016) to adopt a moving average filter to show the qualitative trend. The moving average filter is expressed as

(5.13)\begin{equation} {E_{{{filt}}}}({k_x}) = \sum_{i ={-} l}^l {\frac{1}{{2l + 1}}E({k_x} + i{\rm \Delta} {k_x})}, \end{equation}

where the filter width is chosen to be $l=2$. The filtered results are denoted by the black lines in figure 15. For both frequencies, the maximum values of $E$ (denoted by red circles in figure 15) occur in the subconvective region. At the lower frequency $\omega h/u_\tau =245$, the maximum values of unfiltered and filtered error reach 5.1 and 4.1 dB, respectively. At the higher frequency, these two values decrease to 2.9 and 2.5 dB, respectively. The results shown in figure 15 indicate a significant overprediction of the spectral magnitude in the subconvective region.

Figure 15. Unfiltered (grey lines) and filtered (black lines) error $E$ in the three-dimensional wavenumber–frequency spectrum caused by neglecting CS-RS for $k_z=0$ and two given frequencies (a) $\omega h/{u_\tau } = 245$ and (b) $\omega h/{u_\tau } = 716$. The convective wavenumbers are demarcated using vertical dashed lines. The Reynolds number is $Re_\tau = 998$.

While figure 15 shows the error at specific frequencies, it is also useful to find the maximum error over all frequencies. For this purpose, we define the frequency-dependent maximum error ${E_{max}}(\omega )$ as

(5.14)\begin{equation} {E_{max}}(\omega ) = \max_{{k_x}} E({k_x},{k_z} = 0,\omega). \end{equation}

Figure 16 shows the variation of $E_{max}$ with respect to the dimensionless frequency $\omega h / u_\tau$. The raw data and filtered data are denoted by the grey and red lines, respectively. The peak of $E_{\max }$ occurs at a low frequency, of which the value is 4.7 and 5.2 dB with and without the application of the filter, respectively. Such a decibel-scaled error (4.7 dB) corresponds to a large relative error of approximately 195 % caused by neglecting CS-RS in the model of the three-dimensional spectrum of wall pressure fluctuations.

Figure 16. Unfiltered (grey line) and filtered (red line) frequency-dependent maximum error $E_{max}$ in the three-dimensional wavenumber–frequency spectrum of wall pressure fluctuations caused by neglecting CS-RS. The Reynolds number is $Re_\tau = 998$.

It should be noted here that in practical applications, the total wall pressure fluctuations are a weighted integration of their spectrum at all wavenumbers and frequencies. Therefore, the error in the subconvective region can be attenuated. This is supported by the fact that the errors in one- and two-dimensional spectra are smaller than those in the three-dimensional spectrum. However, the findings of this section cast a doubt on the conventional assumption that CS-RS is negligible compared with AS-rapid and AS-slow in some specific applications. In particular, neglecting CS-RS induces significant errors in the subconvective region at low frequencies. As pointed out by Graham (1997), the properties of the wavenumber–frequency spectrum model in the subconvective region are crucial for the prediction of noise generation in low-Mach-number flows over stiff structures. The omission of CS-RS can be, therefore, inaccurate in corresponding applications, such as automobiles and submarine vehicles, and a modification is expected.

5.5. Reynolds number effects

The above analyses of the error in the spectrum of wall pressure fluctuations caused by neglecting CS-RS are conducted at ${{Re}}=998$. In this subsection, we further examine the effect of Reynolds number. Because the errors in the one- and two-dimensional spectra are acceptable, while those in the three-dimensional spectrum are significantly larger, we focus on the three-dimensional spectrum in this subsection to keep the paper concise.

Figure 17 compares the variations of the filtered value of $E_{max}$ (see (5.14) for definition) with respect to the viscous-scaled frequency for various Reynolds numbers. It is observed that the distributions of $E_{max}$ are close to each other for $330\lesssim {Re}_{\tau} \lesssim 1000$ under the viscous scaling. Specifically, the peak occurs at $\omega ^+\approx 0.25$ and the peak value is approximately 4.7 dB. For the lowest Reynolds number ${Re}_{\tau} =180$, the peak is located at a slightly lower frequency $\omega ^+\approx 1.5$ and the peak value is approximately 6.0 dB. The difference might be induced by the low-Reynolds-number effect. This observation indicates that the maximum error in the wavenumber–frequency spectrum of wall pressure fluctuations induced by neglecting CS-RS is correlated to the property of the velocity field in the near-wall region.

Figure 17. Variation of filtered $E_{max}$ with respect to the viscous-scaled frequency $\omega ^+$ for different Reynolds numbers.

6. Conclusions

In this paper, we conduct DNS of turbulent channel flows at four Reynolds numbers (${Re}_{\tau} =179,333,551,998$) to study the wavenumber–frequency spectrum of wall pressure fluctuations. The characteristics of the wavenumber–frequency spectrum of the total wall pressure fluctuations, along with AS-rapid, AS-slow and CS-RS, are analysed with particular focus on the assumption that CS-RS is negligibly small compared with AS-rapid and AS-slow, which is commonly used in various models of the wavenumber–frequency spectrum of wall pressure fluctuations. We also conduct an investigation of the time decorrelation of wall pressure fluctuations. The main findings of this paper are summarized as follows.

For the two-dimensional and three-dimensional spectra of the total wall pressure fluctuations, the isopleths gradually contract to the origin as the streamwise wavenumber $k_x$ approaches zero. This contracting behaviour is determined by the mathematical constraint of AS-rapid $\lim _{{k_x} \to 0} {\phi _{rr}}({k_x},k_z,\omega ) =0$, which is proved using the solution of the Helmholtz equation based on the Green's function.

In the investigation of the time decorrelation mechanisms, it is discovered that the frequency distributions of the wavenumber–frequency spectrum of wall pressure fluctuations at energy-containing scales follow a similar Gaussian form as those of streamwise velocity fluctuations. The sweeping velocities are close to the r.m.s. velocity fluctuations at the centre of the buffer layer. This indicates that the time decorrelation of wall pressure fluctuation is also dominated by the random sweeping, and the energy-containing part of the wavenumber–frequency spectrum of wall pressure fluctuations can be well predicted using a random sweeping model.

In the analyses of the model error caused by neglecting CS-RS, it is found that the assumption that CS-RS can be neglected in comparison with AS-rapid and AS-slow is acceptable for one- and two-dimensional spectra. However, for the three-dimensional spectrum, neglecting CS-RS leads to a significant over-prediction of the spectrum in the subconvective region. The maximal decibel-scaled error is approximately 4.7 dB for $330\lesssim {Re}_{\tau} \lesssim 1000$. Furthermore, the frequency corresponding to the maximum error is scaled by the wall units, indicating that the error is correlated to the velocity sources in the near-wall region. These results show that in the predictive models of the wavenumber–frequency spectrum of wall pressure fluctuations, more efforts are needed to account for CS-RS in the subconvective region.

As a final remark in this paper, we note that due to the influence of the artificial acoustic, the wavenumber–frequency spectrum of wall pressure fluctuations at small wavenumbers is not analysed thoroughly in this paper. However, the flow-induced low-wavenumber wall pressure fluctuation plays an important role in structure vibration (Graham 1997). In future studies, it is desired to conduct simulations using sufficiently large computational domain to examine the corresponding theories (Kraichnan 1956; Phillips 1956) and physical models (e.g. Chase 1980, 1987) at small wavenumbers.