Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T21:41:08.724Z Has data issue: false hasContentIssue false
  • English
  • Français

On the thin-film asymptotics of surface tension driven microfluidics

Published online by Cambridge University Press:  19 August 2020

S. N. Calver Open the ORCID record for S. N. Calver [Opens in a new window] ,
E. A. Gaffney ,
E. J. Walsh ,
W. M. Durham  and
J. M. Oliver
S. N. Calver*
Affiliation:
Wolfson Centre for Mathematical Biology, Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK
E. A. Gaffney
Affiliation:
Wolfson Centre for Mathematical Biology, Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK
E. J. Walsh
Affiliation:
Department of Engineering Science, Osney Thermo-Fluids Laboratory, University of Oxford, Osney Mead, OxfordOX2 0ES, UK
W. M. Durham
Affiliation:
Department of Zoology, University of Oxford, South Parks Road, OxfordOX1 3PS, UK Department of Physics and Astronomy, University of Sheffield, Hounsfield Road, SheffieldS3 7RH, UK
J. M. Oliver
Affiliation:
Mathematical Institute, University of Oxford, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Road, OxfordOX2 6GG, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

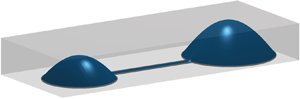
Recent technological advances have led to a novel class of microfluidic devices which can be rapidly fabricated by printing a fluid onto a solid substrate with flows generated passively via surface tension. The nonlinear dependence between flow and the heights of the conduits, however, prevent straightforward calculation of the resulting dynamics. In this paper we use matched asymptotic expansions to predict how flow through these devices can be tuned by changing their geometry. We begin with the simple ‘dumbbell’ configuration in which two fluid drops with different sizes are connected by a long, thin and narrow conduit. We calculate the time scale required for one drop to drain into the other and how this depends both on the geometry of the pinned contact line and volume of fluid deposited into the drops. Our model therefore provides the mechanistic basis to design conduits with a particular fluid flux and/or shear stress, which are often key experimental constraints. Our asymptotic predictions are shown to be in excellent agreement with numerical simulations even for moderate aspect ratios (the ratio of conduit width to length). Next, we show how our results for the simple dumbbell configuration can be extended to predict the flow through networks of conduits with multiple drops and nodes, and hence may assist in their design and implementation. This new mathematical framework has the potential to increase the use of surface tension driven microfluidics across a wide range of disciplines as it allows alternate designs to be rapidly assessed.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 901 , 25 October 2020 , A6
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Al Mukahal, F. H. H., Duffy, B. R. & Wilson, S. K. 2017 Advection and Taylor–Aris dispersion in rivulet flow. Proc. R. Soc. Lond. A 473 (2207), 20170607.10.1098/rspa.2017.0524CrossRefGoogle ScholarPubMed
Becker, H. & Gärtner, C. 2008 Polymer microfabrication technologies for microfluidic systems. Anal. Bioanal. Chem. 390 (1), 89–111.10.1007/s00216-007-1692-2CrossRefGoogle ScholarPubMed
Bélanger, M. C. & Marois, Y. 2001 Hemocompatibility, biocompatibility, inflammatory and in vivo studies of primary reference materials low-density polyethylene and polydimethylsiloxane: a review. J. Biomed. Mater. Res. 58 (5), 467–77.10.1002/jbm.1043CrossRefGoogle ScholarPubMed
Carvajal, Daniel, Laprade, Evan J., Henderson, Kevin J. & Shull, Kenneth R. 2011 Mechanics of pendant drops and axisymmetric membranes. Soft Matter 7 (22), 10508–10519.10.1039/c1sm05703kCrossRefGoogle Scholar
Chesters, A. K. 1977 An analytical solution for the profile and volume of a small drop or bubble symmetrical about a vertical axis. J. Fluid Mech. 81 (4), 609–624.10.1017/S0022112077002250CrossRefGoogle Scholar
COMSOL Multiphysics®v.5.4 2018 COMSOL Multiphysics Reference Manual. Stockholm.Google Scholar
Darhuber, A. A., Chen, J. Z., Davis, J. M. & Troian, S. M. 2004 A study of mixing in thermocapillary flows on micropatterned surfaces. Phil. Trans. R. Soc. Lond. A 362 (1818), 1037–1058.10.1098/rsta.2003.1361CrossRefGoogle ScholarPubMed
Driscoll, T. A. 1996 Algorithm 756; a MATLAB toolbox for Schwarz–Christoffel mapping. ACM Trans. Math. Softw. 22 (2), 168–186.10.1145/229473.229475CrossRefGoogle Scholar
Driscoll, T. A. & Trefethen, L. N. 2002 Schwarz–Christoffel Mapping. Cambridge University Press.10.1017/CBO9780511546808CrossRefGoogle Scholar
Halldorsson, S., Lucumi, E., Gómez-Sjöberg, R. & Fleming, R. M. T. 2015 Advantages and challenges of microfluidic cell culture in polydimethylsiloxane devices. Biosens. Bioelectr. 63, 218–231.10.1016/j.bios.2014.07.029CrossRefGoogle ScholarPubMed
Holmes, D. & Gawad, S. 2010 The application of microfluidics in biology. Meth. Mol. Biol. 583, 55–88.10.1007/978-1-60327-106-6_2CrossRefGoogle ScholarPubMed
Lee, H., Lee, S. G. & Doyle, P. S. 2015 Photopatterned oil-reservoir micromodels with tailored wetting properties. Lab on a Chip 15, 3047–3055.10.1039/C5LC00277JCrossRefGoogle ScholarPubMed
Lee, J. N., Park, C. & Whitesides, G. M. 2003 Solvent compatibility of poly(dimethylsiloxane)-based microfluidic devices. Anal. Chem. 75 (23), 6544–6554.10.1021/ac0346712CrossRefGoogle ScholarPubMed
Lighthill, J. 1975 Mathematical Biofluiddynamics. SIAM.10.1137/1.9781611970517CrossRefGoogle Scholar
Marušić-Paloka, E. 2001 Fluid flow through a network of thin pipes. C. R. Acad. Sci. 329 (2), 103–108.Google Scholar
McDonald, J. C., Duffy, D. C., Anderson, J. R., Chiu, D. T., Wu, H., Schueller, O. J. A. & Whitesides, G. M. 2000 Fabrication of microfluidic systems in poly(dimethylsiloxane). Electrophoresis 21 (1), 27–40.10.1002/(SICI)1522-2683(20000101)21:1<27::AID-ELPS27>3.0.CO;2-C3.0.CO;2-C>CrossRefGoogle Scholar
Mehling, M. & Tay, S. 2014 Microfluidic cell culture. Curr. Opin. Biotechnol. 25, 95–102.10.1016/j.copbio.2013.10.005CrossRefGoogle ScholarPubMed
Nge, P. N., Rogers, C. I. & Woolley, A. T. 2013 Advances in microfluidic materials, functions, integration, and applications. Chem. Rev. 113 (4), 2550–2583.10.1021/cr300337xCrossRefGoogle ScholarPubMed
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69 (3), 931–980.10.1103/RevModPhys.69.931CrossRefGoogle Scholar
Paguirigan, A. L. & Beebe, D. J. 2008 Microfluidics meet cell biology: bridging the gap by validation and application of microscale techniques for cell biological assays. BioEssays 30 (9), 811–821.10.1002/bies.20804CrossRefGoogle ScholarPubMed
Paguirigan, A. L. & Beebe, D. J. 2009 From the cellular perspective: exploring differences in the cellular baseline in macroscale and microfluidic cultures. Integr. Biol. 1 (2), 182–195.CrossRefGoogle ScholarPubMed
Paterson, C., Wilson, S. K. & Duffy, B. R. 2013 Pinning, de-pinning and re-pinning of a slowly varying rivulet. Eur. J. Mech. B/Fluids 41, 94–108.10.1016/j.euromechflu.2013.02.006CrossRefGoogle Scholar
Ren, K., Chen, Y. & Wu, H. 2014 New materials for microfluidics in biology. Curr. Opin. Biotechnol. 25, 78–85.10.1016/j.copbio.2013.09.004CrossRefGoogle ScholarPubMed
Sackmann, E. K., Fulton, A. L. & Beebe, D. J. 2014 The present and future role of microfluidics in biomedical research. Nature 507 (7491), 181–189.10.1038/nature13118CrossRefGoogle ScholarPubMed
Stathopoulos, N. A. & Hellums, J. D. 1985 Shear stress effects on human embryonic kidney cellsin vitro. Biotechnol. Bioengng 27 (7), 1021–1026.10.1002/bit.260270713CrossRefGoogle Scholar
Stone, H. A., Stroock, A. D. & Ajdari, A. 2004 Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 36 (1), 347–382.CrossRefGoogle Scholar
Thomson, W. 1886 Capillary attraction. Nature 34, 290–294.10.1038/034290c0CrossRefGoogle Scholar
Toepke, M. W. & Beebe, D. J. 2006 PDMS absorption of small molecules and consequences in microfluidic applications. Lab on a Chip 6 (12), 1484–1486.CrossRefGoogle ScholarPubMed
Towell, G. D. & Rothfeld, L. B. 1966 Hydrodynamics of rivulet flow. AIChE J. 12 (5), 972–980.10.1002/aic.690120524CrossRefGoogle Scholar
Van Lengerich, H. B., Vogel, M. J. & Steen, P. H. 2010 Coarsening of capillary drops coupled by conduit networks. Phys. Rev. E 82 (6).10.1103/PhysRevE.82.066312CrossRefGoogle ScholarPubMed
Walsh, E. J., Feuerborn, A., Wheeler, J. H. R., Tan, A. N., Durham, W. M., Foster, K. R. & Cook, P. R. 2017 Microfluidics with fluid walls. Nat. Commun. 8 (1), 816.CrossRefGoogle ScholarPubMed
Whitesides, G. M. 2006 The origins and the future of microfluidics. Nature 442 (7101), 368–373.CrossRefGoogle ScholarPubMed
Xia, Y. & Whitesides, G. M. 1998 Soft lithography. Annu. Rev. Mater. Sci. 28 (12), 153–184.10.1146/annurev.matsci.28.1.153CrossRefGoogle Scholar