Published online by Cambridge University Press: 15 January 2018
We consider fully developed turbulence in straight ducts of non-circular cross-sectional shape, for instance a square. A global friction velocity 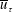 $\overline{u}_{\unicode[STIX]{x1D70F}}$ is defined from the streamwise pressure gradient
$\overline{u}_{\unicode[STIX]{x1D70F}}$ is defined from the streamwise pressure gradient 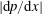 $|\text{d}p/\text{d}x|$ and a single characteristic length
$|\text{d}p/\text{d}x|$ and a single characteristic length 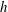 $h$, half the hydraulic diameter (shapes with disparate length scales, due to high aspect ratio, are excluded). We reason that as the Reynolds number
$h$, half the hydraulic diameter (shapes with disparate length scales, due to high aspect ratio, are excluded). We reason that as the Reynolds number 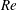 $Re$ reaches high values, outside the viscous region the streamwise velocity differences and the secondary motion scale with
$Re$ reaches high values, outside the viscous region the streamwise velocity differences and the secondary motion scale with 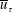 $\overline{u}_{\unicode[STIX]{x1D70F}}$ and the Reynolds stresses with
$\overline{u}_{\unicode[STIX]{x1D70F}}$ and the Reynolds stresses with 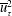 $\overline{u}_{\unicode[STIX]{x1D70F}}^{2}$. This extends the classical defect-law argument, associated with Townsend and many others, and is successful in channel and pipe flows. We then posit matched asymptotic expansions with overlap of the law of the wall and the behaviour we assumed in the core region. The wall may be smooth, or have a Nikuradse roughness
$\overline{u}_{\unicode[STIX]{x1D70F}}^{2}$. This extends the classical defect-law argument, associated with Townsend and many others, and is successful in channel and pipe flows. We then posit matched asymptotic expansions with overlap of the law of the wall and the behaviour we assumed in the core region. The wall may be smooth, or have a Nikuradse roughness 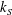 $k_{S}$ (such that it is fully rough, with
$k_{S}$ (such that it is fully rough, with 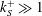 $k_{S}^{+}\gg 1$). The consequences include the familiar logarithmic behaviour of the velocity profile, but also the surprising prediction that the skin friction tends to uniformity all around the duct, except near possible corners, asymptotically as
$k_{S}^{+}\gg 1$). The consequences include the familiar logarithmic behaviour of the velocity profile, but also the surprising prediction that the skin friction tends to uniformity all around the duct, except near possible corners, asymptotically as 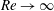 $Re\rightarrow \infty$ or
$Re\rightarrow \infty$ or 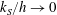 $k_{S}/h\rightarrow 0$. This is confirmed by numerical solutions for a square and two ellipses, using a conventional turbulence model, albeit the trend with Reynolds number is slow. The magnitude of the secondary motion also scales as expected, and the skin-friction coefficient follows the logarithm of the appropriate Reynolds number. This is a validation of the mathematical reasoning, but is by no means independent physical evidence, because the turbulence models embody the same assumptions as the theory. The uniformity of the skin friction appears to be a new and falsifiable deduction from turbulence theory, and a candidate for high-Reynolds-number experiments.
$k_{S}/h\rightarrow 0$. This is confirmed by numerical solutions for a square and two ellipses, using a conventional turbulence model, albeit the trend with Reynolds number is slow. The magnitude of the secondary motion also scales as expected, and the skin-friction coefficient follows the logarithm of the appropriate Reynolds number. This is a validation of the mathematical reasoning, but is by no means independent physical evidence, because the turbulence models embody the same assumptions as the theory. The uniformity of the skin friction appears to be a new and falsifiable deduction from turbulence theory, and a candidate for high-Reynolds-number experiments.