1. Introduction
As summarized in reviews (Gad-el Hak Reference Gad-el Hak1986a; Carpenter, Davies & Lucey Reference Carpenter, Davies and Lucey2000), the interactions between compliant surfaces and boundary layers have been investigated extensively since the bio-inspired attempts to reduce skin friction by Kramer (Reference Kramer1960). Linear theoretical models predicting the response of viscoelastic coatings to uniform harmonic excitation by pressure and shear stress based on solutions to the Helmholtz equation have been discussed in Chase (Reference Chase1991) and Benschop et al. (Reference Benschop, Greidanus, Delfos, Westerweel and Breugem2019). They predict that the wavelength of peak wall response is three times the wall thickness, and that the pressure is the dominant contributor to the deformation. While early numerical simulations model the wall using springs and dampers (e.g. Kim & Choi Reference Kim and Choi2014), recent direct numerical simulations (DNS) already compute the flow in the boundary layer and within the compliant wall (Rosti & Brandt Reference Rosti and Brandt2017; Esteghamatian, Katz & Zaki Reference Esteghamatian, Katz and Zaki2022). Experimental velocity profiles in the inner part of the boundary layers and the wall deformation are available in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017), Wang, Koley & Katz (Reference Wang, Koley and Katz2020) and Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022). While trends vary, these DNS and experiments show a decrease in the velocity in the buffer and viscous sublayers that increases in severity with the deformation amplitude relative to the wall unit, ![]() $\delta _\nu =\nu /u_\tau$, where
$\delta _\nu =\nu /u_\tau$, where ![]() $\nu$ is the kinematic viscosity and
$\nu$ is the kinematic viscosity and ![]() $u_\tau =(\tau _w/\rho)^{(1/2)}$, with
$u_\tau =(\tau _w/\rho)^{(1/2)}$, with ![]() $\tau _w$ and
$\tau _w$ and ![]() $\rho$ being the wall shear stress and fluid density, respectively. Wang et al. (Reference Wang, Koley and Katz2020) and Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022) observe deviations in the inner- layer profiles even for deformation amplitudes,
$\rho$ being the wall shear stress and fluid density, respectively. Wang et al. (Reference Wang, Koley and Katz2020) and Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022) observe deviations in the inner- layer profiles even for deformation amplitudes, ![]() $d$, much smaller than
$d$, much smaller than ![]() $\delta _\nu (d^+=d/\delta _\nu \ll 1)$. The extent of influence on the magnitude and slope of the log layer profiles differs among these studies.
$\delta _\nu (d^+=d/\delta _\nu \ll 1)$. The extent of influence on the magnitude and slope of the log layer profiles differs among these studies.
The present analysis of recently obtained experimental data highlights the importance of a ‘critical layer’ introduced by Miles (Reference Miles1957) for characterizing wind–wave interactions in oceanography. At the critical height, ![]() $y=y_c$, the mean streamwise velocity,
$y=y_c$, the mean streamwise velocity, ![]() $U(y)$, is equal to the surface wave speed,
$U(y)$, is equal to the surface wave speed, ![]() $U_{sw}$. Lighthill (Reference Lighthill1962) demonstrates that the energy transfer from the wind to the wave is concentrated at the critical layer, but since it is separated from the wave, the interaction occurs at all
$U_{sw}$. Lighthill (Reference Lighthill1962) demonstrates that the energy transfer from the wind to the wave is concentrated at the critical layer, but since it is separated from the wave, the interaction occurs at all ![]() $y< y_c$. Numerous studies, e.g. Young & Wolfe (Reference Young and Wolfe2014) and Carpenter, Guha & Heifetz (Reference Carpenter, Guha and Heifetz2017), have since attempted to model this energy transfer, and the latter has been validated recently by Carpenter, Buckley & Veron (Reference Carpenter, Buckley and Veron2022) using experimental data. In this paper, we demonstrate the important role that the critical layer plays in interactions between a compliant wall and a turbulent boundary layer.
$y< y_c$. Numerous studies, e.g. Young & Wolfe (Reference Young and Wolfe2014) and Carpenter, Guha & Heifetz (Reference Carpenter, Guha and Heifetz2017), have since attempted to model this energy transfer, and the latter has been validated recently by Carpenter, Buckley & Veron (Reference Carpenter, Buckley and Veron2022) using experimental data. In this paper, we demonstrate the important role that the critical layer plays in interactions between a compliant wall and a turbulent boundary layer.
The present experiments involve simultaneous measurements of the time-resolved three-dimensional (3-D) velocity and pressure fields as well as the two-dimensional (2-D) distribution of surface deformation. Data are obtained at three friction Reynolds numbers (![]() $Re_\tau =u_\tau \delta /\nu$, where
$Re_\tau =u_\tau \delta /\nu$, where ![]() $\delta$ is the boundary-layer thickness), hence there are different deformation magnitudes relative to the boundary-layer length scales. Combining data from several references, we show that trends of the deformation r.m.s. scaled by the compliant wall thickness collapse and are nearly linear when plotted vs pressure fluctuations scaled by the shear modulus. The pressure–deformation correlation peaks at or slightly above
$\delta$ is the boundary-layer thickness), hence there are different deformation magnitudes relative to the boundary-layer length scales. Combining data from several references, we show that trends of the deformation r.m.s. scaled by the compliant wall thickness collapse and are nearly linear when plotted vs pressure fluctuations scaled by the shear modulus. The pressure–deformation correlation peaks at or slightly above ![]() $y_c$, which is located in the log layer. At lower elevations, wavenumber–frequency spectra of pressure and vertical velocity fluctuations indicate that the turbulence is phase locked and travels with the deformation, even for
$y_c$, which is located in the log layer. At lower elevations, wavenumber–frequency spectra of pressure and vertical velocity fluctuations indicate that the turbulence is phase locked and travels with the deformation, even for ![]() $d^+\ll 1$. In contrast, at
$d^+\ll 1$. In contrast, at ![]() $y>y_c$, the turbulence is advected at the local mean streamwise velocity, and its correlation with the deformation decays rapidly. These trends differ fundamentally from those of smooth wall boundary layers. The outline of the paper is as follows: § 2 presents the experimental set-up and data processing procedures, results are discussed in § 3 and conclusions are summarized in § 4.
$y>y_c$, the turbulence is advected at the local mean streamwise velocity, and its correlation with the deformation decays rapidly. These trends differ fundamentally from those of smooth wall boundary layers. The outline of the paper is as follows: § 2 presents the experimental set-up and data processing procedures, results are discussed in § 3 and conclusions are summarized in § 4.
2. Experimental set-up and measurement procedures
The present measurements are performed in a recently constructed refractive-index- matched water tunnel, which uses the same inlet diffuser, settling chamber, test section and diffuser as those described in Wang et al. (Reference Wang, Koley and Katz2020). However, additional screens are added to the settling chamber to reduce the free-stream turbulence. Recent Particle Image Velocimetry (PIV) measurements show that the r.m.s. of free-stream velocity fluctuations is less than 0.7 %. The fluid is a 62 % by weight aqueous NaI solution that has the same refractive index (1.487) as acrylic. The bottom acrylic window of the ![]() $20\times 15\ {\rm cm}^{2}$ cross-section and 85 cm long test section is coated with a 5 mm thick transparent compliant material made of PDMS (Dow Corning Sylgard
$20\times 15\ {\rm cm}^{2}$ cross-section and 85 cm long test section is coated with a 5 mm thick transparent compliant material made of PDMS (Dow Corning Sylgard![]() 184 Polydimethylsiloxane) mixed with a silicone softener (Sylgard
184 Polydimethylsiloxane) mixed with a silicone softener (Sylgard![]() 527) at a ratio of 1 : 7.5 to obtain a storage modulus,
527) at a ratio of 1 : 7.5 to obtain a storage modulus, ![]() $E$, of 158 kPa and loss tangent of 0.01 (Wang et al. Reference Wang, Koley and Katz2020). For the present tests, we have made a fresh compliant wall, following the Wang et al. (Reference Wang, Koley and Katz2020) recipe, including the same specific brand of PDMS and softener and the same manufacturing procedures, namely mixing ratio, curing temperature, curing time, ambient pressure, etc. We have also verified that the storage modulus and loss modulus remain unchanged, at least at low frequencies (<20 Hz) based on tests performed using Texas Instrument Q850
$E$, of 158 kPa and loss tangent of 0.01 (Wang et al. Reference Wang, Koley and Katz2020). For the present tests, we have made a fresh compliant wall, following the Wang et al. (Reference Wang, Koley and Katz2020) recipe, including the same specific brand of PDMS and softener and the same manufacturing procedures, namely mixing ratio, curing temperature, curing time, ambient pressure, etc. We have also verified that the storage modulus and loss modulus remain unchanged, at least at low frequencies (<20 Hz) based on tests performed using Texas Instrument Q850![]() dynamic mechanical analyzer. The different refractive index of the coating (1.406) is needed for measuring the wall deformation using interferometry. The boundary layer is tripped, 48 cm upstream of the measurement region, with a series of 0.5 mm high grooves to establish an equilibrium turbulent boundary layer, as confirmed by the profiles of free-stream velocity and Reynolds stresses for a smooth rigid-wall boundary layer (Wang et al. Reference Wang, Koley and Katz2020). The flow and compliant wall deformation are measured at three
dynamic mechanical analyzer. The different refractive index of the coating (1.406) is needed for measuring the wall deformation using interferometry. The boundary layer is tripped, 48 cm upstream of the measurement region, with a series of 0.5 mm high grooves to establish an equilibrium turbulent boundary layer, as confirmed by the profiles of free-stream velocity and Reynolds stresses for a smooth rigid-wall boundary layer (Wang et al. Reference Wang, Koley and Katz2020). The flow and compliant wall deformation are measured at three ![]() $Re_\tau$, ranging from 3300 to 8900, or
$Re_\tau$, ranging from 3300 to 8900, or ![]() $E/(\rho {U_0}^2)$ ranging from 2.5 to 20.3. The values of
$E/(\rho {U_0}^2)$ ranging from 2.5 to 20.3. The values of ![]() $\delta$ and
$\delta$ and ![]() $U_0$, the mean velocity outside of the boundary layer, are determined from large field-of-view stereo PIV measurements, and
$U_0$, the mean velocity outside of the boundary layer, are determined from large field-of-view stereo PIV measurements, and ![]() $\delta _\nu$ is estimated from a fit to the velocity profiles in the log layer using tomographic particle tracking velocimetry (TPTV) data. In the following discussions, (
$\delta _\nu$ is estimated from a fit to the velocity profiles in the log layer using tomographic particle tracking velocimetry (TPTV) data. In the following discussions, (![]() $x,y,z$) and (
$x,y,z$) and (![]() $u,v,w$) are the streamwise, wall-normal and spanwise directions and velocity components, respectively, with
$u,v,w$) are the streamwise, wall-normal and spanwise directions and velocity components, respectively, with ![]() $U_i$ and
$U_i$ and ![]() $u_i'$ referring to ensemble averaged and fluctuating quantities.
$u_i'$ referring to ensemble averaged and fluctuating quantities.
Simultaneous measurements of the time-resolved volumetric flow field and spatial distribution of wall deformation are performed using an integrated system involving TPTV for measuring the flow, and Mach Zehnder interferometry (MZI) for mapping the surface deformation. The system is illustrated in figure 1(a), dimensions are listed in table 1, and descriptions of components can be found in Zhang et al. (Reference Zhang, Miorini and Katz2015). For TPTV, the flow field is illuminated by a 10 mm thick laser sheet (Photonics DM60-527 ND:YLF laser) at frequencies varying between 4.5 and 8.7 kHz. The liquid is seeded with 13 ![]() $\mathrm {\mu }{\rm m}$ diameter silver-coated hollow glass spheres that have a specific gravity of 1.6, slightly lighter than the liquid (
$\mathrm {\mu }{\rm m}$ diameter silver-coated hollow glass spheres that have a specific gravity of 1.6, slightly lighter than the liquid (![]() $1850\ {\rm kg}\ {\rm m}^{-3}$). The images are recorded by four high-speed cameras (PCO Dimax S4), marked as Cam 1–4, located on both sides of the test section. Mirrors M1 and M2 are backside polished and have a reflectivity of 99.9 %. They are used as beam splitters, with the latter reflecting the light to the test section to enhance the illumination intensity. The remaining 0.1 % is transmitted through M1 and M2 to create the reference and object beams of the interferometer, respectively, and their pathlengths are matched with mirrors M4–M7. As light propagates through the compliant surface, its phase is modulated by the wall deformation, and the resulting interference pattern is recorded by a fifth high-speed camera (Phantom V2640), which is marked as Cam 5. For each
$1850\ {\rm kg}\ {\rm m}^{-3}$). The images are recorded by four high-speed cameras (PCO Dimax S4), marked as Cam 1–4, located on both sides of the test section. Mirrors M1 and M2 are backside polished and have a reflectivity of 99.9 %. They are used as beam splitters, with the latter reflecting the light to the test section to enhance the illumination intensity. The remaining 0.1 % is transmitted through M1 and M2 to create the reference and object beams of the interferometer, respectively, and their pathlengths are matched with mirrors M4–M7. As light propagates through the compliant surface, its phase is modulated by the wall deformation, and the resulting interference pattern is recorded by a fifth high-speed camera (Phantom V2640), which is marked as Cam 5. For each ![]() $Re_\tau$, data are recorded for
$Re_\tau$, data are recorded for ![]() $\sim$3 s, resulting in 13 000–26 000 frames. Specific values are provided in table 1.
$\sim$3 s, resulting in 13 000–26 000 frames. Specific values are provided in table 1.

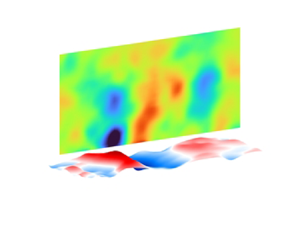
Figure 1. (a) The integrated MZI and TPTV set-up for simultaneous time-resolved measurements of the 2-D distribution of compliant wall deformation and the 3-D flow field (Zhang, Miorini & Katz Reference Zhang, Miorini and Katz2015). Sample instantaneous snapshots of wall deformation (in exaggerated scales) and pressure in the spanwise plane of maximum deformation at (b) ![]() $Re_\tau =3300$ and (c)
$Re_\tau =3300$ and (c) ![]() $Re_\tau =6700$.
$Re_\tau =6700$.
Table 1. Experimental conditions.

For flow and pressure measurements, the 3-D particle tracks are detected using the ‘Shake-The-Box’ Lagrangian tracking method based on the Lavision Davis![]() 10.2 software. Coarse calibration performed translating a target, followed by a self-calibration, give a mean tomographic disparity of 0.05 pixel and a standard deviation of 0.14 pixel. The vertical resolution is
10.2 software. Coarse calibration performed translating a target, followed by a self-calibration, give a mean tomographic disparity of 0.05 pixel and a standard deviation of 0.14 pixel. The vertical resolution is ![]() $29.6\ \mathrm {\mu }{\rm m}\ {\rm pixel}^{-1}$, corresponding to 2.2
$29.6\ \mathrm {\mu }{\rm m}\ {\rm pixel}^{-1}$, corresponding to 2.2![]() $\delta _\nu$ at the lowest
$\delta _\nu$ at the lowest ![]() $Re_\tau$, and 5.8
$Re_\tau$, and 5.8![]() $\delta _\nu$ at the highest
$\delta _\nu$ at the highest ![]() $Re_\tau$. Following Agarwal et al. (Reference Agarwal, Ram, Wang, Lu and Katz2021), the unstructured velocity and material acceleration are obtained based on polynomial fit to the particle tracks. The data are then interpolated onto a structured grid (see table 1 for spacing) using a constrained cost minimization (CCM) method, which minimizes differences from the experimental data and the previous iteration, and forces the velocity to be divergence-free, and the material acceleration curl-free away from the wall, while accounting for the viscous terms in the buffer and viscous sublayers, i.e.
$Re_\tau$. Following Agarwal et al. (Reference Agarwal, Ram, Wang, Lu and Katz2021), the unstructured velocity and material acceleration are obtained based on polynomial fit to the particle tracks. The data are then interpolated onto a structured grid (see table 1 for spacing) using a constrained cost minimization (CCM) method, which minimizes differences from the experimental data and the previous iteration, and forces the velocity to be divergence-free, and the material acceleration curl-free away from the wall, while accounting for the viscous terms in the buffer and viscous sublayers, i.e. ![]() $\nabla \times (({\rm D}\boldsymbol {u}/{\rm D}t)-\nu \nabla ^2\boldsymbol {u})=0$. The 3-D pressure distribution is calculated by spatial integration of the material acceleration (Wang, Zhang & Katz Reference Wang, Zhang and Katz2019). This integration uses a Graphics Processing Unit (GPU)-based, parallel-line, omni-directional algorithm, in which the pressure at each point is calculated by averaging integrations along paths aligned uniformly in all directions. The viscous effect is also accounted for in the near-wall region during the integration, i.e.
$\nabla \times (({\rm D}\boldsymbol {u}/{\rm D}t)-\nu \nabla ^2\boldsymbol {u})=0$. The 3-D pressure distribution is calculated by spatial integration of the material acceleration (Wang, Zhang & Katz Reference Wang, Zhang and Katz2019). This integration uses a Graphics Processing Unit (GPU)-based, parallel-line, omni-directional algorithm, in which the pressure at each point is calculated by averaging integrations along paths aligned uniformly in all directions. The viscous effect is also accounted for in the near-wall region during the integration, i.e. ![]() $\nabla p=-\rho ({\rm D}\boldsymbol {u}/{\rm D}t)+\mu \nabla ^2\boldsymbol {u}$, where
$\nabla p=-\rho ({\rm D}\boldsymbol {u}/{\rm D}t)+\mu \nabla ^2\boldsymbol {u}$, where ![]() $\rho$ and
$\rho$ and ![]() $\mu$ are the pressure field and the dynamic viscosity, respectively. Experimental errors are further reduced by assigning weights to each path that are inversely proportional to the curl of the material acceleration. After integrations, the spatially averaged pressure is set to zero, hence the pressure discussed in this paper is the deviation of instantaneous pressure from the spatially averaged value. The uncertainty analysis in Agarwal et al. (Reference Agarwal, Ram, Wang, Lu and Katz2021) shows that the r.m.s. errors for velocity and pressure are less than 0.1
$\mu$ are the pressure field and the dynamic viscosity, respectively. Experimental errors are further reduced by assigning weights to each path that are inversely proportional to the curl of the material acceleration. After integrations, the spatially averaged pressure is set to zero, hence the pressure discussed in this paper is the deviation of instantaneous pressure from the spatially averaged value. The uncertainty analysis in Agarwal et al. (Reference Agarwal, Ram, Wang, Lu and Katz2021) shows that the r.m.s. errors for velocity and pressure are less than 0.1![]() $u_\tau$ (3 %) and 0.7
$u_\tau$ (3 %) and 0.7![]() $\rho {u_\tau }^2$ (10 %) at
$\rho {u_\tau }^2$ (10 %) at ![]() $y^+>80$, respectively. At lower elevations, the velocity error increases to
$y^+>80$, respectively. At lower elevations, the velocity error increases to ![]() $\sim$6 % at
$\sim$6 % at ![]() $y^+=10$ and that of the pressure remains similar. Ensemble averaging further reduces the uncertainty by an order of magnitude.
$y^+=10$ and that of the pressure remains similar. Ensemble averaging further reduces the uncertainty by an order of magnitude.
To measure the deformation, following Zhang et al. (Reference Zhang, Miorini and Katz2015) and Zhang et al. (Reference Zhang, Wang, Blake and Katz2017), the interferogram intensity can be expressed as ![]() $I(x,z,t)=C_1(x,z,t)+2C_2(x,z,t)\cos [\varphi _0(x,z)+(2{\rm \pi} \Delta n/\lambda _0)d(x,z,t)]$, where
$I(x,z,t)=C_1(x,z,t)+2C_2(x,z,t)\cos [\varphi _0(x,z)+(2{\rm \pi} \Delta n/\lambda _0)d(x,z,t)]$, where ![]() $C_1$ and
$C_1$ and ![]() $C_2$ are the sum of wave intensities and the product of their amplitudes, respectively. The stationary term,
$C_2$ are the sum of wave intensities and the product of their amplitudes, respectively. The stationary term, ![]() $\varphi _0$, accounts for the unperturbed wavefront, and can be removed by subtracting the time-averaged phase. In the second term, which accounts for the deformation,
$\varphi _0$, accounts for the unperturbed wavefront, and can be removed by subtracting the time-averaged phase. In the second term, which accounts for the deformation, ![]() $\Delta n$ is the difference between the refractive indices of the coating and the liquid,
$\Delta n$ is the difference between the refractive indices of the coating and the liquid, ![]() $\lambda _0$ is the laser wavelength in air, and
$\lambda _0$ is the laser wavelength in air, and ![]() $d$ is the deformation height. Temporal normalization and correlation-based filtering are used for enhancing the fringes and homogenizing their peaks. The phase is determined from the arccosines, followed by unwrapping and detrending. The r.m.s. and peak uncertainty (Zhang et al. Reference Zhang, Miorini and Katz2015) in deformation are 11 and 20 nm, respectively. Consistent with Wang et al. (Reference Wang, Koley and Katz2020), the present peak deformation,
$d$ is the deformation height. Temporal normalization and correlation-based filtering are used for enhancing the fringes and homogenizing their peaks. The phase is determined from the arccosines, followed by unwrapping and detrending. The r.m.s. and peak uncertainty (Zhang et al. Reference Zhang, Miorini and Katz2015) in deformation are 11 and 20 nm, respectively. Consistent with Wang et al. (Reference Wang, Koley and Katz2020), the present peak deformation, ![]() $d_{peak}$, increases from 0.2
$d_{peak}$, increases from 0.2![]() $\delta _\nu$ to 3.5
$\delta _\nu$ to 3.5![]() $\delta _\nu$ as
$\delta _\nu$ as ![]() $Re_\tau$ increases from 3300 to 8900. The corresponding r.m.s. values,
$Re_\tau$ increases from 3300 to 8900. The corresponding r.m.s. values, ![]() $d_{rms}$, increase from 0.03 to 0.44
$d_{rms}$, increase from 0.03 to 0.44![]() $\delta _\nu$.
$\delta _\nu$.
3. Results
3.1. Surface wave characteristics and their correlations with flow parameters
Figures 1(b) and 1(c) show sample instantaneous snapshots of the surface shape along with the pressure distribution in (![]() $x,y$) planes coinciding with the deformation peaks at
$x,y$) planes coinciding with the deformation peaks at ![]() $Re_\tau =3300$ and 6700, respectively. Corresponding movies are provided as supplementary movies 1 and 2 and are available at https://doi.org/10.1017/jfm.2024.11. Note that the deformation amplitude is exaggerated in comparison with the boundary-layer scales. As expected, a pressure minimum is located above a positive deformation (‘bump’), and a maximum above a negative one (‘dimple’). At all
$Re_\tau =3300$ and 6700, respectively. Corresponding movies are provided as supplementary movies 1 and 2 and are available at https://doi.org/10.1017/jfm.2024.11. Note that the deformation amplitude is exaggerated in comparison with the boundary-layer scales. As expected, a pressure minimum is located above a positive deformation (‘bump’), and a maximum above a negative one (‘dimple’). At all ![]() $Re_\tau$, these pressure structures travel with the deformation peaks and appear to be phase locked with them, extending to well over
$Re_\tau$, these pressure structures travel with the deformation peaks and appear to be phase locked with them, extending to well over ![]() $y^+=500$, even when the deformation amplitude is very small (
$y^+=500$, even when the deformation amplitude is very small (![]() ${\sim }0.1\delta _\nu$ in figure 1b). Figure 2 presents streamwise wavenumber–frequency (
${\sim }0.1\delta _\nu$ in figure 1b). Figure 2 presents streamwise wavenumber–frequency (![]() $k_x-\omega$) spectra of the compliant surface deformation at three
$k_x-\omega$) spectra of the compliant surface deformation at three ![]() $Re_\tau$, where the wavenumber in rad/m is normalized by
$Re_\tau$, where the wavenumber in rad/m is normalized by ![]() $1/l_0$ and the frequency in
$1/l_0$ and the frequency in ![]() ${\rm rad}\ {\rm s}^{-1}$ by
${\rm rad}\ {\rm s}^{-1}$ by ![]() $U_0/l_0$, with
$U_0/l_0$, with ![]() $l_{0}$ being the compliant material thickness. The spectra are calculated using the 2-D fast Fourier transform function in Matlab
$l_{0}$ being the compliant material thickness. The spectra are calculated using the 2-D fast Fourier transform function in Matlab![]() based on the entire database for each streamwise line, and then averaged in the spanwise direction. While the spectral peaks are located near the edge of the present wavenumber range, they correspond to a wavelength of 3
based on the entire database for each streamwise line, and then averaged in the spanwise direction. While the spectral peaks are located near the edge of the present wavenumber range, they correspond to a wavelength of 3![]() $l_0$, i.e. they do not vary with
$l_0$, i.e. they do not vary with ![]() $Re_\tau$, in agreement with the prediction of the Chase (Reference Chase1991) model and the experimental data by Wang et al. (Reference Wang, Koley and Katz2020). Yet, being centred around
$Re_\tau$, in agreement with the prediction of the Chase (Reference Chase1991) model and the experimental data by Wang et al. (Reference Wang, Koley and Katz2020). Yet, being centred around ![]() $\omega l_0/U_0\sim 1.1$, the corresponding frequency increases with
$\omega l_0/U_0\sim 1.1$, the corresponding frequency increases with ![]() $Re_\tau$. All the spectra contain a primary band indicating an advection speed of
$Re_\tau$. All the spectra contain a primary band indicating an advection speed of ![]() $U_{sw}=0.53U_0$, and a secondary wave, which is
$U_{sw}=0.53U_0$, and a secondary wave, which is ![]() $2\ {\rm to}\ 3$ orders of magnitude weaker, that is advected at approximately 0.9
$2\ {\rm to}\ 3$ orders of magnitude weaker, that is advected at approximately 0.9![]() $U_0$. The latter is reported also in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017), but not in Wang et al. (Reference Wang, Koley and Katz2020), and owing to its small amplitude, the rest of the discussion focuses on the primary band. Prior studies of compliant wall boundary layers have reported advection speeds that scale with
$U_0$. The latter is reported also in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017), but not in Wang et al. (Reference Wang, Koley and Katz2020), and owing to its small amplitude, the rest of the discussion focuses on the primary band. Prior studies of compliant wall boundary layers have reported advection speeds that scale with ![]() $U_0$, with coefficients varying between 0.4 and 0.8, e.g. 0.40 in Kim & Choi (Reference Kim and Choi2014), 0.50 in Gad-el Hak (Reference Gad-el Hak1986b), 0.53 in the present data, 0.65 in Esteghamatian et al. (Reference Esteghamatian, Katz and Zaki2022), 0.66 in Wang et al. (Reference Wang, Koley and Katz2020), 0.70 in Dixon, Lucey & Carpenter (Reference Dixon, Lucey and Carpenter1994), 0.72 in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) and 0.70–0.80 in Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022). Combining the entire data does not show persistent trends with material stiffness, density, thickness and Reynolds number. There are conflicts in the reported trends, e.g. measurements performed in our laboratory suggest an increase in
$U_0$, with coefficients varying between 0.4 and 0.8, e.g. 0.40 in Kim & Choi (Reference Kim and Choi2014), 0.50 in Gad-el Hak (Reference Gad-el Hak1986b), 0.53 in the present data, 0.65 in Esteghamatian et al. (Reference Esteghamatian, Katz and Zaki2022), 0.66 in Wang et al. (Reference Wang, Koley and Katz2020), 0.70 in Dixon, Lucey & Carpenter (Reference Dixon, Lucey and Carpenter1994), 0.72 in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) and 0.70–0.80 in Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022). Combining the entire data does not show persistent trends with material stiffness, density, thickness and Reynolds number. There are conflicts in the reported trends, e.g. measurements performed in our laboratory suggest an increase in ![]() $U_{sw}/U_0$ with increasing stiffness, while Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022) show a slight decrease. Trends with thickness also vary, with Kim & Choi (Reference Kim and Choi2014) and Gad-el Hak (Reference Gad-el Hak1986b) reporting a decrease in speed with increasing thickness. Conversely, in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017)
$U_{sw}/U_0$ with increasing stiffness, while Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022) show a slight decrease. Trends with thickness also vary, with Kim & Choi (Reference Kim and Choi2014) and Gad-el Hak (Reference Gad-el Hak1986b) reporting a decrease in speed with increasing thickness. Conversely, in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) ![]() $U_{sw}/U_0=0.72$ for
$U_{sw}/U_0=0.72$ for ![]() $l_0=16$ mm matches the Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022) values for
$l_0=16$ mm matches the Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022) values for ![]() $l_0=5$ mm, but not those of Wang et al. (Reference Wang, Koley and Katz2020) and the current data for the same thickness. Effects of density ratio and shear speed are also inconsistent. Even for the same set-up and material in our laboratory, the present value is lower than that in Wang et al. (Reference Wang, Koley and Katz2020). The only difference is the lower turbulence and large-scale fluctuations in the free-stream conditions. This unresolved topic is deferred to future studies, and might benefit from systematic numerical simulations.
$l_0=5$ mm, but not those of Wang et al. (Reference Wang, Koley and Katz2020) and the current data for the same thickness. Effects of density ratio and shear speed are also inconsistent. Even for the same set-up and material in our laboratory, the present value is lower than that in Wang et al. (Reference Wang, Koley and Katz2020). The only difference is the lower turbulence and large-scale fluctuations in the free-stream conditions. This unresolved topic is deferred to future studies, and might benefit from systematic numerical simulations.

Figure 2. Streamwise wavenumber–frequency spectra of surface deformation for the following ![]() $Re_\tau$ and
$Re_\tau$ and ![]() $E/(\rho {U_0}^2)$, respectively: (a) 3300,20.3; (b) 6700,4.5; and (c) 8900,2.5.
$E/(\rho {U_0}^2)$, respectively: (a) 3300,20.3; (b) 6700,4.5; and (c) 8900,2.5.
The next discussion involves conditional statistics based on deformation magnitude, namely ![]() $d>\sigma _d$ for a bump and
$d>\sigma _d$ for a bump and ![]() $d<-\sigma _d$ for a dimple (
$d<-\sigma _d$ for a dimple (![]() $\sigma _d$ is the standard deviation), aimed at elucidating the relationship between deformation and the pressure, velocity and vorticity fields. Figures 3(a) and 3(b) show the planar surface pattern conditioned on a bump and a dimple, respectively. The spatial conditional correlations between flow variable
$\sigma _d$ is the standard deviation), aimed at elucidating the relationship between deformation and the pressure, velocity and vorticity fields. Figures 3(a) and 3(b) show the planar surface pattern conditioned on a bump and a dimple, respectively. The spatial conditional correlations between flow variable ![]() $f(x,y,z,t)$ and
$f(x,y,z,t)$ and ![]() $d(x,y,z,t)$ for a bump (for example) is defined as
$d(x,y,z,t)$ for a bump (for example) is defined as ![]() $\widetilde {C_{f-d}}(\Delta x,y,\Delta z)|_{d>\sigma _d}=\langle \,f(x_0+\Delta x,y,z_0+\Delta z,t)d(x_0,z_0,t)\rangle$
$\widetilde {C_{f-d}}(\Delta x,y,\Delta z)|_{d>\sigma _d}=\langle \,f(x_0+\Delta x,y,z_0+\Delta z,t)d(x_0,z_0,t)\rangle$ ![]() $|_{d>\sigma _d}/[\sigma _f(x_0+\Delta x,y,z_0+\Delta z,t)\sigma _d(x_0,z_0,t)]|_{d>\sigma _d}$. These correlations are computed at 3552 points on the compliant wall and then spatially and ensemble averaged. Results for
$|_{d>\sigma _d}/[\sigma _f(x_0+\Delta x,y,z_0+\Delta z,t)\sigma _d(x_0,z_0,t)]|_{d>\sigma _d}$. These correlations are computed at 3552 points on the compliant wall and then spatially and ensemble averaged. Results for ![]() $\widetilde {C_{p'-d}}$ at
$\widetilde {C_{p'-d}}$ at ![]() $Re_\tau =3300$, which also include selected in-plane streamlines, are presented in figures 3(c) and 3(d) under the corresponding surface shapes. Maps of
$Re_\tau =3300$, which also include selected in-plane streamlines, are presented in figures 3(c) and 3(d) under the corresponding surface shapes. Maps of ![]() $\widetilde {C_{u'-d}}$,
$\widetilde {C_{u'-d}}$, ![]() $\widetilde {C_{v'-d}}$, along with the conditionally averaged vertical vorticity,
$\widetilde {C_{v'-d}}$, along with the conditionally averaged vertical vorticity, ![]() $\widetilde {{\omega _y}^{'+}}$ and in-plane velocity vectors at
$\widetilde {{\omega _y}^{'+}}$ and in-plane velocity vectors at ![]() $y^+=120$ are provided in supplementary figures S1(a–f). As is evident, the bump is bounded by dimples located on both sides and vice versa, and the characteristic wavelength is 2.8
$y^+=120$ are provided in supplementary figures S1(a–f). As is evident, the bump is bounded by dimples located on both sides and vice versa, and the characteristic wavelength is 2.8![]() $l_0$, close to 3
$l_0$, close to 3![]() $l_0$, as predicted by the Chase (Reference Chase1991) model. The in-plane streamlines indicate that the bump is located under a spanwise vortex, and the dimple under the transition between ‘sweeping’ and ‘ejection’ events, downstream of the vortex. The velocity-deformation correlations peak in the sweeping flow region between the bump and the dimple, where the flow is induced, at least in part, by the vortex, but not necessarily in the same
$l_0$, as predicted by the Chase (Reference Chase1991) model. The in-plane streamlines indicate that the bump is located under a spanwise vortex, and the dimple under the transition between ‘sweeping’ and ‘ejection’ events, downstream of the vortex. The velocity-deformation correlations peak in the sweeping flow region between the bump and the dimple, where the flow is induced, at least in part, by the vortex, but not necessarily in the same ![]() $\Delta x$. This vortex has a limited spanwise extent, approximately 400
$\Delta x$. This vortex has a limited spanwise extent, approximately 400![]() $\delta _\nu$ (not shown), with lateral flow converging from both sides towards
$\delta _\nu$ (not shown), with lateral flow converging from both sides towards ![]() $\Delta z=0$ (figure S1e). Once the sweeping flow impinges on the surface, the lateral flow diverges outward (figure S1f). The
$\Delta z=0$ (figure S1e). Once the sweeping flow impinges on the surface, the lateral flow diverges outward (figure S1f). The ![]() $\widetilde {{\omega _y}^{'+}}$ maps show signatures of multiple counter-rotating, quasi-streamwise vortex pairs, with the peaks corresponding to a pair that generates a downward flow at
$\widetilde {{\omega _y}^{'+}}$ maps show signatures of multiple counter-rotating, quasi-streamwise vortex pairs, with the peaks corresponding to a pair that generates a downward flow at ![]() $\Delta z=0$ (opposite to a hairpin vortex). The
$\Delta z=0$ (opposite to a hairpin vortex). The ![]() $\widetilde {C_{p'-d}}$ peak for the bump is located slightly downstream of the spanwise vortex, at
$\widetilde {C_{p'-d}}$ peak for the bump is located slightly downstream of the spanwise vortex, at ![]() ${\Delta x}^+=30$, and
${\Delta x}^+=30$, and ![]() ${\Delta y}^+=90$, and its magnitude,
${\Delta y}^+=90$, and its magnitude, ![]() $-0.8$ (figure 3c), indicates that the pressure plays a primary role. There is also a slight shift of
$-0.8$ (figure 3c), indicates that the pressure plays a primary role. There is also a slight shift of ![]() ${\Delta x}^+=30$ between the dimple and the location of minimum correlation at the sweep-ejection transition (figure 3d). Weaker positive peaks are located on both sides of the bump, corresponding to the high pressures above dimples, and vice versa. Above the bump, the pressure minimum is associated with both the spanwise vortex and the lateral acceleration, and above the dimple the pressure maximum is associated with lateral deceleration and inherent maximum at the sweep-ejection transition (Kim Reference Kim1983). Before concluding this section, one should note that unlike the conditionally averaged flow field, many instantaneous realizations only contain fractions of the 3-D flow structures depicted in figure S1, e.g. an isolated spanwise vortex, or a quasi-streamwise vortex located on one of the sides of the bump.
${\Delta x}^+=30$ between the dimple and the location of minimum correlation at the sweep-ejection transition (figure 3d). Weaker positive peaks are located on both sides of the bump, corresponding to the high pressures above dimples, and vice versa. Above the bump, the pressure minimum is associated with both the spanwise vortex and the lateral acceleration, and above the dimple the pressure maximum is associated with lateral deceleration and inherent maximum at the sweep-ejection transition (Kim Reference Kim1983). Before concluding this section, one should note that unlike the conditionally averaged flow field, many instantaneous realizations only contain fractions of the 3-D flow structures depicted in figure S1, e.g. an isolated spanwise vortex, or a quasi-streamwise vortex located on one of the sides of the bump.

Figure 3. Conditional statistics for a surface bump (a,c) and a dimple (b,d), both for ![]() $Re_\tau =3300$: (a,b) wall shape, and (c,d)
$Re_\tau =3300$: (a,b) wall shape, and (c,d) ![]() $p'-d$ correlation superimposed on conditional streamlines.
$p'-d$ correlation superimposed on conditional streamlines.
The next point of discussion involves scaling the deformation height based on flow parameters and material properties, combining the present data with those of Zhang et al. (Reference Zhang, Wang, Blake and Katz2017), Wang et al. (Reference Wang, Koley and Katz2020) and Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022). The materials used by Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022) are softer than the present ones, and that used by Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) is an order of magnitude harder. Two methods are used to estimate the r.m.s. pressure: in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) and for the present data, we integrate the material acceleration; for the rest, following Benschop et al. (Reference Benschop, Greidanus, Delfos, Westerweel and Breugem2019), the r.m.s. pressure is estimated using the empirical model introduced by Goody (Reference Goody2002), namely ![]() $(\,p'_{rms}/(\rho {u_\tau }^2))^2=0.0309+0.745[\ln ({u_\tau }^2\delta /(U_0\nu))]^2$. To assess the compatibility of these methods, the model prediction for the present data, labelled ‘Present-empirical’, is compared with the ‘Present-measured’ values. In figure 4(a), the pressure is normalized by
$(\,p'_{rms}/(\rho {u_\tau }^2))^2=0.0309+0.745[\ln ({u_\tau }^2\delta /(U_0\nu))]^2$. To assess the compatibility of these methods, the model prediction for the present data, labelled ‘Present-empirical’, is compared with the ‘Present-measured’ values. In figure 4(a), the pressure is normalized by ![]() $G=\rho _s {c_t}^2$, where
$G=\rho _s {c_t}^2$, where ![]() $G$,
$G$, ![]() $\rho _s$ and
$\rho _s$ and ![]() $c_t$ are the shear modulus, density and shear speed of the elastomer, respectively. When
$c_t$ are the shear modulus, density and shear speed of the elastomer, respectively. When ![]() $d_{rms}$ is normalized by
$d_{rms}$ is normalized by ![]() $\delta _\nu$ (
$\delta _\nu$ (![]() ${d_{rms}}^+$), trends of Zhang et al. (Reference Zhang, Wang, Blake and Katz2017), Wang et al. (Reference Wang, Zhang and Katz2019), and the present data do not agree with those in Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022). While the measured pressure is lower than the modelled values by 1.3 to 1.8, they still follow similar trends, hence the discrepancy in
${d_{rms}}^+$), trends of Zhang et al. (Reference Zhang, Wang, Blake and Katz2017), Wang et al. (Reference Wang, Zhang and Katz2019), and the present data do not agree with those in Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022). While the measured pressure is lower than the modelled values by 1.3 to 1.8, they still follow similar trends, hence the discrepancy in ![]() ${d_{rms}}^+$ is not caused by Goody's (Reference Goody2002) empirical pressure estimate. In contrast, if the same data are plotted with the deformation scaled by the wall thickness, following Benschop et al. (Reference Benschop, Greidanus, Delfos, Westerweel and Breugem2019) and Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022), the results collapse, as demonstrated in figure 4(b). This agreement includes the Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) data that has a different thickness (16 mm). The least-square-fitted power relationship excludes the data points at
${d_{rms}}^+$ is not caused by Goody's (Reference Goody2002) empirical pressure estimate. In contrast, if the same data are plotted with the deformation scaled by the wall thickness, following Benschop et al. (Reference Benschop, Greidanus, Delfos, Westerweel and Breugem2019) and Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022), the results collapse, as demonstrated in figure 4(b). This agreement includes the Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) data that has a different thickness (16 mm). The least-square-fitted power relationship excludes the data points at ![]() $p'_{rms}/(\rho _s{c_t}^2)>0.076$ (shaded region in figure 4b), which according to Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022), fall in the nonlinear response range, where unstable waves develop on the compliant surface. The resulting empirical relation,
$p'_{rms}/(\rho _s{c_t}^2)>0.076$ (shaded region in figure 4b), which according to Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022), fall in the nonlinear response range, where unstable waves develop on the compliant surface. The resulting empirical relation, ![]() $d_{rms}/l_0=0.05(\,p'_{rms}/(\rho _s{c_t}^2))^{0.98}$, covers more than two orders of magnitude of
$d_{rms}/l_0=0.05(\,p'_{rms}/(\rho _s{c_t}^2))^{0.98}$, covers more than two orders of magnitude of ![]() $p'_{rms}/(\rho _s{c_t}^2)$ and three orders of magnitude of
$p'_{rms}/(\rho _s{c_t}^2)$ and three orders of magnitude of ![]() $d_{rms}/l_0$. This nearly linear relationship is consistent with the theoretical model introduced in Benschop et al. (Reference Benschop, Greidanus, Delfos, Westerweel and Breugem2019) and the data presented in Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022). Note that Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022) provides many more data points for the range of their results, but we only include a sample of them to maintain a similar weight to data obtained from other sources. Furthermore, the linear relationship could be interpreted as the longitudinal strain
$d_{rms}/l_0$. This nearly linear relationship is consistent with the theoretical model introduced in Benschop et al. (Reference Benschop, Greidanus, Delfos, Westerweel and Breugem2019) and the data presented in Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022). Note that Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022) provides many more data points for the range of their results, but we only include a sample of them to maintain a similar weight to data obtained from other sources. Furthermore, the linear relationship could be interpreted as the longitudinal strain ![]() $\sim d_{rms}/l_0$ being proportional to the stress divided by the storage modulus, given that
$\sim d_{rms}/l_0$ being proportional to the stress divided by the storage modulus, given that ![]() $G=E/[2(1+\eta )]$, with
$G=E/[2(1+\eta )]$, with ![]() $\eta$ being the Poisson ratio. For
$\eta$ being the Poisson ratio. For ![]() $\eta =0.5$, the relationship becomes
$\eta =0.5$, the relationship becomes ![]() $d_{rms}/l_0\sim 0.15(\,p'_{rms}/E)$. The only parameter related to the flow is
$d_{rms}/l_0\sim 0.15(\,p'_{rms}/E)$. The only parameter related to the flow is ![]() $p'_{rms}$. It should be emphasized that the trends depicted in figure 4(b) are likely to change as the compliant wall thickness becomes very large, and consequently, the interactions with the rigid wall under it diminish. Indeed, the theoretical analysis of wall response to harmonic excitation by Benschop et al. (Reference Benschop, Greidanus, Delfos, Westerweel and Breugem2019) shows that when the compliant material thickness is much larger than the excitation wavelength, the deformation height becomes independent of
$p'_{rms}$. It should be emphasized that the trends depicted in figure 4(b) are likely to change as the compliant wall thickness becomes very large, and consequently, the interactions with the rigid wall under it diminish. Indeed, the theoretical analysis of wall response to harmonic excitation by Benschop et al. (Reference Benschop, Greidanus, Delfos, Westerweel and Breugem2019) shows that when the compliant material thickness is much larger than the excitation wavelength, the deformation height becomes independent of ![]() $l_0$, hence
$l_0$, hence ![]() $d_{rms}/l_0$ diminishes.
$d_{rms}/l_0$ diminishes.

Figure 4. The r.m.s. of surface deformation scaled as (a) ![]() ${d_{rms}}^+$, and (b)
${d_{rms}}^+$, and (b) ![]() $d_{rms}/l_0$ plotted vs pressure fluctuations r.m.s. normalized by the shear modulus using data originated from several sources. The ‘Present-measured’ and Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) data for
$d_{rms}/l_0$ plotted vs pressure fluctuations r.m.s. normalized by the shear modulus using data originated from several sources. The ‘Present-measured’ and Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) data for ![]() $p'_{rms}$ are based on integration of material acceleration. The values for Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022), ‘Present-empirical’, and Wang et al. (Reference Wang, Koley and Katz2020) are estimated using Goody's (Reference Goody2002) empirical model
$p'_{rms}$ are based on integration of material acceleration. The values for Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022), ‘Present-empirical’, and Wang et al. (Reference Wang, Koley and Katz2020) are estimated using Goody's (Reference Goody2002) empirical model ![]() $(\,p'_{rms}/\rho {u_\tau }^2)^2=0.0309+0.745[\ln ({u_\tau }^2\delta /U_0\nu )]^2$.
$(\,p'_{rms}/\rho {u_\tau }^2)^2=0.0309+0.745[\ln ({u_\tau }^2\delta /U_0\nu )]^2$.
3.2. Critical layer and near-wall turbulence
The following discussion focuses on the effect of the critical layer, where ![]() $U(y)=U_{sw}$ on the structure of near-wall turbulence. The critical heights are provided in table 1 and marked in figure 5(a), along with profiles of
$U(y)=U_{sw}$ on the structure of near-wall turbulence. The critical heights are provided in table 1 and marked in figure 5(a), along with profiles of ![]() $U(y)$ obtained using sum-of-correlation (SOC) with
$U(y)$ obtained using sum-of-correlation (SOC) with ![]() $4\times 4$ pixel interrogation windows and 2-D projection of the 3-D data. Owing to the vertical resolution of the data,
$4\times 4$ pixel interrogation windows and 2-D projection of the 3-D data. Owing to the vertical resolution of the data, ![]() $118\ \mathrm {\mu }{\rm m}$/interrogation height, the present measurements do not resolve the inner part of the boundary layers. Consequently, we also add sample SOC data based on 2-D PIV from Wang et al. (Reference Wang, Koley and Katz2020) for
$118\ \mathrm {\mu }{\rm m}$/interrogation height, the present measurements do not resolve the inner part of the boundary layers. Consequently, we also add sample SOC data based on 2-D PIV from Wang et al. (Reference Wang, Koley and Katz2020) for ![]() $Re_\tau =8600$ that has been recorded at the same set-up. Figures 5(b)–5(g) present
$Re_\tau =8600$ that has been recorded at the same set-up. Figures 5(b)–5(g) present ![]() $k_x-\omega$ auto spectra of pressure,
$k_x-\omega$ auto spectra of pressure, ![]() $E_{pp}$, as well as vertical,
$E_{pp}$, as well as vertical, ![]() $E_{vv}$, and horizontal,
$E_{vv}$, and horizontal, ![]() $E_{uu}$, velocity fluctuations at
$E_{uu}$, velocity fluctuations at ![]() $Re_\tau =3300$. The upper row provides results for
$Re_\tau =3300$. The upper row provides results for ![]() $y< y_c$, and the lower row, for
$y< y_c$, and the lower row, for ![]() $y>y_c$, with the solid and dashed lines indicating
$y>y_c$, with the solid and dashed lines indicating ![]() $U_{sw}$ and
$U_{sw}$ and ![]() $U(y)$, respectively. As is evident, at
$U(y)$, respectively. As is evident, at ![]() $y< y_c$, the slopes of the advection bands in
$y< y_c$, the slopes of the advection bands in ![]() $E_{pp}$ and
$E_{pp}$ and ![]() $E_{vv}$ are equal to
$E_{vv}$ are equal to ![]() $U_{sw}$, i.e. the turbulence is advected with the deformation instead of the local flow. In
$U_{sw}$, i.e. the turbulence is advected with the deformation instead of the local flow. In ![]() $E_{uu}$, the advection band is wide and seems to be scale-dependent, being closer to
$E_{uu}$, the advection band is wide and seems to be scale-dependent, being closer to ![]() $U(y)$ at low
$U(y)$ at low ![]() $k_x$ but tilting towards
$k_x$ but tilting towards ![]() $U_{sw}$ with increasing
$U_{sw}$ with increasing ![]() $k_x$. In contrast, at
$k_x$. In contrast, at ![]() $y>y_c$, all the bands indicate advection at
$y>y_c$, all the bands indicate advection at ![]() $U(y)$, suggesting diminishing interactions with the wall motion. Using least-square fits to the bands, the advection speeds of
$U(y)$, suggesting diminishing interactions with the wall motion. Using least-square fits to the bands, the advection speeds of ![]() $p'$,
$p'$, ![]() $v'$ and
$v'$ and ![]() $u'$ as a function of
$u'$ as a function of ![]() $y/y_c$ are plotted and compared with
$y/y_c$ are plotted and compared with ![]() $U(y)$ and
$U(y)$ and ![]() $U_{sw}$ in figures 5(h)–5(j). For all three
$U_{sw}$ in figures 5(h)–5(j). For all three ![]() $Re_\tau$, the advection speeds of
$Re_\tau$, the advection speeds of ![]() $p'$ and
$p'$ and ![]() $v'$ are equal to
$v'$ are equal to ![]() $U_{sw}$ over the entire
$U_{sw}$ over the entire ![]() $y/y_c<1$ regions, changing to
$y/y_c<1$ regions, changing to ![]() $U(y)$ at
$U(y)$ at ![]() $y/y_c>1$. The advection speeds of
$y/y_c>1$. The advection speeds of ![]() $u'$ also follow
$u'$ also follow ![]() $U(y)$ at
$U(y)$ at ![]() $y/y_c>1$ but fall between
$y/y_c>1$ but fall between ![]() $U(y)$ and
$U(y)$ and ![]() $U_{sw}$ at
$U_{sw}$ at ![]() $y/y_c<1$. Furthermore, the vertical profiles of maximum
$y/y_c<1$. Furthermore, the vertical profiles of maximum ![]() $\widetilde {C_{p'-d}}$, plotted in figure 5(k), indicate that the peak pressure–deformation correlation occurs at or slightly higher than
$\widetilde {C_{p'-d}}$, plotted in figure 5(k), indicate that the peak pressure–deformation correlation occurs at or slightly higher than ![]() $y=y_c$. Revisiting Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) for a stiffer wall, they also observe a peak in
$y=y_c$. Revisiting Zhang et al. (Reference Zhang, Wang, Blake and Katz2017) for a stiffer wall, they also observe a peak in ![]() $\widetilde {C_{p'-d}}$ slightly above
$\widetilde {C_{p'-d}}$ slightly above ![]() $y=y_c$. The high correlation peaks, 0.7–0.8, suggest that the pressure and deformations are phase locked, consistent with the direct observations and with measured coherence spectra (supplementary figure S2). Note that the correlation peak in figure 5(k) is slightly higher than
$y=y_c$. The high correlation peaks, 0.7–0.8, suggest that the pressure and deformations are phase locked, consistent with the direct observations and with measured coherence spectra (supplementary figure S2). Note that the correlation peak in figure 5(k) is slightly higher than ![]() $y_c$, but the coherence peak in figure S2 is located at
$y_c$, but the coherence peak in figure S2 is located at ![]() $y_c$. Since the coherence is based on pressure–deformation cross-spectra, it only accounts for the part of the turbulence spectrum that is coherent with the wave. In contrast, the correlation includes, in addition to the coherent part, contributions from turbulence that is not coherent with the wave. As a result, the
$y_c$. Since the coherence is based on pressure–deformation cross-spectra, it only accounts for the part of the turbulence spectrum that is coherent with the wave. In contrast, the correlation includes, in addition to the coherent part, contributions from turbulence that is not coherent with the wave. As a result, the ![]() $p'-d$ correlation peaks at a higher elevation than that of the coherent part. Considering that for some of the cases, the amplitude of wall motion is an order of magnitude smaller than the wall unit, these findings are striking. For example, the wall-normal extent of the region where the turbulence (especially the pressure) is highly correlated and advected with the wave expands from 63
$p'-d$ correlation peaks at a higher elevation than that of the coherent part. Considering that for some of the cases, the amplitude of wall motion is an order of magnitude smaller than the wall unit, these findings are striking. For example, the wall-normal extent of the region where the turbulence (especially the pressure) is highly correlated and advected with the wave expands from 63![]() $\delta _\nu$ at the lowest
$\delta _\nu$ at the lowest ![]() $Re_\tau$, when
$Re_\tau$, when ![]() ${d_{rms}}^+=0.03$ (
${d_{rms}}^+=0.03$ (![]() ${d_{peak}}^+=0.22$), to nearly 200
${d_{peak}}^+=0.22$), to nearly 200![]() $\delta _\nu$, when
$\delta _\nu$, when ![]() ${d_{rms}}^+=0.44$ (
${d_{rms}}^+=0.44$ (![]() ${d_{rms}}^+=3.46$).
${d_{rms}}^+=3.46$).

Figure 5. (a) Mean velocity profiles based on the present and 2-D PIV data of Wang et al. (Reference Wang, Koley and Katz2020), and corresponding critical heights in the present data. (b–g) Streamwise wavenumber–frequency spectra, ![]() $E_{ff}$, at
$E_{ff}$, at ![]() $Re_\tau =3300$: (b,e)
$Re_\tau =3300$: (b,e) ![]() $E_{pp}/[(\rho {u_\tau }^2\delta )^2/U_0]$; (c,f)
$E_{pp}/[(\rho {u_\tau }^2\delta )^2/U_0]$; (c,f) ![]() $E_{vv}/[(u_\tau \delta )^2/U_0]$; and (d,g)
$E_{vv}/[(u_\tau \delta )^2/U_0]$; and (d,g) ![]() $E_{uu}/[(u_\tau \delta )^2/U_0]$. In (b–d)
$E_{uu}/[(u_\tau \delta )^2/U_0]$. In (b–d) ![]() $y/\delta =0.009$, i.e.
$y/\delta =0.009$, i.e. ![]() $y< y_c$, and in (e–g)
$y< y_c$, and in (e–g) ![]() $y/\delta =0.09$, i.e.
$y/\delta =0.09$, i.e. ![]() $y> y_c$. (h–j) Profiles of advection speeds of (h)
$y> y_c$. (h–j) Profiles of advection speeds of (h) ![]() $p'$, (i)
$p'$, (i) ![]() $v'$, (j)
$v'$, (j) ![]() $u'$. Solid lines ——
$u'$. Solid lines —— ![]() $U(y)/U_0$; dashed lines
$U(y)/U_0$; dashed lines ![]() $\cdots \cdots$
$\cdots \cdots$ ![]() $U_{sw}$. (k) Profiles of
$U_{sw}$. (k) Profiles of ![]() $p'-d$ correlation.
$p'-d$ correlation.
One may question whether the change in the near-wall advection speed is inherent to the inner part of turbulent boundary layers. Indeed, for channel flows over rigid smooth walls, DNS at ![]() $Re_\tau =180$ (Kim & Hussain Reference Kim and Hussain1993), and experiments performed at
$Re_\tau =180$ (Kim & Hussain Reference Kim and Hussain1993), and experiments performed at ![]() $Re_\tau =550$ (Schewe Reference Schewe1983) have shown that the advection speed at
$Re_\tau =550$ (Schewe Reference Schewe1983) have shown that the advection speed at ![]() $y^+\leq 20$ is equal to
$y^+\leq 20$ is equal to ![]() $U(y^+=20)$ for the pressure, and
$U(y^+=20)$ for the pressure, and ![]() $U(y^+=15)$ for the velocity at
$U(y^+=15)$ for the velocity at ![]() $y^+\leq 15$. Using the DNS data at
$y^+\leq 15$. Using the DNS data at ![]() $Re_\tau =1000$ available in Johns Hopkins Turbulence Database (Graham et al. Reference Graham2016), and obtaining the advection speed from the
$Re_\tau =1000$ available in Johns Hopkins Turbulence Database (Graham et al. Reference Graham2016), and obtaining the advection speed from the ![]() $k_x-\omega$ spectra, the trends agree with those of Kim & Hussain (Reference Kim and Hussain1993), including the heights below which the advection speeds are constant. Kim (Reference Kim1989) attributes these phenomena to the effect of quasi-streamwise vortices centred at
$k_x-\omega$ spectra, the trends agree with those of Kim & Hussain (Reference Kim and Hussain1993), including the heights below which the advection speeds are constant. Kim (Reference Kim1989) attributes these phenomena to the effect of quasi-streamwise vortices centred at ![]() $y^+=20$. In contrast, for the compliant wall, below the critical layer the wavelength and advection speed of pressure and vertical velocity events are equal to those of the compliant surface wave, with
$y^+=20$. In contrast, for the compliant wall, below the critical layer the wavelength and advection speed of pressure and vertical velocity events are equal to those of the compliant surface wave, with ![]() $U_{sw}$ being significantly higher than
$U_{sw}$ being significantly higher than ![]() $U(y^+=20)$. Furthermore, the turbulence and wave are phase locked and highly correlated even for
$U(y^+=20)$. Furthermore, the turbulence and wave are phase locked and highly correlated even for ![]() ${d_{rms}}^+\ll 1$. The height of this layer increases with increasing
${d_{rms}}^+\ll 1$. The height of this layer increases with increasing ![]() $Re_\tau$ extending deep into the log layer. Interestingly,
$Re_\tau$ extending deep into the log layer. Interestingly, ![]() ${y_c}^+$ is prescribed predominantly by the surface wave speed and would be nearly constant if not for modifications to the velocity profile caused by the deformation. In fact, as demonstrated in table 1, while
${y_c}^+$ is prescribed predominantly by the surface wave speed and would be nearly constant if not for modifications to the velocity profile caused by the deformation. In fact, as demonstrated in table 1, while ![]() ${y_c}^+$ increases significantly with
${y_c}^+$ increases significantly with ![]() $Re_\tau$, when
$Re_\tau$, when ![]() $y_c$ is scaled with the boundary-layer thickness,
$y_c$ is scaled with the boundary-layer thickness, ![]() $y_c/\delta$ fluctuates slightly and non-monotonically between 0.019 and 0.025. Since both
$y_c/\delta$ fluctuates slightly and non-monotonically between 0.019 and 0.025. Since both ![]() $y_c/\delta$ and
$y_c/\delta$ and ![]() $U_{sw}/U_0$ are nearly constant, both appear to be related to outer layer parameters, and the expansion of the zone with strong turbulence-deformation coupling is associated with the downward shift of the mean velocity profile in the log layer.
$U_{sw}/U_0$ are nearly constant, both appear to be related to outer layer parameters, and the expansion of the zone with strong turbulence-deformation coupling is associated with the downward shift of the mean velocity profile in the log layer.
3.3. Wall stress and mean velocity profile
An important question remains about whether the increase of friction drag, as indicated from the downward shift of the mean velocity profile, can be related to the surface ‘roughness’. Wang et al. (Reference Wang, Koley and Katz2020) provide direct comparisons between velocity profiles for a smooth rigid wall and a compliant wall at the same conditions (location in the tunnel, speed, tripping, etc.). The results show that for the entire range of Reynolds numbers, the compliant wall increases the wall shear stress by an amount that increases with deformation height. The significant drag increase, in spite of the small deformation amplitude, is most likely associated with dynamic interactions between the compliant wall and the flow, which affect both the form drag and the Reynolds stress at the wall. Hence the impact of the compliant wall should not be viewed as a roughness effect. As the shape of the wall changes, the pressure drag fluctuates spatially and temporally, and have alternate signs on the windward and leeward sides of the surface wave. Based on DNS data, Esteghamatian et al. (Reference Esteghamatian, Katz and Zaki2022) show the net effect is an increase in drag. Furthermore, the wall motion forces the flow vertically through the ![]() $\langle \,p'v'\rangle$ correlations. Also, because of the wall motion, the Reynold shear stress does not diminish at the wall. Since the wave speed is higher than the flow speed below the critical layer, the Reynolds shear stress is likely to be negative, as confirmed in the DNS by Rosti & Brandt (Reference Rosti and Brandt2017) and Esteghamatian et al. (Reference Esteghamatian, Katz and Zaki2022). Unfortunately, the spatial resolution of our measurements is insufficient for evaluating the pressure–velocity correlations, and the non-zero shear stress at the wall.
$\langle \,p'v'\rangle$ correlations. Also, because of the wall motion, the Reynold shear stress does not diminish at the wall. Since the wave speed is higher than the flow speed below the critical layer, the Reynolds shear stress is likely to be negative, as confirmed in the DNS by Rosti & Brandt (Reference Rosti and Brandt2017) and Esteghamatian et al. (Reference Esteghamatian, Katz and Zaki2022). Unfortunately, the spatial resolution of our measurements is insufficient for evaluating the pressure–velocity correlations, and the non-zero shear stress at the wall.
Before concluding, it would be of interest to examine the possible connection between the critical layer height and the Reynold stress profiles in the boundary layer. Morrill-Winter, Philip & Klewicki (Reference Morrill-Winter, Philip and Klewicki2017) report that for a smooth rigid-wall boundary layer, the elevation of the Reynolds shear stress peak is ![]() ${y_m}^+\sim 2\sqrt {\delta ^+}$. While we do not include Reynolds stress profiles in the present paper (since the focus is scaling of the compliant wall response and impact of the critical layer on the deformation–turbulence interactions), the elevations of peak
${y_m}^+\sim 2\sqrt {\delta ^+}$. While we do not include Reynolds stress profiles in the present paper (since the focus is scaling of the compliant wall response and impact of the critical layer on the deformation–turbulence interactions), the elevations of peak ![]() $\langle -u'v'\rangle$ are
$\langle -u'v'\rangle$ are ![]() ${y_m}^+/\sqrt {\delta ^+}=2.00$, 2.03 and 2.04 at
${y_m}^+/\sqrt {\delta ^+}=2.00$, 2.03 and 2.04 at ![]() $Re_\tau =3300$, 6700 and 8900, respectively, i.e. they are very close to the smooth wall values. Furthermore, for two of the present cases,
$Re_\tau =3300$, 6700 and 8900, respectively, i.e. they are very close to the smooth wall values. Furthermore, for two of the present cases, ![]() $Re_{\tau}=6700$ and
$Re_{\tau}=6700$ and ![]() $8900$, the critical layer height is also located at the same elevation. However, at
$8900$, the critical layer height is also located at the same elevation. However, at ![]() $Re_{\tau}=3300$,
$Re_{\tau}=3300$, ![]() ${y_{c}}^{+}=1.1 \sqrt{(\delta^{+})}$, i.e. well below
${y_{c}}^{+}=1.1 \sqrt{(\delta^{+})}$, i.e. well below ![]() ${y_m}^+$. Similarly,
${y_m}^+$. Similarly, ![]() ${y_c}^+$ is lower than
${y_c}^+$ is lower than ![]() ${y_m}^+$ for channel flow data presented in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017), and in the boundary layer results of Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022), with the latter being inferred from the velocity profile and surface wave speed. Hence,
${y_m}^+$ for channel flow data presented in Zhang et al. (Reference Zhang, Wang, Blake and Katz2017), and in the boundary layer results of Greidanus et al. (Reference Greidanus, Delfos, Picken and Westerweel2022), with the latter being inferred from the velocity profile and surface wave speed. Hence, ![]() ${y_c}^+$ is not necessarily associated with the peak in Reynolds stress.
${y_c}^+$ is not necessarily associated with the peak in Reynolds stress.
4. Conclusions
Simultaneous measurements of the 3-D flow, pressure field, and wall deformation in a compliant wall boundary layer enable characterization of the coupling between the flow and surface motion. Conditional analysis reveals that the deformations are highly correlated with pressure fluctuations in the lower part of the log layer. The preferred wave speed of the deformation for all ![]() $Re_\tau$, 0.53
$Re_\tau$, 0.53![]() $U_0$, falls within those of the previous reports that do not show clear trends with material properties or other parameters, a topic requiring further investigation. Combining data obtained from several references, trends of the deformation r.m.s. scaled by the compliant wall thickness collapse when plotted vs pressure fluctuations scaled by the compliant material shear modulus. The nearly linear relationship indicates that the longitudinal strain r.m.s. is proportional to the r.m.s. pressure scaled by the shear (or storage) modulus. To elucidate the impact of deformation wave on the flow field, we adopt the concept of a critical layer that has been developed for characterizing atmospheric wind–wave interactions. In the present data, the critical layer is located within the log layer, increasing in elevation with increasing Reynolds number. The pressure–deformation correlations peak, with magnitudes as high as 0.8, at or slightly above the critical layer. This observation is consistent with Lighthill's (Reference Lighthill1962) claim that most of the energy exchange between the flow and the wave occurs at the critical layer. At lower elevation, the turbulence is phase locked and travels with the surface wave even for deformation amplitudes much smaller than a wall unit. Above this layer, the turbulence is advected at the local mean streamwise velocity, and its correlation with the deformation decays rapidly. Hence, width of the zone with primary wall-turbulence interactions is predominantly prescribed by the surface wave speed. While the deformation height affects the magnitude of energy exchange with the flow, it only impacts the critical layer height through changes to the mean velocity profile.
$U_0$, falls within those of the previous reports that do not show clear trends with material properties or other parameters, a topic requiring further investigation. Combining data obtained from several references, trends of the deformation r.m.s. scaled by the compliant wall thickness collapse when plotted vs pressure fluctuations scaled by the compliant material shear modulus. The nearly linear relationship indicates that the longitudinal strain r.m.s. is proportional to the r.m.s. pressure scaled by the shear (or storage) modulus. To elucidate the impact of deformation wave on the flow field, we adopt the concept of a critical layer that has been developed for characterizing atmospheric wind–wave interactions. In the present data, the critical layer is located within the log layer, increasing in elevation with increasing Reynolds number. The pressure–deformation correlations peak, with magnitudes as high as 0.8, at or slightly above the critical layer. This observation is consistent with Lighthill's (Reference Lighthill1962) claim that most of the energy exchange between the flow and the wave occurs at the critical layer. At lower elevation, the turbulence is phase locked and travels with the surface wave even for deformation amplitudes much smaller than a wall unit. Above this layer, the turbulence is advected at the local mean streamwise velocity, and its correlation with the deformation decays rapidly. Hence, width of the zone with primary wall-turbulence interactions is predominantly prescribed by the surface wave speed. While the deformation height affects the magnitude of energy exchange with the flow, it only impacts the critical layer height through changes to the mean velocity profile.
Supplementary material and movies
Supplementary material and movies are available at https://doi.org/10.1017/jfm.2024.11.
Acknowledgements
The authors would like to dedicate this work to the late Y. Ronzhes, who designed the water tunnel.
Funding
This study is funded by the Office of Naval Research under grant numbers N00014-19-1-2096, N00014-23-1-2681 and N00014-20-1-2778. G. Orris is the program officer.
Declaration of interests
The authors report no conflict of interest.