On the reduction of flow rate losses using thermal waves

Abstract

Flow resistance reduction, quantified as a change in flow rate with respect to a reference isothermal flow driven by the same pressure gradient, is realizable in a channel flow using a thermal wave applied on the bounding wall. Countercurrent waves provide a resistance-reducing effect at any wave velocity, Reynolds number and wavenumber considered. Cocurrent waves can reduce resistance only if the wave velocity is lower than a certain threshold, and the Reynolds number is larger than a certain threshold, otherwise, such waves increase resistance. The increase of the wave amplitude increases resistance reduction and resistance increase up to a specific limit. It is possible to reduce resistance up to 20 times compared with the isothermal channel using proper waves. It is shown that the same effect is achieved regardless of the waves applied at the upper and lower walls. The wave-modified flows are shown to be stable for the conditions used in this study.

1. Introduction

Bounding surfaces in a fluid flow create frictional resistance, leading to energy expenditure required to maintain the flow. This resistance causes an increase in pressure gradient when a fixed mass flow rate is desired and a reduction of the flow rate when a fixed pressure gradient is available. In general, friction occurs due to fluid viscosity, and its magnitude is proportional to the wall-normal velocity gradient. The only possibility for resistance reduction for a given fluid is altering the fluid flow character near the wall. Several techniques have been developed to induce near-wall flow modifications. Examples of passive means include proper surface topography and replacing liquid–solid contact with a liquid–gas interface. An active means introduces a physical quantity, such as piezoelectric actuators (Fukunishi & Ebina 2001), sound (Kato, Fukunishi & Kobayashi 1997), plasma (Inasawa, Ninomiya & Asai 2013), surface transpiration (Bewley & Alamo 2004; Min et al. 2006; Bewley 2009; Hoepffner & Fukagata 2009; Mamori, Iwamoto & Marata 2014; Jiao & Floryan 2021a,b) and surface vibrations (Floryan & Haq 2022; Floryan & Zandi 2022; Haq & Floryan 2022; Floryan & Haq 2023). While none of the methods produced net energy savings, recent results showed that a combination of different techniques might achieve that (Floryan 2023). Active systems may not be suitable for specific applications like the flow of delicate constituents, e.g. bacteria and DNA samples, which are prone to contamination and mechanical breakage.

One can reduce frictional losses by replacing liquid–solid contact with liquid–gas contact by placing micropores on the surface and then filling the pores with gas-forming bubbles (Ou, Perot & Rothstein 2004; Ou & Rothstein 2005; Rothstein 2010; Park, Park & Kim 2013; Srinivasan et al. 2013; Park, Sun & Kim 2014). The shear acting at the solid surface is replaced by shear at the gas interface, which is much lower due to lower gas viscosity. This technique requires two phases and works only with the liquid phase as the main working fluid. An alternate version of this technique considers the liquid infusion into the pores to avoid a potential gas bubble collapse (Solomon, Khalil & Varanasi 2014, 2016; Rosenberg et al. 2016). Although substantial drag reduction has been reported recently (Van Buren & Smits 2017), the effectiveness of this technique diminishes when migration of the infusing liquid occurs due to the variations of pressure along the surface.

One can create special surface topography, such as riblets (short wavelength longitudinal grooves), which can reduce drag by forcing the flow stream to lift above the grooves (Walsh 1983; Garcia-Mayoral & Jimenez 2011). Long-wavelength longitudinal grooves can also contribute to a reduction of the solid–fluid interface friction through changes in the distribution of the bulk flow and are effective on both laminar (Szumbarski, Blonski & Kowalewshi 2011; Mohammadi & Floryan 2013; Moradi & Floryan 2013; Raayai-Ardakani & McKinley 2017; Yadav, Gepner & Szumbarski 2018) and turbulent (Chen et al. 2016; DeGroot, Wang & Floryan 2016) flows. Grooves increase the wetted area compared with a smooth surface; thus, the reduction of the wall shear must be large enough to overcome the increase of the shear caused by the increased area.

In addition to the above techniques, one can consider applying spatially distributed heating patterns on the bounding surface. This heating provides a horizontal density gradient, which creates rotary convection rolls. These rolls prevent direct contact between the stream and the bounding surfaces, reducing the shear experienced by the stream. The effectiveness of this method is increased by adding a uniform heating (Floryan & Floryan 2015), and heating both walls with a proper phase difference between both heating patterns (Hossain & Floryan 2016). The method remains effective for low Reynolds numbers (Hossain, Floryan & Floryan 2012) as stronger flows eliminate the convection bubbles. Drag reduction can be enhanced by properly combining the heating and groove patterns (Hossain & Floryan 2020) by activating the thermal streaming mechanism (Abtahi & Floryan 2017; Floryan, Panday & Aman 2023a). These mechanisms have been confirmed experimentally (Inasawa, Taneda & Floryan 2019; Floryan & Inasawa 2021; Inasawa, Hara & Floryan 2021). The same concept works in vertical and inclined channels (Floryan et al. 2022; Floryan, Wang & Bassom 2023b).

It was demonstrated recently (Hossain & Floryan 2023) that thermal waves propagating along the fluid–solid boundary produce a propulsive effect, generating a net horizontal flow. The waves are characterized by a wave speed, a wavelength, an amplitude and a wave shape. The use of thermal waves, so far, was limited to generating fluid motion (Davey 1967; Hinch & Schubert 1971; Mao, Oron & Alexeev 2013; Reiter et al. 2021). These analyses used the long-wavelength approximation (Davey 1967; Hinch & Schubert 1971), considered slow to moderate wave velocities and high Rayleigh number (Reiter et al. 2021). Mao et al. (2013) considered waves activating the thermocapillary effect rather than the buoyancy effect, with analysis limited to long waves. The question posed in this study is whether thermal waves can reduce resistance in an externally driven flow. Such waves can create convection rolls near the bounding surface (Hossain & Floryan 2023), which were essential for resistance reduction in channels exposed to pattern heating. Thermal waves can be viewed as generating spatially distributed propulsion instead of concentrated propulsion, which could be advantageous in some applications such as where excess local stresses are detrimental to the surface. Reduction of frictional losses is quantified in terms of the flow rate change compared with the flow rate in an isothermal channel driven by the same pressure gradient. We examine the linear stability of the flow to ascertain that no instability occurs under the conditions used in this study, as formation of secondary states would invalidate our predictions. The paper is organized as follows. Section 2 introduces the model problem, and § 3 discusses its numerical solution. Section 4 presents and discusses the solution of the linear stability problem. Section 5 discusses the flow properties starting with § 5.1, describing waves’ pumping effect, and continuing with § 5.2, presenting wave-induced flow modification. The mechanisms governing the flow responses are discussed in § 6, with § 6.1 providing details of flow modifications caused by small amplitude waves, § 6.2 presenting modifications of weak flows, § 6.3 devoted to discussion of long waves and § 6.4 focusing on short waves. Section 7 discusses the results of linear stability analysis, § 8 shows the equivalence between flow response to waves applied at the upper and lower walls and, finally, § 9 provides a summary of the conclusions.

2. Problem formulation

Consider the two-dimensional flow of a fluid confined in a channel bounded by two parallel walls placed at a distance of $2h$ apart from each other, as shown in figure 1. A pressure gradient in the positive $X$-direction drives the flow and the resulting velocity, pressure and flow rate have the form

(2.1a–c)\begin{equation} \boldsymbol{u_0}(X,Y) = [u_0(Y),0] = [1-Y^2,0], \quad p_0(X,Y)={-}2X/Re, \quad Q_0 =4/3, \end{equation}

where $\boldsymbol {u_0} =(u_0,v_0)$ is the velocity vector scaled with the maximum $X$-velocity $u _{max}$ as the velocity scale, $p_0$ denotes the pressure scaled with $\rho u_{max} ^2$ as the pressure scale with $\rho$ being the density of the fluid, $Q_0$ denotes the flow rate, and the Reynolds number is defined as $Re=u_{max} h/\nu$ where $\nu$ stands for the kinematic viscosity and $h$ is the length scale.

Figure 1. Sketch of the flow configuration.

The flow is modified by imposing a thermal wave in the lower wall while the upper wall is kept isothermal. The wave travelling in the positive $X$-direction with the phase speed $c$ and wavenumber $\alpha$ with a known wave profile results in the wall temperatures in the form

(2.2a,b)\begin{equation} \theta_L (t,X) = \tfrac{1}{2} Ra_{P,L} \cos [\alpha (X-ct)], \quad \theta_U (t,X) =0, \end{equation}

where $\theta = (T-T_R)/T_\kappa$ denotes the relative temperature scaled with the temperature scale $T_\kappa = \kappa \nu /(g \gamma h ^{3})$ where $\kappa$ is the thermal diffusivity, $g$ is the gravitational acceleration acting in the negative $Y$-direction, $\gamma$ is the thermal expansion coefficient, $T$ is the absolute temperature and $T_{R}$ is the reference temperature denoting the upper wall temperature. In the above, $t$ denotes time, and the subscripts $L$ and $U$ refer to the lower and the upper wall, respectively. Here $Ra_{P,L}=g \gamma h^{3} \theta _{P,L}/(\kappa \nu )$ is the wave Rayleigh number with $\theta _{P,L}$ is the wave amplitude. The wavelength of the thermal wave $\lambda = 2{\rm \pi} /\alpha$.

Introduction of the thermal wave modifies the flow fields (2.1a–c), which can be represented as a superposition of the pressure-gradient-driven and the buoyancy-driven motions. The complete flow quantities have the form

(2.3)\begin{equation} \left.\begin{gathered} u_1(X,Y) = Re ~ u_0(Y) + u(X,Y), \quad v_1=v(X,Y),\\ \theta_1 = \theta(X,Y), \quad p_1(X,Y)=Re^2\,p_0(X,Y)+p(X,Y), \end{gathered}\right\} \end{equation}

where $(u_1,v_1)$ represent the complete velocity vector with $(X,Y)$ components, $p_1$ and $\theta _1$ denote the complete pressure and temperature fields, respectively. Here $(u, v)$ represent the modification velocity vector with components in the $(X,Y)$ directions, $p$ and $\theta$ denote the pressure and temperature modifications, respectively. The complete velocity vector and the velocity modifications have been scaled using the convective velocity scale $u_{\nu } = \nu /h$ where $u_{max}/u_{\nu } = Re$, the complete pressure and the pressure modifications have been scaled using the pressure scale $\rho u_{\nu }^2$.

Considering the Boussinesq approximation, the resulting two-dimensional flow is described by the unsteady Navier–Stokes, energy and continuity equations of the form

(2.4a)$$\begin{gather} \frac{\partial u }{\partial t} + (Re u_0+u) \frac{\partial u }{\partial X} + Re v \frac{\partial u_0 }{\partial Y}+ v \frac{\partial u }{\partial Y} ={-}\frac{\partial p }{\partial X} + \nabla^2 u, \end{gather}$$

(2.4b)$$\begin{gather}\frac{\partial v }{\partial t} + (Re u_0+u) \frac{\partial v}{\partial X} + v \frac{\partial v }{\partial Y} ={-}\frac{\partial p }{\partial Y} + \nabla^2 v + Pr ^{{-}1} \theta , \end{gather}$$

(2.4c)$$\begin{gather}\frac{\partial \theta }{\partial t} + (Re u_0+u) \frac{\partial \theta }{\partial X} + v \frac{\partial \theta }{\partial Y} = Pr ^{{-}1} \nabla ^2 \theta , \end{gather}$$

(2.4d)$$\begin{gather}\frac{\partial u }{\partial X} + \frac{\partial v }{\partial Y} = 0, \end{gather}$$

where $\nabla ^2$ denotes the Laplace operator and $Pr = \nu /\kappa$ is the Prandtl number. The relevant boundary conditions at the walls are

(2.5a,b)$$\begin{gather} u(t,X, -1)=u(t,X, 1)=0, \quad v(t,X, -1)=v(t,X, 1)=0, \end{gather}$$

(2.5c,d)$$\begin{gather}\theta(t,X, -1)=\theta_L, \quad \theta(t,X, 1)=0. \end{gather}$$

Conditions required for the use of this approximation are discussed in Tritton (1977). Results of experiments for thermal conditions similar to those used in this analysis (Inasawa et al. 2019, 2021; Floryan & Inasawa 2021) demonstrate that the Boussinesq approximation well captures the fluid response.

This analysis intends to determine the effectiveness of thermal waves in reducing flow losses and to quantify their effectiveness. The problem is posed as the determination of change in the flow rate driven through the heated and isothermal channels by the same pressure gradient. This requires imposition of the pressure gradient constraint of the form

(2.6)\begin{equation} \left.\frac{\partial p}{\partial X} \right|_{m}= 0, \end{equation}

where the subscript $m$ denotes the mean value.

The total mean flow rate in the channel is decomposed into two parts: the reference isothermal flow rate and the flow rate correction $Q_c$ induced by the wave, i.e.

(2.7a,b)\begin{equation} \left.Q_T(t,X) \right|_{m}= \tfrac{4}{3}Re +\left. Q_c(t,X) \right|_{m}, \quad \left.Q_c (t,X) \right|_{m} = \left[ \int_{{-}1} ^{1} u(t,X,Y) \,{\rm d}Y \right]_{m}. \end{equation}

Positive values of the correction $Q_c$ identify conditions leading to resistance reduction. The flow rate increase (decrease) is better illustrated using the correction factor $\varGamma _{cor}$ defined as

(2.8)\begin{equation} \varGamma_{cor} = \frac{Q_c}{\dfrac {4}{3}Re}, \end{equation}

which expresses the flow rate correction as a fraction of the reference flow rate.

Determination of surface forces acting on the fluid contributes to the understanding of the flow mechanics. The wall shear stress at the lower wall ($\sigma _{X,L}$) can be calculated as

(2.9a)\begin{equation} \sigma_{X,L} = \left.-\frac{\partial u}{\partial Y} \right|_{Y={-}1} - 2Re = \sigma_{X,L,mod} -2Re, \end{equation}

where $\sigma _{X,L,mod}$ is the shear stress modification due to interaction of the thermal wave, and the corresponding $X$-component of the shear force modification $(\tau _{X,L,mod})$ per its unit length can easily be determined as

(2.9b)\begin{equation} \tau_{X,L,mod} ={-} \lambda ^{{-}1} \int_{X_0} ^{X_0 + \lambda} \left.\left( \frac{\partial u}{\partial Y} \right) \right|_{Y={-}1} \,{\rm d}X, \end{equation}

where $X_0$ is a convenient reference point. Similar quantities, i.e. $\sigma _{X,U}$ and $\tau _{X,U,mod}$, can be defined for the upper wall.

3. Method of solution

Introduction of a frame of reference moving with the wave phase speed and use of the relevant Galileo transformation of the form $y=Y, x=X-ct$ leads to a steady problem of the form

(3.1a)$$\begin{gather} (Re u_0+u-c) \frac{\partial u }{\partial x} + Re v \frac{\partial u_0 }{\partial y}+ v \frac{\partial u }{\partial y} ={-}\frac{\partial p }{\partial x} + \frac{\partial^2 u }{\partial x^2} +\frac{\partial^2 u }{\partial y^2}, \end{gather}$$

(3.1b)$$\begin{gather}(Re u_0+u-c) \frac{\partial v}{\partial x} + v \frac{\partial v }{\partial y} ={-}\frac{\partial p }{\partial y} + \frac{\partial^2 v }{\partial x^2} +\frac{\partial^2 v }{\partial y^2} + Pr ^{{-}1} \theta , \end{gather}$$

(3.1c)$$\begin{gather}(Re u_0+u-c) \frac{\partial \theta }{\partial x} + v \frac{\partial \theta }{\partial y} = Pr ^{{-}1} \left[ \frac{\partial^2 \theta }{\partial x^2} +\frac{\partial^2 \theta }{\partial y^2} \right], \end{gather}$$

(3.1d)$$\begin{gather}\frac{\partial u }{\partial x} + \frac{\partial v }{\partial y} = 0, \end{gather}$$

with the boundary conditions taking the following form:

(3.1e–h)\begin{equation} \left.\begin{gathered} u(y=\pm1)=v(y=\pm1)=0, \quad \theta(y={-}1)=\theta_L (x) = \frac{1}{2} Ra_{p,L} \cos(\alpha x),\\ \theta(y=1)= \theta_U (x) =0, \quad \left.\frac{\partial p}{\partial x} \right|_{m}= 0. \end{gathered}\right\} \end{equation}

Introduction of stream function $\psi$ defined as $u=\partial \psi / \partial y$, $v=-\partial \psi /\partial x$, and elimination of pressure provide the following form of the field equations:

(3.2a)\begin{align} \nabla ^4 \psi + c \frac{\partial }{\partial x} (\nabla ^2 \psi) - Pr ^{{-}1} \frac{\partial \theta }{\partial x} &= Re\,u_0\frac{\partial }{\partial x} (\nabla ^2 \psi) -Re\,\frac{{\rm d}^2 u_0 }{{{\rm d}y}^2} \frac{\partial \psi }{\partial x}+ \frac{\partial \psi }{\partial y} \frac{\partial }{\partial x}(\nabla ^2 \psi) \nonumber\\ &\quad -\frac{\partial \psi }{\partial x} \frac{\partial }{\partial y}(\nabla ^2 \psi), \end{align}

(3.2b)\begin{align} \nabla ^2 \theta +c Pr \frac{\partial \theta}{\partial x} &= Re Pr u_0\frac{\partial \theta }{\partial x}+ Pr \left( \frac{\partial \psi }{\partial y} \frac{\partial \theta }{\partial x} -\frac{\partial \psi }{\partial x} \frac{\partial \theta }{\partial y} \right), \end{align}

subject to

(3.2c–f)\begin{align} \frac{\partial \psi}{\partial y} ({\pm} 1)=\frac{\partial \psi}{\partial x} ({\pm} 1)=0, \quad \theta ({-}1) = \frac{1}{2} Ra_{p,L} \cos(\alpha x), \quad \theta (1) =0, \quad \left.\frac{\partial p}{\partial x} \right|_{m}= 0, \end{align}

where $\nabla ^4$ stands for the biharmonic operator.

The system of (3.2a–f) is solved by representing the unknowns in terms of Fourier expansions in the streamwise direction as

(3.3a,b)\begin{equation} \psi (x,y) = \sum_{n={-}\infty} ^{n={+}\infty} \psi ^{(n)} (y) {\rm e}^{{\rm i}n\alpha x }, \quad \theta (x,y) = \sum_{n={-}\infty} ^{n={+}\infty} \theta ^{(n)} (y) {\rm e}^{{\rm i}n\alpha x } \end{equation}

where the modal functions $\psi ^{(n)} (y)$ and $\theta ^{(n)} (y)$ are to be determined. The pressure gradient constraint (3.2f) can be expressed in terms of modal functions as

(3.4)\begin{equation} \frac{{\rm d}^2 \psi }{{{\rm d}y}^2} ^{(0)} (1) - \frac{{\rm d}^2 \psi }{{{\rm d}y}^2} ^{(0)} ({-}1)= 0. \end{equation}

For the purpose of numerical solution, expansions (3.3a,b) are truncated after a finite number of terms $N_M$ resulting in a system of $2(N_M+1)$ equations which are solved using a Chebyshev collocation technique based on $N_P$ collocation points (Canuto et al. 1996). An under-relaxation-based iterative technique is used to control solution accuracy within the specified tolerance limit. The number of collocation points and the Fourier modes used in the solution have been selected through numerical experiments to guarantee at least six digits accuracy.

Using the Fourier modal functions, the flow rate correction is simply evaluated as

(3.5)\begin{equation} \left.Q_c(x)\right|_{m} = \psi ^{(0)} (1), \end{equation}

and the expressions for the shear force modifications reduce to much simpler form as

(3.6a,b)\begin{equation} \tau_{x,L,mod} =\left. -D^2 \psi ^{(0)} \right|_{y={-}1}, \quad \tau_{x,U,mod} = \left.D^2 \psi ^{(0)} \right|_{y=1}. \end{equation}

4. Linear stability analysis

In order to have a reliable prediction of the flow rate, we determine whether the flow discussed above undergoes any bifurcations which, if they occur, would invalidate predictions.

We shall use linear stability theory in order to determine the onset conditions (Floryan 1997; Hossain & Floryan 2013). The analysis begins with the three-dimensional forms of the momentum, energy and continuity equations expressed in the moving frame of reference, shown in (3.1). We superimpose unsteady, three-dimensional infinitesimal disturbances into the wave-modified flow and represent the flow field as

(4.1a–c)\begin{gather} \boldsymbol{v} = \boldsymbol{v_1} (x,y) + \boldsymbol{v_2} (x,y,z,t),\quad \theta = \theta_1 (x,y) + \theta_2 (x,y,z,t), \quad p = p_1 (x,y) + p_2 (x,y,z,t). \end{gather}

In the above, the subscripts 1 and 2 refer to the wave-modified flow and the disturbance fields, respectively, with $\boldsymbol {v_1}=(u_1,v_1,0)$ standing for the modified flow velocity vector, $\boldsymbol {v_2}=(u_2,v_2,w_2)$ standing for the disturbance velocity vector, $\theta _1$ denoting the modified temperature, $\theta _2$ denoting the temperature disturbance, $p_1$ standing for the modified pressure field and $p_2$ standing for the disturbance pressure field. Substitution of the flow quantities (4.1) into the field equations, subtraction of the wave-modified part (3.1) and linearization of the resulting equations provide the following disturbance equations in vector form:

(4.2a)$$\begin{gather} \frac {\partial \boldsymbol{v}_2}{\partial t} +Re u_0\frac{\partial \boldsymbol{v}_2}{\partial x}-c\frac{\partial \boldsymbol{v}_2}{\partial x} + (\boldsymbol{v_2} \boldsymbol{\cdot}\boldsymbol{\nabla})\boldsymbol{v}_1 + (\boldsymbol{v_1} \boldsymbol{\cdot}\boldsymbol{\nabla})\boldsymbol{v}_2 ={-} \boldsymbol{\nabla}p_2 + \nabla^2 \boldsymbol{v}_2 + Pr^{{-}1} \theta_2 \kern 1.5pt\boldsymbol{j}, \end{gather}$$

(4.2b)$$\begin{gather}\frac{\partial \theta_2}{\partial t} +Re u_0\frac{\partial \theta_2}{\partial x}-c\frac{\partial \theta_2}{\partial x} + (\boldsymbol{v_2} \boldsymbol{\cdot}\boldsymbol{\nabla}) \theta_1 + (\boldsymbol{v_1} \boldsymbol{\cdot}\boldsymbol{\nabla}) \theta_2 = Pr^{{-}1} \nabla ^2 \theta_2, \end{gather}$$

(4.2c)$$\begin{gather}\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{v}_2 = 0, \end{gather}$$

where $\boldsymbol {j}$ is the unit vector along vertical $y$-direction. The above system is subject to the homogeneous boundary conditions

(4.2d,e)\begin{equation} \boldsymbol{v}_2({\pm} 1)=0, \quad \theta_2({\pm} 1)=0. \end{equation}

System (4.2) represents a linear stability system for a thermal-wave spatially modulated flow with its spatial distribution of modulations characterized by the wavenumber $\alpha$. Spatial distribution of disturbances is characterized by the spanwise ($\beta )$ and streamwise ($\delta$) wavenumbers. The overall system periodicity in the spanwise direction is characterized by $\beta$ while the character of this system in the $x$-direction depends on the ratio of $\alpha$ and $\delta$. The system can be aperiodic in this direction for an irrational ratio of $\alpha$ and $\delta$ (non-commensurate system), and could be periodic but with wavelengths varying by several orders of magnitude (commensurate systems). Wavenumber $\alpha$ can be viewed as a control parameter as its value characterizes the thermal wave of interest. The stability analysis requires determination of the amplification rate for $\beta \in (0,\infty )$ and $\delta \in (0,\infty )$ which, in the case of direct-numerical-simulation-type solutions, necessitates use of very large solution domains which makes such solutions impractical, if not impossible (Panday & Floryan 2023). Here we follow the formulation proposed by Floryan (1997).

The disturbance quantities are represented as

(4.3a)\begin{equation} \left [ \boldsymbol{v_2}, \theta_2, p_2 \right ](x,y,z,t) = \left [ \boldsymbol{V_2}, \varTheta_2, P_2 \right ] (x,y) \exp({{\rm i} (\delta x + \beta z -\sigma t)}) + {\rm c.c.}, \end{equation}

where ($\delta, \beta$) are the disturbance wavenumber in the ($x, z$) directions, the real and imaginary parts of the complex exponent $\sigma = \sigma _r + \textrm {i} \sigma _i$ describe the rate of growth and the frequency of disturbances with positive $\sigma _i$ identifying instability and c.c. stands for the complex conjugate. Here $\boldsymbol {V_2} (x,y)$, $\varTheta _2 (x,y)$, and $P_2(x,y)$ are the $x$-periodic amplitudes functions. Substitution of (4.3a) into (4.2) leads to an eigenvalue problem for the partial differential equations for the amplitude functions. These functions are represented as Fourier expansions in the $x$-direction

(4.3b)\begin{equation} \left [ \boldsymbol{V_2}, \varTheta_2, P_2 \right ] (x,y) = \sum_{m={-}\infty} ^{m={+}\infty} \left [ \left ( f_u ^{(m)},f_v ^{(m)}, f_w ^{(m)} \right), f_\theta ^{(m)}, f_p^{(m)} \right ] (y) {\rm e} ^{{\rm i} m \alpha x }. \end{equation}

We transform the system (4.2a,b) into wall-normal vorticity $(\zeta = {\partial u_2}/{\partial z} - {\partial w_2}/{\partial x})$ and wall-normal velocity ($v$) form, substitute (4.3a,b) and separate the Fourier components, after some rather lengthy algebra, to arrive at a system of linear homogeneous ordinary differential equations of the form

(4.4a)$$\begin{gather} A^{(m)} \zeta ^{(m)} +Re D u_0 \beta f_v^{(m)} = \sum_{n={-}\infty} ^{n={+}\infty} [ H_\zeta ^{(m-n)} \zeta ^{(m-n)}+H_v ^{(m-n)} f_v ^{(m-n)}], \end{gather}$$

(4.4b)$$\begin{gather}B^{(m)} f_v ^{(m)} - Pr ^{{-}1} k_m ^2 \,f_\theta^{(m)} ={-}\sum_{n={-}\infty} ^{n={+}\infty} [ L_\zeta ^{(m-n)} \zeta ^{(m-n)}+L_v ^{(m-n)} f_v ^{(m-n)}], \end{gather}$$

(4.4c)$$\begin{gather}C^{(m)} f_\theta^{(m)} = Pr \sum_{n={-}\infty} ^{n={+}\infty} [ J_\zeta ^{(m-n)} \zeta ^{(m-n)}+J_v ^{(m-n)} f_v ^{(m-n)} +J_\theta ^{(m-n)} f_\theta ^{(m-n)}] , \end{gather}$$

and the boundary conditions take the form

(4.4d–g) \begin{equation} \left.\begin{gathered}\zeta ^{(m)}({\pm} 1)=0, \quad f_v ^{(m)}({\pm} 1)=0, \quad D f_v ^{(m)}({\pm} 1)=0, \\ f_\theta ^{(m)}({\pm} 1)=0\quad {\rm for}\ {-}\infty < m<{+}\infty,\end{gathered} \right\} \end{equation}

with the coefficients $A, B, C, H, L, J$ being given in Appendix A.

The linear disturbance equations (4.4) represent an eigenvalue problem and are discretized with spectral accuracy using the Chebyshev collocation method with $N_P$ collocation points (Canuto et al. 1996) and truncating after $N_M$ modes. For the purposes of calculations, the problem is posed as an eigenvalue problem for $\sigma$. The resulting matrix system is solved by the ‘inverse iteration’ technique as described in Saad (2011).

5. Flow characteristics

It is convenient to start with a short outline of the reference case of $Re=0$, which has been studied previously by Hossain & Floryan (2023).

5.1. Thermal waves’ pumping effect

When there is no flow in the channel, a thermal wave acting on the lower wall can pump fluid horizontally at a rate $Q$ in the direction opposite to wave propagation. The flow response for a wave travelling to the right is a mirror image of the response for a wave travelling to the left; $Q$ is positive for the leftward wave, whereas it is negative for the rightward wave. Figure 2(a) shows that an increase in wave velocity $|c|$ increases $|Q|$ at the rate proportional to ${\sim }|c|$, but after reaching a maximum, its further increase reduces $|Q|$ proportionally to ${\sim }|c|^{-4}$. Figure 2(b) demonstrates that an excessive increase in the wave wavelength reduces $|Q|$ proportionally to $\sim \alpha ^4$, whereas an excessive reduction reduces $|Q|$ proportionally to $\sim \alpha ^{-6}$. The largest $|Q|$ occurs for waves with the wavenumbers $\alpha \in [1,4]$ and phase speed $|c| \in [1,5]$. An increase in the wave amplitude $Ra_{p,L}$ increases the flow rate proportionally to $\sim Ra_{p,L} ^2$, as shown in figure 2(c), but an excessively large amplitude slows down the increase due to various saturation effects. The pumping effect is known to be associated with the propulsion provided by the convection rollers (see figure 3) formed due to wave diffusion into the channel interior. At large $|c|$ and $\alpha$, these rollers appear very near to the lower wall, forming a boundary layer and reducing $|Q|$ drastically.

Figure 2. (a) Variation of the flow rate correction $Q_c$ as a function of the wave speed $c$, (b) wave wavenumber $\alpha$ and (c) wave amplitude $Ra_{p.L}$ for $Re =0$, $Pr=0.71$. Asymptotes are depicted by dashed lines. In (a,c) $\alpha =2$, and in (b) $Ra_{p.L}=1000$.

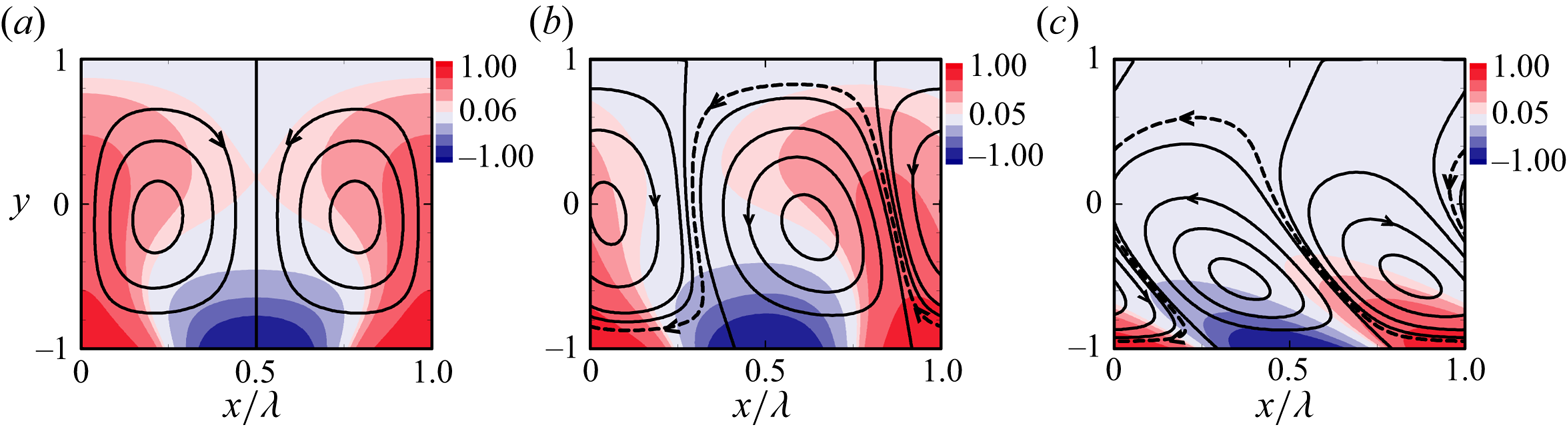
Figure 3. Flow topology (line) and temperature (filled colour) field at $Re =0$ with (a) $c=0$, (b) $c=2$ and (c) $c=20$ for $Ra_{p,L}=1000$, $\alpha =2$, $Pr=0.71$. The dashed lines show the meandering flow stream. Arrows show the stream flow direction.

Variations of flow topology associated with variation of $c$ are illustrated in figure 3. As the waves diffuse into the channel interior, they are delayed by the fluid thermal inertia, with their positions falling farther behind the surface waves as the distance from the lower wall increases. This process results in bubbles tilting. We refer to this effect as the lagging thermal penetration. The bubble tilting occurs leftward when the wave travels rightward ($c> 0$), and rightward when the wave travels leftward ($c < 0$).

5.2. Flow modifications generated by thermal waves

There is an established isothermal flow from left to right characterized by $Re$. This flow is modified by a thermal wave with wave velocity $c$ applied at the lower wall. Its response depends on $Re$ and $c$. A stationary wave ($c=0$) represents the reference configuration with flow topology displayed in figure 4. The topology for $Re=0$ consists of pairs of counter-rotating rolls and has vertical mushroom-shaped isotherms (figure 4a). Introduction of a weak flow, e.g. $Re=1$, causes these rolls to separate, creating a narrow meandering stream between them (figure 4b). The rolls morph into upper and lower wall separation bubbles, with the upper bubbles rotating anticlockwise and the lower bubbles rotating clockwise. The bubbles and isotherms are slightly tilted rightward. Further, an increase in $Re$ eliminates the upper bubbles (figure 4c), reduces the size of the lower bubbles and increases the rightward tilt of the bubbles and isotherms. A fast enough flow (e.g. $Re>20$) washes away even the lower bubbles, bringing the flow to a parallel form (figure 4d), with the titled isotherms concentrated only near the lower wall. The flow advects a portion of the applied wall heat horizontally, and the rest diffuses into the interior of the channel. We refer to this as leading thermal penetration, resulting in the bubbles and isotherms tilting along the flow direction.

Figure 4. Flow topology (line) and temperature (filled colour) field at $c=0$ with (a) $Re=0$, (b) $Re=1$, (c) $Re=10$, (d) $Re=20$ for $Ra_{p,L}=1000$, $\alpha =2$, $Pr=0.71$. The grey dashed lines show the meandering flow stream. Arrows show the stream flow direction.

Response to the moving wave is illustrated in figure 5 for $Re=1$ flow. The flow topology remains qualitatively similar for larger $Re$ (not shown), with the bubbles decreasing in size. The use of low-velocity waves ($c=1$) directed along the flow direction results in an appearance of a rightward (i.e. towards flow direction) shift of the position of the bubbles (figure 5a), which is mainly due to the formation of a thicker stream tube carrying fluid to the right. The upper bubbles shift to the left and exhibit right tilting (figure 5b). Further increase of $c$ eventually eliminates the bubbles (figure 5c,d). The tilting is caused by delay associated with heat diffusion into the flow interior (the rightward wave movement is faster than the heat diffusion across the stream), i.e. thermal lagging. Reversing the wave's direction to opposite the flow (see figure 5e–h) has qualitatively similar effects on the bubbles’ sizes and their eventual elimination but causes rightward tilt, which increases with the wave velocity. One can note that thermal lagging causes tilting along flow direction when the wave travels leftward ($c<0$). The rightward wave ($c>0$) produces tilting in the direction opposite to the flow.

Figure 5. Flow topology (line) and temperature (filled colour) field at $Re=1$ with (a) $c=1$, (b) $c=10$, (c) $c=20$, (d) $c=70$, (e) $c=-1$, ( f) $c=-10$, (g) $c=-20$ and (h) $c=-70$ for $Ra_{p,L}=1000$, $\alpha =2$, $Pr=0.71$. The grey dashed lines show the meandering flow stream. Arrows show the stream flow direction.

The effects of $Re$ and $c$ can be gleaned from figure 6, displaying variations of the correction factor $\varGamma _{cor}=Q_c/(\frac {4}{3}Re)$ defined in (2.8), as a function of $Re$ and $c$. Conditions leading to the reduction of flow losses are marked using grey colour. A characteristic, nearly straight line separates the resistance-reducing from the resistance-increasing waves. Conditions along this line identify the critical wave speed $c_n$ and the critical Reynolds number $Re_n$, with $c_n = 0.77 Re_n$, which results in zero flow rate correction $Q_c=0$. The countercurrent waves always reduce flow resistance. Their effectiveness is largest for small $Re$ where they can increase flow rate up to ${\sim }20$ times compared with the reference isothermal flow. The cocurrent waves also reduce resistance, but such waves cannot be too fast as fast enough waves increase resistance. Such waves are less effective than countercurrent waves, providing only up to 20 % flow rate increase. These results demonstrate a potential for significantly reducing flow losses by waves with proper characteristics.

Figure 6. Variation of the correction factor $\varGamma _{cor}$ as a function of Reynolds number $Re$ and wave speed $c$ for $\alpha =2$, $Ra_{p,L} =1000$, $Pr=0.71$. Grey shaded zone identifies conditions leading to flow rate increase with respect to the reference isothermal flow. The thick line illustrates variation of the critical Reynolds number $Re_n$ as a function of the critical wave velocity $c_n$, which can be approximated as $c_n = 0.77 Re_n$. Vertical (purple) and horizontal (blue) dotted lines identify conditions used in figures 9 and 10, respectively.

We shall now discuss how waves affect flow structures. The introduction of waves activate three effects. The first one is the reduction of direct contact between the stream and the bounding walls, which reduces friction experienced by the stream. The second one involves additional propulsion generated by the bubbles’ rotation as the bubbles rotate in the stream direction, which is favourable to the flow. The third one is flow blockage by the bubbles (reduction of flow cross-sectional area), which increases flow losses. As $Re$ increases, bubbles are eventually washed away, eliminating the resistance-reducing effect. The net effect of waves on the flow rate can be determined by integrating the modal function $u^{(0)}$ across the channel. Figure 7 illustrates the distribution of this function for a variety of conditions. A wave with critical velocity $c_n=0.77$ produces modal function $u^{(0)}=0$ across the channel, thus no change in the flow rate. Other waves generally produce large flow rate changes in the upper portion of the channel and relatively smaller changes in the lower portion, so the upper portion determines the overall flow rate correction. Waves with $c< c_n$ (countercurrent waves and sufficiently slow cocurrent waves) produce a large flow rate increase in the upper portion of the channel and the overall flow rate increase, while sufficiently fast cocurrent waves produce large flow rate decrease in the upper portion and the overall flow rate decrease.

Figure 7. Distribution of the modal function $u^{(0)}$ for selected values of $c$ at $Re = 1$, $Ra_{p,L} = 1000$, $\alpha = 2$, $Pr = 0.71$.

Wave action changes wall shear, which may increase or decrease depending on the flow conditions and wave characteristics. Change in the shear is responsible for the change in the flow rate. Distributions of shear modifications for different wave velocities, propagation directions and flow Reynolds numbers are displayed in figures 8(a) and 8(b). The shear distribution is symmetric for waves with velocity $c_n$, producing a zero mean value. Waves with $c \ne c_n$ break this symmetry, producing a net shear force with the modifications equal and opposite in the lower and upper walls. Waves travelling opposite to the flow ($c<0$) and sufficiently slow waves travelling in the flow direction ($c< c_n$) produce positive modification at the lower wall, whereas sufficiently fast waves travelling in the flow direction ($c>c_n$) produce negative modifications. When mean shear at $c=c_n$ is used as a reference point, an increase of $|c-c_n|$ causes the magnitude of the average shear modification to initially increases, attains a maximum and then decrease with a further increase of $|c-c_n|$ (figure 8c). The decrease at large $|c|$ is proportionally to $|c|^{-4}$ (see Appendix B for discussion on the asymptote).

Figure 8. Wall shear force modification $\tau _{mod}$ profiles and mean shear modifications $\tau _{av}$ at the (a) lower and (b) upper wall for selected values of $c$ at $Re = 1$, $Ra_{p,L} = 1000$, $\alpha = 2$, $Pr = 0.71$. Subscripts $L$ and $U$ denote the lower and upper wall, respectively. The dotted line shows shear for $c_n=0.77$. Panel (c) displays the average wall shear force modification at the lower wall and in this figure, solid and dashed lines show positive and negative values, respectively. Large $c$ asymptotes are shown by dotted lines.

Variations of the flow rate correction $Q_c$ as a function of $c$ are illustrated in detail in figure 9 for $Re=1$, 10, 20. The critical wave velocity for each $Re$ is $c_n=0.77$, 7.7, 15.4, respectively; $c< c_n$ provides positive flow rate correction, causing an overall decrease of flow resistance, but $c>c_n$ provides negative flow rate correction, causing the overall increase in flow resistance. When $c$ either increases or decreases away from $c_n$, the flow rate correction exhibits a qualitatively similar response – its magnitude initially increases, attains a maximum and then gradually decreases, eventually becoming proportionally to $|c|^{-4}$.

Figure 9. Variation of the flow rate correction $Q_c$ as a function of wave speed $c$ for selected values of $Re$. Solid and dashed lines show positive and negative values, respectively. Large $c$ asymptotes are shown by dotted lines. Flow conditions used in this figure are identified by purple dotted lines in figure 6.

Figure 10 illustrates in more detail how an increase of $Re$ affects $Q_c$. The selected curves corresponding to $c=0, \pm 0.1, \pm 2$ and $\pm 10$ illustrate how the flow response changes with the wave direction change and clearly identify the change from an increase of the flow rate to its decrease as $Re$ increases. There are well-defined limits of $Q_c$ for $Re\rightarrow 0$, which are positive for negative $c$ and negative for positive $c$, with $c=0$ representing the boundary between them characterized by $Q_c \rightarrow 0$ with $Re \rightarrow 0$. The case of $Re=0$ corresponds to the pumping problem studied in Hossain & Floryan (2023) and briefly reviewed in § 5.1. It is interesting to note that in the case of $c=0$, $Q_c$ initially increases proportionally to $Re$, attains a maximum and then decreases with the further increase of $Re$ proportionally to $Re ^ {-2.5}$. Countercurrent waves produce $Q_c$ changing marginally with $Re$ until $Re$ becomes large enough to cause a decrease proportional to $Re ^ { -2.5}$. The behaviour of cocurrent waves is qualitatively similar if one considers $|Q_c|$, i.e. there is a well-defined limit for small $Re$ and well-defined behaviour for large $Re$, except in the neighbourhood of $Re=Re_n$ where $Q_c$ passes through zero. A countercurrent wave, a wave travelling opposite the flow ($c < 0$), always provides $Q_c > 0$. The cocurrent wave, a wave travelling along the flow ($c > 0$), increases flow losses if $Re< Re_n$ and decreases flow losses when $Re>Re_n$. One, of course, needs to remember that a flow that is too fast ($Re$ too big) washes away bubbles, and the flow resistance loses any dependence on the thermal waves.

Figure 10. Variation of the flow rate correction $Q_c$ as a function of Reynolds number $Re$ for selected values of $c$. Solid and dashed lines show positive and negative values, respectively. Small and large $Re$ asymptotes are shown by dotted lines. Flow conditions used in this figure are identified by blue dotted lines in figure 6.

Effects of a wave's wavelength are illustrated in figure 11. As the wavenumber increases, the countercurrent waves reduce resistance ($Q_c >0$) proportionally to ${\sim }\alpha ^4$, the resistance reduction attains a maximum and then decreases proportionally to ${\sim }\alpha ^{-6}$ (details of the analysis are given in § 6). Cocurrent waves exhibit a similar trend but with a notable difference. They reduce resistance ($Q_c>0$) if they are sufficiently slow and increase resistance if they are fast enough. An estimate of the critical velocity $c_n$ can be obtained from analytical solutions for large and small $\alpha$, i.e.

(5.1a)$$\begin{gather} c_{n} = \frac{(1929+3130 Pr)Re}{3435(1+Pr)} \quad \alpha \rightarrow 0, \end{gather}$$

(5.1b)$$\begin{gather}c_{n} = \frac{(27+22Pr)Re}{4 \alpha(1+Pr)} \quad \alpha \rightarrow \infty. \end{gather}$$

Figure 11. Variation of the flow rate correction $Q_c$ as a function of wave wavenumber $\alpha$ for selected values of $c$ at $Ra_{p,L}$ =1000, $Re=1$, $Pr=0.71$. Solid and dashed lines show positive and negative, respectively. Large and small $\alpha$ asymptotes are shown by dotted lines.

Variations of $\varGamma _{cor}$ as a function of $c$ and $\alpha$ displayed in figure 12 permit a quick identification of the most effective waves. Waves with $\alpha \approx 2$ and $c \in [-2, -3]$ produce the largest resistance reduction, and waves with $\alpha \approx 2$ and $c \in [3, 5]$ produce the largest resistance increase. The maximum resistance reduction occurs for $\alpha = \alpha _{max} \approx 2$ with $\alpha _{max}$ decreases marginally with $c$. The reader may note that the critical wave velocity $c_n$ varies marginally as a function of $\alpha$.

Figure 12. Variation of the correction factor $\varGamma _{cor}$ as functions of wave wavenumber $\alpha$ and wave speed $c$ for $Re=1$, $Ra_{p,L}=1000$, $Pr=0.71$. Grey shaded zone identifies conditions leading to an increase of the flow rate above the flow rate in the reference isothermal channel.

Results displayed in figure 13 demonstrate that the magnitude of change of resistance initially increases proportionally to ${\sim }Ra_{p,L}^2$ . This growth slows down for $Ra_{p,L}> \sim 2000$ due to saturation effects, which suggests that excessively large heating is not beneficial. Also, the results of stability analysis discussed in § 7 suggest a possible transition to secondary states for excessively large wave amplitudes.

Figure 13. Variation of the flow rate correction $Q_c$ as a function of wave intensity $Ra_{p,L}$ for selected values of $c$ at $\alpha =2$, $Re=1$, $Pr=0.71$. Solid and dashed lines show positive and negative values, respectively. Small $Ra_{p,L}$ asymptote is shown by dotted lines.

One may wish to ascertain the effectiveness of a moving thermal wave over a stationary heating pattern. Figure 14 displays variations of the stationary gain factor $\varGamma _s$, defined as

(5.2)\begin{equation} \varGamma_s = \frac{Q_c-Q_c|_{c=0}}{Q_c|_{c=0}}, \end{equation}

with $Q_c|_{c=0}$ denoting the flow rate correction when $c=0$. Positive values of $\varGamma _s$ correspond to the moving wave being more effective. Variation of the critical wave velocity $c_n=0.77Re$ in figure 14(a,c) corresponds to $\varGamma _s=-1$, with $c_n$ varying marginally with $\alpha$ shown in figure 14(b,d). In general, countercurrent waves are more effective (as high as ${\sim }100$ fold) for small $Re$ while cocurrent waves are more effective for larger $Re$ (figure 14a,c). Use of $\alpha = 4$–$5$ provides the best improvement achieve by the waves (figure 14b,d).

Figure 14. Variation of the stationary gain factor $\varGamma _{s}$ as functions of (a,c) $Re$ and $c$ at $\alpha =2$ (b,d) $\alpha$ and $c$ at $Re=1$, for $Ra_{p,L}=1000$, $Pr=0.71$. Grey shaded zone denotes flow rate increase over the stationary heating pattern. In (a,c), the line $\varGamma _{s}=-1$ represents $c_n = 0.77 Re$. In (b,d), the line $\varGamma _{s}=-1$ represents $c_n$.

In the next section, we analyse the mechanisms driving the flow response.

6. Mechanism governing the flow response

The mechanisms governing flow response are discussed with the help of analytic solutions, which can be obtained in special limits. We start with the small amplitude waves.

6.1. Small amplitude wave

We introduce a small parameter $\epsilon \ll 1$ which measures the wave amplitude. The flow quantities are assumed to be asymptotic power series of $\epsilon$ as

(6.1)\begin{equation} (u,v,\theta,p)=\epsilon (U_1, V_1,\varTheta_1, P_1)+ \epsilon ^2 [U_2, V_2,\varTheta_2, P_2] + O(\epsilon ^3). \end{equation}

Substitution of (6.1) into (3.1) leads to a system of $O(\epsilon )$ in the form

(6.2a)$$\begin{gather} \nabla ^2 U_1 -Re u_0 \frac{\partial U_1 }{\partial x}-Re \frac{{\rm d} u_0 }{{\rm d}y} V_1 +c \frac{\partial U_1 }{\partial x} -\frac{\partial P_1 }{\partial x} =0, \end{gather}$$

(6.2b)$$\begin{gather}\nabla ^2 V_1 -Re u_0 \frac{\partial V_1 }{\partial x} +c \frac{\partial V_1 }{\partial x} -\frac{\partial P_1 }{\partial y} ={-} Pr ^{{-}1} \varTheta_1 , \end{gather}$$

(6.2c)$$\begin{gather}\nabla ^2 \varTheta_1 -RePru_0 \frac{\partial \varTheta_1 }{\partial x} + c Pr \frac{\partial \varTheta_1 }{\partial x} =0 , \end{gather}$$

(6.2d)$$\begin{gather}\frac{\partial U_1 }{\partial x} + \frac{\partial V_1 }{\partial y} = 0, \end{gather}$$

(6.2e–h)\begin{equation} U_1(\pm1)=V_1(\pm1)=0, \quad \varTheta_1 ({-}1) = \tfrac{1}{2} Ra_{p,L} \cos(\alpha x), \quad \varTheta_1 (1) =0, \quad \left. {\partial P_1}/{\partial x} \right|_{m}= 0 \end{equation}

and a system of $O(\epsilon ^2)$ in the form

(6.3a)$$\begin{gather} \nabla ^2 U_2 -Reu_0 \frac{\partial U_2 }{\partial x} -Re \frac{{\rm d} u_0 }{{\rm d}y} V_2 +c \frac{\partial U_2 }{\partial x} -\frac{\partial P_2 }{\partial x} = U_1 \frac{\partial U_1 }{\partial x} + V_1 \frac{\partial U_1 }{\partial y} , \end{gather}$$

(6.3b)$$\begin{gather}\nabla ^2 V_2 -Reu_0 \frac{\partial V_2 }{\partial x} +c \frac{\partial V_2 }{\partial x} -\frac{\partial P_2 }{\partial y} ={-}Pr ^{{-}1} \varTheta_2 + U_1 \frac{\partial V_1 }{\partial x} + V_1 \frac{\partial V_1 }{\partial y} , \end{gather}$$

(6.3c)$$\begin{gather}\nabla ^2 \varTheta_2 -Reu_0 Pr \frac{\partial \varTheta_2 }{\partial x} + c Pr \frac{\partial \varTheta_2 }{\partial x} = Pr U_1 \frac{\partial \varTheta_1 }{\partial x} + Pr V_1 \frac{\partial \varTheta_1 }{\partial y} , \end{gather}$$

(6.3d)$$\begin{gather}\frac{\partial U_2 }{\partial x} + \frac{\partial V_2 }{\partial y} = 0, \end{gather}$$

which is subject to homogeneous boundary conditions and a constraint associated with constant mean-pressure-gradient.

We start with the solution of (6.2c) for the temperature $\varTheta _1$ which is subject to the forcing (6.2f–g) leading to assume a solution in the form

(6.4)\begin{equation} \varTheta_1 (x,y)= \varTheta_1 ^{(1)} (y) {\rm e}^{{\rm i}\alpha x} + {\rm c.c.}, \end{equation}

and energy equation (6.2c) takes the form

(6.5a–c)\begin{align} D^2 \varTheta_1 ^{(1)} -({\rm i} \alpha Pr Re u_0 - {\rm i} \alpha c Pr+\alpha^2 ) \varTheta_1 ^{(1)}=0, \quad \varTheta_1 ^{(1)} (1)=0,\quad \varTheta_1 ^{(1)} ({-}1) = \tfrac{1}{4} Ra_{p,L}. \end{align}

Equations (6.2a,b) are reduced to a single equation of the form

(6.6)\begin{equation} \nabla ^4 \varPsi_1 -Reu_0 \frac{\partial }{\partial x}(\nabla ^2 \varPsi_1) + Re \frac{{\rm d}^2 u_0}{{{\rm d}y}^2 } \frac{\partial \varPsi_1} {\partial x}+ c \frac{\partial }{\partial x}(\nabla ^2 \varPsi_1)=Pr^{{-}1} \frac{\partial \varTheta_1}{\partial x}, \end{equation}

where $\varPsi _1$ denotes the stream function with $U_1 = {\partial \varPsi _1 }/{\partial y}$ and $V_1 = -{\partial \varPsi _1 }/{\partial x}$. The character of the forcing on the right-hand side of (6.6) suggests a solution in the form

(6.7)\begin{equation} \varPsi_1 (x,y)= \varPsi_1 ^{(1)} (y) {\rm e}^{{\rm i}\alpha x} + {\rm c.c.} \end{equation}

Substitution of (6.4) and (6.7) into (6.6) leads to

(6.8a)\begin{align} &D ^4 \varPsi_1 ^{(1)} - ({\rm i} \alpha Re u_0-{\rm i} \alpha c +2 \alpha ^2) D^2 \varPsi_1 ^{(1)} +({\rm i} \alpha ^3 Re u_0 + {\rm i} \alpha Re D^2 u_0 -{\rm i} \alpha ^3 c+\alpha ^4 ) \varPsi_1 ^{(1)}\nonumber\\ &\quad ={\rm i} \alpha Pr^{{-}1}\varTheta_1 ^{(1)}, \end{align}

(6.8b)\begin{gather} \varPsi_1 ^{(1)}(\pm1)= D\varPsi_1 ^{(1)}(\pm1)=0. \end{gather}

In the above, we assume the right-hand side as $F_1 =\textrm {i}\alpha Pr^{-1} \varTheta _1 ^{(1)}$ which is the $x$-component of the gradient of buoyancy force and acts as a flow forcing. The velocity components have the form

(6.9)\begin{equation} [U_1,V_1 ](x,y)= [ U_1 ^{(1)},V_1 ^{(1)}] (y){\rm e}^{{\rm i}\alpha x} + {\rm c.c.}, \end{equation}

with $U_1 ^{(1)} = D \varPsi _1 ^{(1)}$ and $V_1 ^{(1)} = -\textrm {i} \alpha \varPsi _1 ^{(1)}$. Analysis of $O(\epsilon ^2)$ equations shows that the unknowns can be represented as

(6.10)\begin{equation} [\varTheta_2,U_2,V_2 ](x,y)= [\varTheta_2^{(0)},U_2 ^{(0)},V_2 ^{(0)}] (y) + [ \varTheta_2 ^{(2)},U_2 ^{(2)},V_2 ^{(2)}] (y){\rm e}^{{\rm i}2\alpha x} + {\rm c.c.} \end{equation}

It is easy to show that $V_2 ^{(0)}=0$. Substitution of (6.9) and (6.10) into (6.3a) and extraction of the zero modal function combined with the enforcement of the mean-pressure gradient constraint lead to the following flow problem:

(6.11a,b)\begin{equation} D^2 U_2^{(0)} = V_1 ^{({-}1)} DU_1 ^{(1)} + V_1 ^{(1)} DU_1 ^{({-}1)} , \quad U_2 ^{(0)}({\pm} 1)=0. \end{equation}

Double integration of (6.11a,b) yields

(6.12a)\begin{equation} U_2^{(0)} = \int_{{-}1} ^{y} g(\eta) \,{\rm d}\eta -\tfrac{1}{2} \int_{{-}1} ^{1} (1+y) g(y) \,{{\rm d}y}, \end{equation}

where

(6.12b)\begin{equation} g(y)=V_1 ^{({-}1)} U_1 ^{(1)} + V_1 ^{(1)} U_1 ^{({-}1)}, \end{equation}

and leads to evaluate the flow rate correction $Q_c$ as

(6.13)\begin{equation} Q_c=\int_{{-}1} ^{1} U_2 ^{(0)}\, {{\rm d}y} =\int_{{-}1} ^{1}\int_{{-}1} ^{\eta} g(\eta) \,{\rm d}\eta \,{{\rm d}y}-\int_{{-}1} ^{1} g(y)\, {{\rm d}y}. \end{equation}

In the above, $g(y)$ represents the Reynolds stress created by the buoyancy-induced motion resulting from effect of the thermal wave, and its sign dictates whether $Q_c$ is positive or negative. Numerical solution of (6.5) and (6.8) have been carried out using the collocation method as described in § 3, and integrations present in (6.12) and (6.13) have been performed with an accuracy of fourth-order.

Solution of $\varTheta _1 ^{(1)}$ reveals that the modal functions are purely real in the absence of wave motion or the external flow, but the presence of wave movement or external flow causes this modal function to become complex. Hence the imaginary part, shown in figure 15(a), has two components: wave-induced correction and flow-induced correction. Both corrections contribute to the driving force $F_1$ (see (6.8)) with the flow-induced correction always assisting the bulk flow whereas the wave-induced correction assists for the wave moving opposite to the flow direction (countercurrent wave) and opposes for the wave moving in the flow direction(cocurrent wave) if the wave velocity exceeds certain threshold. The complex modal function $\varTheta _1 ^{(1)}$ produces a phase shift $\varPhi$ with respect to the wave imposed at the lower plate and is shown in figure 15(b). The interplay of wave-induced and flow-induced corrections creates either a negative phase shift causing the net horizontal flow rate to increase (overall resistance reduction in the channel) or a positive phase shift causing the net flow rate to decrease (overall resistance increase in the channel). The phase shift $\varPhi =0$ produces $Q_c =0$.

Figure 15. (a) Distributions of the imaginary $\varTheta _i ^{(1)}$ parts of the temperature modal function $\varTheta _1 ^{(1)}$, (b) the phase shift $\varPhi$ of $\varTheta _1 ^{(1)}$ with respect to the wave at the lower plate and (c) distribution of the Reynolds stress $g(y)$ for $\alpha =2$, $Ra_{p,L}=200$, $Pr=0.71$. In (c), solid, dashed and dotted lines represent $Re=1$ with wave velocity ($c\ne 0$), $Re=1$ with stationary wave ($c=0$), and $Re=0$ with wave velocity ($c\ne 0$), respectively, and the grey shaded zone denotes flow rate increase over the stationary wave limit.

Next, we look into the Reynolds stress developed due to the interaction of the convective flow modifications generated from the thermal waves acting on the lower wall (see figure 15c). A stationary wave as well as a countercurrent wave generate positive Reynolds stress causing the resistance reduction in the channel, but a cocurrent wave (higher than the threshold) creates negative Reynolds stress causing the resistance increase in the channel. Increase or decrease of resistance reduction over the stationary wave limit is dictated by the increase or decrease of the Reynolds stress compared with the Reynolds stress developed by the stationary wave, as depicted by the grey colour in figure 15(c).

Furthermore, small amplitude waves, i.e. $\epsilon = Ra_{p,L} \rightarrow 0$, reveal that the velocity components $U_1 ^{(1)}$ and $V_1 ^{(1)}$ present in the Reynolds stress $g(y)$ are proportional to $Ra_{p,L}$. Hence, the flow rate correction $Q_c$ varies proportionally to $Ra ^2_{p,L}$, as shown in figure 13.

Next, we focus our attention to a weak flow with $Re \rightarrow 0$.

6.2. Weak flow

We assume $Re$ is small but finite, and represent the solutions of (3.1) as

(6.14)\begin{equation} [u,v,\theta,p]=[U_0, V_0,\varTheta_0, P_0]+ Re [U_1, V_1,\varTheta_1, P_1] + O(Re^2). \end{equation}

Substitution of (6.14) into (3.1) results in the following leading-order systems: for $O(1)$ we have

(6.15a)$$\begin{gather} \nabla ^2 U_0+c \frac{\partial U_0 }{\partial x}- U_0\frac{\partial U_0 }{\partial x} - V_0\frac{\partial U_0}{\partial y} -\frac{\partial P_0}{\partial x}=0 , \end{gather}$$

(6.15b)$$\begin{gather}\nabla ^2 V_0+c \frac{\partial V_0 }{\partial x}-U_0\frac{\partial V_0 }{\partial x} - V_0\frac{\partial V_0}{\partial y} -\frac{\partial P_0}{\partial y} + Pr^{{-}1}\varTheta_0= 0, \end{gather}$$

(6.15c,d)$$\begin{gather}Pr^{{-}1} \nabla ^2 \varTheta_0 + c \frac{\partial \varTheta_0 }{\partial x} - U_0\frac{\partial \varTheta_0 }{\partial x} - V_0\frac{\partial \varTheta_0}{\partial y} = 0, \quad \frac{\partial U_0 }{\partial x} + \frac{\partial V_0}{\partial y} = 0, \end{gather}$$

which describes the system that produces a pumping effect by thermal waves with a net horizontal flow rate $Q_{00} = \int _{-1} ^{+1} U_0 \,{\textrm {d}y}$ (Hossain & Floryan 2023); for $O(Re)$ we have

(6.16a)$$\begin{gather} \nabla ^2 U_1 +c \frac{\partial U_1 }{\partial x} - U_0\frac{\partial U_1 }{\partial x} -U_1\frac{\partial U_0 }{\partial x}-V_0\frac{\partial U_1 }{\partial y} - V_1\frac{\partial U_0}{\partial y} -\frac{\partial P_1}{\partial x} = u_0\frac{\partial U_0 }{\partial x}+V_0 \frac{\partial u_0 }{\partial y}, \end{gather}$$

(6.16b)$$\begin{gather}\nabla ^2 V_1 + c\frac{\partial V_1 }{\partial x}- U_0\frac{\partial V_1 }{\partial x} -U_1\frac{\partial V_0 }{\partial x}- V_0\frac{\partial v_1}{\partial y} - V_1\frac{\partial V_0}{\partial y} -\frac{\partial P_1}{\partial y}+ Pr^{{-}1} \varTheta_1 = u_0\frac{\partial V_0 }{\partial x}, \end{gather}$$

(6.16c)$$\begin{gather}Pr^{{-}1} \nabla ^2\varTheta_1 + c\frac{\partial \varTheta_1 }{\partial x}- U_0\frac{\partial \varTheta_1 }{\partial x} -U_1\frac{\partial \varTheta_0 }{\partial x} - V_0\frac{\partial \varTheta_1}{\partial y} - V_1\frac{\partial \varTheta_0}{\partial y} = u_0 \frac{\partial \varTheta_0}{\partial x}, \end{gather}$$

(6.16d)$$\begin{gather}\frac{\partial U_1 }{\partial x} + \frac{\partial V_1}{\partial y} = 0, \end{gather}$$

where $u_0=1-y^2$ is the reference isothermal flow whose effects are evident in the right-hand side of (6.16a–c) and acts as a forcing function which certainly provides a non-zero $U_1$. Therefore, the flow rate correction can be represented as

(6.17)\begin{equation} Q_c = \int_{{-}1} ^{{+}1} (U_0 + Re U_1)\, {{\rm d}y} + O(Re^2) = Q_{00}+Re Q_{1} + O(Re^2), \end{equation}

with $Q_{00}$ representing flow rate at $Re=0$ and $Q_{1}$ representing flow rate modification due to the presence of reference flow. Figure 10 demonstrates that, for $c\ne 0$, $Q_c$ approaches a well-defined limit $Q_{00}$ as $Re\rightarrow 0$.

The case $c=0$ is special as it does not produce any pumping in the limit $Re\rightarrow 0$ and separates conditions leading to positive and negative $c$ (see figure 10). We assume the unknowns present in (6.5) and (6.8) as

(6.18)\begin{equation} [\varTheta_1 ^{(1)}, \varPsi_1 ^{(1)} ]=[\hat{\varTheta}_0, \hat{\varPsi}_0] + Re [\hat{\varTheta}_1, \hat{\varPsi}_1]+ Re^2 [\hat{\varTheta}_2, \hat{\varPsi}_2] + O(Re^3). \end{equation}

Substitution of (6.18) into (6.5) and (6.8) leads to the following: for $O(1)$ we have

(6.19a,b)\begin{equation} D^2 \hat{\varTheta}_0 -\alpha^2 \hat{\varTheta}_0 =0, \quad D ^4 \hat{ \varPsi}_0 -2 \alpha ^2 D^2 \hat{\varPsi}_0 +\alpha ^4 \hat{\varPsi}_0 ={\rm i}\alpha Pr^{{-}1} \hat{\varTheta}_0; \end{equation}

and for $O(Re)$ we have

(6.19c)$$\begin{gather} D^2 \hat{\varTheta}_1 -\alpha^2 \hat{\varTheta}_1 ={\rm i} \alpha Pr u_0 \hat{\varTheta}_0, \end{gather}$$

(6.19d)$$\begin{gather}D ^4 \hat{ \varPsi}_1 -2 \alpha ^2 D^2 \hat{\varPsi}_1 +\alpha ^4 \hat{\varPsi}_1 ={\rm i} \alpha Pr^{{-}1} \hat{\varTheta}_1 + {\rm i} \alpha u_0 D^2 \hat{\varPsi}_0-({\rm i}\alpha^3 u_0 +{\rm i} \alpha D^2 u_0) \hat{\varPsi}_0. \end{gather}$$

The analytical solution of (6.19a) reads

(6.20a,b)\begin{equation} \hat{\varTheta}_0 = Ra_{p,L} \frac{\sinh(\vartheta(1- y))}{4 \sinh (2\vartheta)} {\rm e}^{{\rm i} \alpha x}, \quad \vartheta=\sqrt(\alpha ^2-{\rm i} c \alpha Pr), \end{equation}

whereas (6.19b–d) warrant a numerical solution. Nevertheless, a qualitative analysis can be performed by assuming $\hat {\varTheta }_0 = \hat {\varTheta }_{r0} +\textrm {i}\hat {\varTheta }_{i0}, \hat {\varTheta }_1 = \hat {\varTheta }_{r1} +\textrm {i}\hat {\varTheta }_{i1}, \hat {\varPsi }_0 = \hat {\varPsi }_{r0} +\textrm {i}\hat {\varPsi }_{i0}, \hat {\varPsi }_1 = \hat {\varPsi }_{r1} +\textrm {i}\hat {\varPsi }_{i1},$ and separating real and imaginary parts of the resulting equations, which reveals that $\hat {\varTheta }_{i0}=0$, $\hat {\varPsi }_{r0}=0$, $\hat {\varPsi }_{i1}=0$. Further simplification provides the velocity components as $U_1 ^{(1)}= ReD\hat {\varPsi }_{r1} + O(Re^3) + \textrm {i} [D\hat {\varPsi }_{i0}+O(Re^2)]$ and $V_1 ^{(1)}= \alpha \hat {\varPsi }_{i0} + O(Re^2) + \textrm {i} [-\alpha Re\hat {\varPsi }_{r1}+O(Re^3)]$, leading to the form of the Reynolds stress function as

(6.21)\begin{equation} g(y) = 2Re\hat{\varPsi}_{i0}D\hat{\varPsi}_{r1} + O(Re^2), \end{equation}

which demonstrates that the flow rate correction $Q_c$ increases proportionally to $Re$ as shown in figure 10 for $c=0$.

6.3. Long-wavelength waves

In order to gain further insight of the flow mechanism we consider long-wavelength waves that correspond to the limit $\alpha \rightarrow 0$. Introduce a wave-wavelength-based scale $\xi = \alpha x$, and represent the unknowns as expansions in terms of $\alpha$ as

(6.22a)$$\begin{gather} [u(\xi,y),v(\xi,y)]=\sum_{n=1} ^{4} \alpha ^n [U_n (\xi,y),V_n (\xi,y)]+O(\alpha^5), \end{gather}$$

(6.22b)$$\begin{gather} {[\theta(\xi,y),p(\xi,y)]}=\sum_{n=0} ^{3} \alpha ^n [\varTheta_n(\xi,y),P_n (\xi,y)]+O(\alpha^4). \end{gather}$$

Substitution of (6.22) into field equations (3.1) and extraction of the leading-order terms results in the following system:

(6.23a–d)$$\begin{gather} \frac{\partial^2 \varTheta_0}{\partial y^2}=0, \quad \frac{\partial P_0}{\partial y}=\frac{\varTheta_0}{Pr}, \quad \frac{\partial^2 U_1}{\partial y^2}=\frac{\partial P_0}{\partial \xi}, \quad \frac{\partial V_1}{\partial y}=0, \end{gather}$$

(6.23e–h)$$\begin{gather}\varTheta_0({-}1)=0.5 Ra_{p,L}\cos(\alpha x), \quad \varTheta_0(1)=0,\quad U_1({\pm} 1)=V_1({\pm} 1)=0,\quad\left. {\partial P_0}/{\partial \xi} \right|_{m}= 0. \end{gather}$$

Its solution is given as

(6.24a–c)\begin{equation} \varTheta_0=\frac{1}{4} Ra_{p,L} H_{\varTheta,01} (y)\cos \xi, \quad U_1=\frac{Ra_{p,L}}{480Pr} H_{U,11} (y) \sin\xi, \quad V_1=0, \end{equation}

where the coefficients $H_{\varTheta,01}$ and $H_{U,11}$ are polynomials in $y$, and given in Appendix C. Both temperature and the horizontal velocity are periodic and unaffected by the wave and the external flow.

The next order of system,

(6.25a–d)\begin{gather} \left.\begin{gathered} \frac{\partial^2 \varTheta_1}{\partial y^2}=RePr u_0\frac{\partial \varTheta_0}{\partial \xi}-cPr\frac{\partial \varTheta_0}{\partial \xi}, \quad \frac{\partial P_1}{\partial y}=\frac{\varTheta_1}{Pr},\\ \frac{\partial^2 U_2}{\partial y^2}=\frac{\partial P_1}{\partial \xi}+Reu_0\frac{\partial U_1}{\partial \xi}+V_2Re\frac{{\rm d} u_0}{{\rm d}y} -c\frac{\partial U_1}{\partial \xi}, \quad \frac{\partial U_1}{\partial \xi} +\frac{\partial V_2}{\partial y}=0, \end{gathered}\right\} \end{gather}

(6.25e–g)\begin{gather} \varTheta_1({\pm} 1)=0,\quad U_2({\pm} 1)=V_2({\pm} 1)=0,\quad\left. {\partial P_1}/{\partial \xi} \right|_{m}= 0, \end{gather}

has the following solution:

(6.26)\begin{align} \left.\begin{gathered} \varTheta_1=\frac{1}{240} Pr Ra_{p,L} [H_{\varTheta,11} (y) Re + H_{\varTheta,12} (y) c ] \sin \xi,\\ U_2={-}\frac{Ra_{p,L}}{403\,200Pr}\left[ \left [H_{U,21} (y) +PrH_{U,22}(y)\right ] Re + \left [H_{U,23} (y) +PrH_{U,24}(y)\right ] c \right]\cos \xi,\\ V_2={-}\frac{Ra_{p,L}}{480Pr} H_{V,21} (y)\cos \xi, \end{gathered}\!\right\} \end{align}

with definitions of all coefficients given in Appendix C. At this level of approximation, the external flow and the wave generate temperature corrections which produce corrections in horizontal fluid motion. The complementary vertical fluid motion (due to continuity) is a consequence of the previous horizontal velocity correction. All corrections are still periodic.

The next order of system,

(6.27a,b)\begin{gather} \left.\begin{gathered} \frac{\partial^2 \varTheta_2}{\partial y^2}=RePr u_0\frac{\partial \varTheta_1}{\partial \xi}-cPr\frac{\partial \varTheta_1}{\partial \xi} + Pr U_1 \frac{\partial \varTheta_0}{\partial \xi} + Pr V_2 \frac{\partial \varTheta_0}{\partial y}-\frac{\partial^2 \varTheta_0}{\partial y^2},\\ \frac{\partial P_2}{\partial y}=\frac{\partial^2 V_2}{\partial y^2}+\frac{\varTheta_2}{Pr}, \end{gathered}\right\} \end{gather}

(6.27c,d)\begin{gather} \left.\begin{gathered} \frac{\partial^2 U_3}{\partial y^2}=\frac{\partial P_2}{\partial \xi}+Re u_0\frac{\partial U_2}{\partial \xi}+V_3 Re \frac{{\rm d} u_0}{{\rm d}y}-c\frac{\partial U_2}{\partial \xi}-\frac{\partial^2 U_1}{\partial \xi^2}+U_1 \frac{\partial U_1}{\partial \xi} +V_2 \frac{\partial U_1}{\partial y}, \\ \frac{\partial U_2}{\partial \xi} +\frac{\partial V_3}{\partial y }=0, \end{gathered}\right\} \end{gather}

(6.27e–g)\begin{gather} \varTheta_2({\pm} 1)=0,\quad U_3({\pm} 1)=V_3({\pm} 1)=0,\quad \left.{\partial P_2}/{\partial \xi} \right|_{m}= 0, \end{gather}

has solution of the form

(6.28) \begin{gather} \left.\begin{aligned} \varTheta_2&={-}\frac{Ra_{p,L}}{403\,200} \left[ Ra_{p,L} H_{\varTheta,20} (y) + \{ H_{\varTheta,21} (y) + Pr^2 [H_{\varTheta,22} (y) Re^2 + H_{\varTheta,23} (y) cRe\right.\\ &\quad +\left. H_{\varTheta,24} (y) c^2 ] \} \cos \xi + Ra_{p,L} H_{\varTheta,25} (y) \cos(2 \xi) \right],\\ U_3&= Ra_{p,L} \left[ c^2 [Pr H_{U,31} (y)+H_{U,32}(y)] + \frac{1}{Pr}[H_{U,33} (y)+ c^2 H_{U,34}(y)] \right] \sin \xi\\ &\quad +\, \frac{Ra_{p,L}^2}{Pr^2} [PrH_{U,35} (y)+H_{U,36} (y) ] \sin(2 \xi) ,\\ V_3&={-}\frac{Ra_{p,L}}{1\,209\,600Pr}\left [ \left [H_{V,31} (y) +Pr H_{V,32} \right ] Re + \left [H_{V,33} (y) +Pr H_{V,34} \right ] c \right]\sin \xi, \end{aligned}\right\} \end{gather}

with definitions of all coefficients (except for $U_3$ due to length) given in Appendix C. An aperiodic part (first term of the $\varTheta _2$ solution) is produced in the temperature correction, whereas the velocity corrections are still purely periodic. As we are interested in the aperiodic velocity correction, it is sufficient to consider the following equations for the next order of the system:

(6.29a)\begin{align} \frac{\partial^2 U_4}{\partial y^2}&=\frac{\partial P_3}{\partial \xi}+Re u_0\frac{\partial U_3}{\partial \xi}+V_4 Re \frac{{\rm d} u_0}{{\rm d}y} -c\frac{\partial U_3}{\partial \xi}-\frac{\partial^2 U_2}{\partial \xi^2}+U_1 \frac{\partial U_2}{\partial \xi}+U_2 \frac{\partial U_1}{\partial \xi} \nonumber\\ &\quad +V_2 \frac{\partial U_2}{\partial y}+V_3 \frac{\partial U_1}{\partial y}, \end{align}

(6.29b,c)\begin{align} U_4({\pm} 1)&=0,\quad \left.{\partial P_3}/{\partial \xi} \right|_{m}= 0. \end{align}

The last four terms $F(y) = U_1 ({\partial U_2}/{\partial \xi })+U_2 ({\partial U_1}/{\partial \xi }) +V_2 ({\partial U_2}/{\partial y})+V_3 ({\partial U_1}/{\partial y})$ of (6.29a) provide an aperiodic forcing which is capable of producing an aperiodic velocity correction $U_{4,ap}$ which can be expressed as

(6.30a)\begin{equation} U_{4,ap}= \int_{{-}1} ^{y} \int_{{-}1}^{\mu} F(\eta) \,{\rm d}\eta \,{\rm d}\mu -\frac{y+1}{2} \int_{{-}1} ^{1} \int_{{-}1}^{\mu} F(\eta) \,{\rm d}\eta \,{\rm d}\mu , \end{equation}

and reduced after integration to

(6.30b)\begin{align} U_{4,ap}&= \frac{Ra_{p,L}^2}{8\,717\,829\,120\,000Pr^2} \left[\left[H_{U,41} (y) + Pr H_{U,42}(y)\right ] Re \right.\nonumber\\ &\quad + \left.\left[H_{U,43} (y) + Pr H_{U,44}(y) \right] c \right], \end{align}

giving the flow rate correction

(6.31) \begin{align} Q_{c,ap} = \int_{{-}1} ^{1} U_{4,ap} \,{{\rm d}y} = \frac{\alpha ^4 Ra_{p,L}^2}{12\,770\,257\,500Pr^2 } \left[(1929+3130Pr)Re-3435(1+Pr)c\right]. \end{align}

Definitions of $H_{U,41-44}$ are given in Appendix C. The flow rate correction is proportional to ${\sim }\alpha ^4$ and this limit is shown in figure 11 and has two components: one associated with the flow $Re$ and the other associated with the wave velocity $c$. Countercurrent waves produce positive corrections at all $Re$ and $c$. Cocurrent waves produce $Q_c=0$ at the critical velocity $c_n=(1929+3130Pr)Re/3435(1+Pr)$ and critical Reynolds number $Re_n=3435(1+Pr)c/(1929+3130Pr)$; waves with $c< c_n$ and $Re>Re_n$ produce positive corrections and waves with $c>c_n$ and $Re< Re_n$ produce negative corrections.

The net shear force correction can be calculated as

(6.32)\begin{equation} \tau_{L,net} = \frac{ Ra_{p,L} ^2\alpha ^4 }{1\,702\,701\,000 Pr^2} \left[3(17+717 Pr)Re - 143(3+17Pr)c\right]={-}\tau_{U,net} . \end{equation}

Next, we focus our attention to the short wavelength heating, as again, this case can be solved analytically.

6.4. Short wavelength waves

Consider short wavelength waves that correspond to $\alpha \rightarrow \infty$, and in this limit, the conduction temperature field is approximated as $\theta _0 = \frac {1}{2} Ra_{p,L}\textrm {e}^{-\alpha (1+y)} \cos (\alpha x),$ demonstrating formation of a thin boundary layer close to the lower wall. Introduce a wavelength-related scale $\xi =\alpha x$ in the streamwise direction and a stretched scale $\varOmega = \alpha (1+y)$ along the spanwise direction and express the solution in the inner layer in terms of the following expansions as

(6.33a)$$\begin{gather} [u_{in},v_{in},\theta_{in}]=\sum_{n=1} ^{6}\alpha^{{-}n} [U_n(\xi,\varOmega),V_n(\xi,\varOmega),\varTheta_n(\xi,\varOmega)]+O(\alpha^{{-}7}), \end{gather}$$

(6.33b)$$\begin{gather} {[p_{in}]}=\sum_{n=0} ^{5} \alpha^{{-}n}[P_n(\xi,\varOmega)]+O(\alpha^{{-}6}). \end{gather}$$

Substitution of (6.33) into (3.1) and retention of the leading-order terms result in the following $O(\alpha ^{-1} )$ system:

(6.34a,b)$$\begin{gather} \frac{\partial^2 U_1}{\partial \xi^2}+\frac{\partial^2 U_1}{\partial \varOmega^2} -\frac{\partial P_0}{\partial \xi}=0, \quad \frac{\partial^2 V_1}{\partial \xi^2}+\frac{\partial^2 V_1}{\partial \varOmega^2} -\frac{\partial P_0}{\partial \varOmega}=0, \end{gather}$$

(6.34c)$$\begin{gather}\frac{\partial^2 \varTheta_1}{\partial \xi^2}+\frac{\partial^2 \varTheta_1}{\partial \varOmega^2} = \frac{1}{2} cPr Ra_{p,L} {\rm e}^{-\varOmega} \sin \xi, \end{gather}$$

(6.34d–f)$$\begin{gather}U_1({-}1)=V_1({-}1)=0,\quad \varTheta_1({-}1)=0,\quad\left. {\partial P_0}/{\partial \xi} \right|_{m}= 0, \end{gather}$$

and its solution, which can be determined using method of separation of variables, has the form

(6.34g–i)\begin{equation} U_1=0, \quad V_1=0, \quad \varTheta_1={-}\tfrac{1}{4}c Pr Ra_{p,L} \varOmega {\rm e}^{-\varOmega} \sin\xi . \end{equation}

One can observe that only the wave, not the external flow, affects the temperature, resulting in no convection. System $O(\alpha ^{-2} )$ has the following form:

(6.35a,b)$$\begin{gather} \frac{\partial^2 U_2}{\partial \xi^2}+\frac{\partial^2 U_2}{\partial \varOmega^2} -\frac{\partial P_1}{\partial \xi}=0, \quad \frac{\partial^2 V_2}{\partial \xi^2}+\frac{\partial^2 V_2}{\partial \varOmega^2} -\frac{\partial P_1}{\partial \varOmega}={-}\frac{Ra_{p,L}}{2Pr} {\rm e}^{-\varOmega} \cos\xi , \end{gather}$$

(6.35c)$$\begin{gather}\frac{\partial^2 \varTheta_2}{\partial \xi^2}+\frac{\partial^2 \varTheta_2}{\partial \varOmega^2} ={-}RePrRa_{p,L} \varOmega {\rm e}^{-\varOmega} \sin \xi -cPr \frac{\partial \varTheta_1}{\partial \xi}, \end{gather}$$

(6.35d–f)$$\begin{gather}U_2({-}1)=V_2({-}1)=0,\quad \varTheta_2({-}1)=0,\quad\left. {\partial P_1}/{\partial \xi} \right|_{m}= 0, \end{gather}$$

and its solution can be written as

(6.35g–h)$$\begin{gather} U_2=\frac{Ra_{p,L}}{16Pr} \varOmega ({-}2+\varOmega) {\rm e}^{-\varOmega} \sin\xi , \quad V_2=\frac{Ra_{p,L}}{16Pr} \varOmega^2 {\rm e}^{-\varOmega} \cos\xi, \end{gather}$$

(6.35i)$$\begin{gather}\varTheta_2= \frac{1}{16} Pr Ra_{p,L} \varOmega (1+\varOmega) {\rm e}^{-\varOmega} \left[4 Re \sin\xi - Pr c^2 \cos\xi \right]. \end{gather}$$

At this level of approximation, both the external flow and the wave affect the temperature resulting in a periodic motion. System $O(\alpha ^{-3})$ has the following form:

(6.36a,b)$$\begin{align} \frac{\partial^2 U_3}{\partial \xi^2}+\frac{\partial^2 U_3}{\partial \varOmega^2} -\frac{\partial P_2}{\partial \xi}&={-}c\frac{\partial U_2}{\partial \xi}, \quad \frac{\partial^2 V_3}{\partial \xi^2}+\frac{\partial^2 V_3}{\partial \varOmega^2} -\frac{\partial P_2}{\partial \varOmega}={-}c\frac{\partial V_2}{\partial \xi}-\frac{\varTheta_1}{Pr}, \end{align}$$

(6.36c)$$\begin{align}\frac{\partial^2 \varTheta_3}{\partial \xi^2}+\frac{\partial^3 \varTheta_3}{\partial \varOmega^2} &= 2RePr \varOmega \frac{\partial \varTheta_1}{\partial \xi} + \frac{1}{2} Pr Ra_{p,L} {\rm e}^{-\varOmega} [(Re \varOmega ^2 -U_2 )\sin\xi -V_2 \cos\xi]\nonumber\\&\quad -cPr \frac{\partial \varTheta_2}{\partial \xi} , \end{align}$$

(6.36d–f)$$\begin{align}U_3({-}1)&=V_3({-}1)=0, \quad\varTheta_3({-}1)=0,\quad {\partial P_2}/{\partial \xi}|_{m}= 0, \end{align}$$

and its solution can be written as

(6.36g,h)\begin{align} U_3&=\frac{c Ra_{p,L}}{192Pr} {\rm e}^{-\varOmega} K_{U3} \cos\xi, \quad V_3={-}\frac{cRa_{p,L}}{192Pr} {\rm e}^{-\varOmega} K_{V3} \sin\xi, \end{align}

(6.36i)\begin{align} \varTheta_3&= \frac{1}{256} [Ra_{p,L}^2 +256 B_2\varOmega] -\frac{1}{512} Ra_{p,L}^2 {\rm e}^{{-}2\varOmega} [K_{\varTheta 31} + K_{\varTheta 32} \cos(2 \xi) ]\nonumber\\ &\quad -\frac{1}{96}Ra_{p,L} Pr\varOmega {\rm e}^{-\varOmega}\{ 4 Re K_{\varTheta 33} \sin\xi + cPr^2[ (c^2 K_{\varTheta 34}-4Re K_{\varTheta 33}) \cos\xi\nonumber\\ &\quad -4 Re K_{\varTheta 34} \sin \xi ]\}, \end{align}

with $K_{U3}=\varOmega [-6-3\varOmega +2\varOmega ^2 +2Pr (-6+\varOmega ^2)]$, $K_{V3}=\varOmega ^2 [3+2\varOmega +2Pr(3+\varOmega )]$, $K_{\varTheta 31} =2(1+2\varOmega +2\varOmega ^2)$, $K_{\varTheta 32} =\varOmega (1+2\varOmega )$, $K_{\varTheta 33} =3+3\varOmega +2\varOmega ^2$ and $K_{\varTheta 34} =3+3\varOmega +\varOmega ^2$. The velocity field remains periodic, whereas the temperature field produces a net heat transfer between the plates described by the first bracketed term in $\varTheta _3$ and the constant $B_2$ in this term is to be calculated from the matching with the outer solution. The system $O(\alpha ^{-4})$ has the following form:

(6.37a)\begin{gather} \frac{\partial^2 U_4}{\partial \xi^2}+\frac{\partial^2 U_4}{\partial \varOmega^2} -\frac{\partial P_3}{\partial \xi}=2Re \varOmega \frac{\partial U_2}{\partial \xi} +2Re V_2 -c\frac{\partial U_3}{\partial \xi}, \end{gather}

(6.37b)\begin{gather}\frac{\partial^2 V_4}{\partial \xi^2}+\frac{\partial^2 V_4}{\partial \varOmega^2} -\frac{\partial P_3}{\partial \varOmega}=2Re \varOmega\frac{\partial V_2}{\partial \xi} -c\frac{\partial V_3}{\partial \xi}-\frac{\varTheta_2}{Pr}, \end{gather}

(3.37c)\begin{align} \frac{\partial^2 \varTheta_4}{\partial \xi^2}+\frac{\partial^3 \varTheta_4}{\partial \varOmega^2} &= 2Re Pr \varOmega \frac{\partial \varTheta_2}{\partial \xi}-Re Pr \varOmega^2 \frac{\partial \varTheta_1}{\partial \xi} -cPr \frac{\partial \varTheta_3}{\partial \xi} \nonumber\\ &\quad+Pr\left[U_2 \frac{\partial \varTheta_1}{\partial \xi}+V_2 \frac{\partial \varTheta_1}{\partial \varOmega}\right]\nonumber\\ &\quad - \frac{1}{2}Pr Ra_{p,L} {\rm e}^{-\varOmega} [U_3 \sin\xi +V_3 \cos\xi], \end{align}

(6.37d–f)\begin{gather} U_4({-}1)=V_4({-}1)=0,\quad \varTheta_4({-}1)=0,\quad \partial P_3/{\partial \xi}|_{m}= 0, \end{gather}

whose solution can be written as

(6.37g)$$\begin{align} U_4&={-}\frac{ Ra_{p,L}{\rm e}^{-\varOmega}}{768Pr}[ Re (K_{U41}+Pr K_{U42})\cos \xi \nonumber\\ &\quad+c^2 (K_{U43} +Pr K_{U44}+Pr^2K_{U45})\sin\xi], \end{align}$$

(6.37h)$$\begin{align}V_4 &={-}\frac{ Ra_{p,L}{\rm e}^{-\varOmega}}{768Pr} [{-}Re (K_{V41}+Pr K_{V42}) \sin \xi \nonumber\\ &\quad+ c^2(K_{V43} +Pr K_{V44}+Pr^2K_{V45}) \cos\xi], \end{align}$$

(6.37i)\begin{align} \varTheta_4&= \frac{ Pr^2 Ra_{p,L} {\rm e}^{-\varOmega}}{768} [Re (c^2 Pr K_{\varTheta 41} - c K_{\varTheta 42}-ReK_{\varTheta 42}) \cos \xi \nonumber\\ &\quad + c^2 Pr (c^2 Pr K_{\varTheta 41} - Re K_{\varTheta 44}) \sin \xi]\nonumber\\ &\quad - \frac{c Ra_{p,L}^2 {\rm e}^{{-}2\varOmega}}{12\,288} [K_{\varTheta 45} + Pr K_{\varTheta 46}] \sin(2 \xi), \end{align}

with $K_{U41}=6\varOmega (-18-3\varOmega +\varOmega ^3)$, $K_{U42}=4\varOmega (-30-3\varOmega +2\varOmega ^2+\varOmega ^3)$, $K_{U43}=\varOmega (-12-6\varOmega +\varOmega ^3)$, $K_{U44}=\varOmega (-18-9\varOmega +2\varOmega ^2+\varOmega ^3)$, $K_{U45}=\varOmega (-30-3\varOmega +2\varOmega ^2+\varOmega ^3)$, $K_{V41}=6\varOmega ^2 (9+ 4\varOmega +\varOmega ^2)$, $K_{V42}=4\varOmega ^2 (15+ 6\varOmega +\varOmega ^2)$, $H_{V43}= \varOmega ^2(6 +4\varOmega +\varOmega ^2)$, $H_{V44}=\varOmega ^2(3+\varOmega )^2$, $K_{V45}=\varOmega ^2(15 +6\varOmega + \varOmega ^2)$, $K_{\varTheta 41} = 4\varOmega (15+15\varOmega +6 \varOmega ^2 + \varOmega ^3 )$, $K_{\varTheta 42} =16\varOmega (9+9\varOmega +5\varOmega ^2+2\varOmega ^3)$, $K_{\varTheta 43} =16\varOmega (15+ 15 \varOmega +10 \varOmega ^2 + 3\varOmega ^3 )$, $K_{\varTheta 44} =4\varOmega (33+33\varOmega +18\varOmega ^2+5\varOmega ^3)$, $K_{\varTheta 45}=\varOmega (9+ 18 \varOmega + 8 \varOmega ^2)$ and $K_{\varTheta 46}= 24 \varOmega (1+\varOmega )^2$. The velocity field is still periodic, so we look into the order $O(\alpha ^{-5})$ system which has the following form:

(6.38a)\begin{align} \frac{\partial^2 U_5}{\partial \xi^2}+\frac{\partial^2 U_5}{\partial \varOmega^2} -\frac{\partial P_4}{\partial \xi}&=2Re \varOmega \frac{\partial U_3}{\partial \xi}- Re \varOmega^2 \frac{\partial U_2}{\partial \xi}+2Re V_3-2Re \varOmega V_2-c\frac{\partial U_4}{\partial \xi}\nonumber\\ &\quad +U_2 \frac{\partial U_2}{\partial \xi} +V_2 \frac{\partial U_2}{\partial \varOmega}, \end{align}

(6.38b)\begin{align} \frac{\partial^2 V_5}{\partial \xi^2}+\frac{\partial^2 V_5}{\partial \varOmega^2} -\frac{\partial P_4}{\partial \varOmega}&=2Re \varOmega \frac{\partial V_3}{\partial \xi}- Re \varOmega^2 \frac{\partial V_2}{\partial \xi}-c\frac{\partial V_4}{\partial \xi}+U_2 \frac{\partial V_2}{\partial \xi}\nonumber\\ &\quad+V_2 \frac{\partial V_2}{\partial \varOmega}-\frac{\varTheta_3}{Pr}, \end{align}

(6.38c)\begin{align} \frac{\partial^2 \varTheta_5}{\partial \xi^2}+\frac{\partial^3 \varTheta_5}{\partial \varOmega^2} &= 2RePr\varOmega \frac{\partial \varTheta_3}{\partial \xi}-RePr\varOmega^2 \frac{\partial \varTheta_2}{\partial \xi} -cPr \frac{\partial \varTheta_4}{\partial \xi} \nonumber\\ &\quad +Pr\left[U_2 \frac{\partial \varTheta_2}{\partial \xi}+U_3 \frac{\partial \varTheta_1}{\partial \xi}+V_2 \frac{\partial \varTheta_2}{\partial \varOmega}+V_3 \frac{\partial \varTheta_1}{\partial \varOmega}\right]\nonumber\\ &\quad - \frac{1}{2}Pr Ra_{p,L} {\rm e}^{-\varOmega} [U_4 \sin\xi +V_4 \cos\xi], \end{align}

(6.38d–f)\begin{align} U_5({-}1)&=V_5({-}1)=0, \quad\varTheta_5({-}1)=0,\quad {\partial P_4}/{\partial \xi} |_{m}= 0. \end{align}

The above system still provides only a periodic velocity field, and does not contribute to the next-order aperiodic velocity. Hence it is necessary to analyse the $\xi$-momentum equation in the $O(\alpha ^{-6})$ system, i.e.

(6.39a)\begin{align} \frac{\partial^2 U_6}{\partial \xi^2}+\frac{\partial^2 U_6}{\partial \varOmega^2} -\frac{\partial P_5}{\partial \xi}&=2Re \varOmega \frac{\partial U_4}{\partial \xi}- Re \varOmega^2 \frac{\partial U_3}{\partial \xi}+2Re V_4-2Re \varOmega V_3-c\frac{\partial U_5}{\partial \xi}\nonumber\\ &\quad +U_2 \frac{\partial U_3}{\partial \xi}+U_3 \frac{\partial U_2}{\partial \xi} +V_2 \frac{\partial U_3}{\partial \varOmega}+V_3 \frac{\partial U_2}{\partial \varOmega}. \end{align}

(6.39b,c)\begin{align} U_6({-}1)&=0,\quad {\partial P_5}/{\partial \xi} |_{m}= 0. \end{align}

The last four terms of the right-hand side of (6.39a) are aperiodic, and the aperiodic part of the solution $U_{6,aper}$ can easily be determined as

(6.40)\begin{equation} U_{{6,aper}} =B_3 \varOmega -\frac{cRa_{p,L}^2 (1+Pr)}{4096 Pr^2}\left[1-\frac{1}{3}(3+6\varOmega+6\varOmega^2+4\varOmega^3+2\varOmega^4){\rm e}^{{-}2\varOmega}\right]. \end{equation}

The constant $B_3$ needs to be determined by matching with the outer solution.

The above aperiodic solution does not capture the effect of $Re$, hence we consider the $\xi$-momentum equation in the $O(\alpha ^{-7})$ system,

(6.41a)\begin{align} \frac{\partial^2 U_7}{\partial \xi^2}+\frac{\partial^2 U_7}{\partial \varOmega^2} -\frac{\partial P_6}{\partial \xi}&=2Re \varOmega \frac{\partial U_5}{\partial \xi}- Re \varOmega ^2 \frac{\partial U_4}{\partial \xi} + 2Re V_5 -2Re \varOmega V_4 -c\frac{\partial U_6}{\partial \xi}\nonumber\\ &\quad + U_2 \frac{\partial U_4}{\partial \xi}+U_3 \frac{\partial U_3}{\partial \xi} +U_4 \frac{\partial U_2}{\partial \xi} + V_2 \frac{\partial U_4}{\partial \varOmega}\nonumber\\ &\quad+V_3 \frac{\partial U_3}{\partial \varOmega}+V_4 \frac{\partial U_2}{\partial \varOmega}. \end{align}

(6.41b,c)\begin{align} U_7({-}1)&=0,\quad {\partial P_5}/{\partial \xi} |_{m}= 0. \end{align}

Since the outer solution is invariant in $x$, we assume the outer solution as

(6.42a–c) \begin{equation} \left.\begin{gathered} u_{outer} (x,y)= \alpha ^{{-}6} \hat{U}_6 +\alpha ^{{-}7} \hat{U}_7 + O(\alpha^{{-}8}), \quad v_{outer} (x,y)=0, \\ \theta_{outer} (x,y)= \alpha ^{{-}3} \hat{\varTheta}_3 + O(\alpha^{{-}4}). \end{gathered}\right\} \end{equation}

Substitution of (6.42) into the field equations leads to

(6.43a–c) \begin{equation} \frac{\partial^2 \hat{U}_6}{\partial y^2} =0, \quad \frac{\partial^2 \hat{U}_7}{\partial y^2} =0, \quad \frac{\partial^2 \hat{\varTheta}_3}{\partial y^2} =0, \end{equation}

whose solutions have the form

(6.43d–f) \begin{equation} \hat{U}_6(y) =\hat{A}_6(y-1), \quad \hat{U}_7(y) =\hat{A}_7(y-1), \quad \hat{\varTheta}_3(y) =\hat{A}_3 (y-1). \end{equation}

Constants $\hat {A}_3$, $\hat {A}_6$ and $\hat{A}_7$ are determined from the matching with the inner solution, and the matching process provides

(6.44)\begin{equation} u_{outer} =\frac{Ra_{p,L}^2 }{32\,768 Pr^2} (y-1)[4c(1+Pr)\alpha ^{{-}6}-Re (27+22 Pr) \alpha ^{{-}7}] + O(\alpha ^{{-}8}). \end{equation}

Therefore, the flow rate correction

(6.45)\begin{equation} Q_c =\frac{Ra_{p,L}^2 \alpha ^{{-}7}}{16\,384 Pr^2} \left[{-}4c (1+Pr) \alpha + Re (27+22 Pr) \right] + O(\alpha ^{{-}8}), \end{equation}

and this large $\alpha$ limit is shown in figure 11. The flow rate correction $Q_c$ is negative for a wave with wave velocity $c> Re (27+22 Pr)/4\alpha (1+Pr)$.

7. Verification of flow stability

Having insight into the flow responses and the underlying flow mechanisms, we now examine the stability of the flow in the parameter range considered in the analysis. The formulation of the stability problem is given in § 4. If the flow undergoes a transition to a secondary state, the prediction of the flow rate correction is invalid, and further study, which is beyond the scope of this study, is required. Hence, here, we focused on the onset conditions of a secondary state. We have tested the flow for three possible instability modes: travelling two-dimensional wave ($\beta =0$), transverse roll ($\delta =0$) and oblique roll ($\beta \ne 0, \delta \ne 0$). A sample stability result is shown in figure 16. The stability properties strongly depend on the wave properties, i.e. wave velocity, wave number, amplitude and the flow Reynolds number. The results are presented using wave velocity, wavenumber and Reynolds number as the main parameters and solving the linear stability problem to determine the maximum wave amplitude, guaranteeing flow stability. It was determined that the flow remains stable for the whole range of parameters of interest if the wave amplitude $Ra_{p,L}$ does not exceed 2000. We conclude that the flow rate predictions presented in this paper are valid as the flow is stable.

Figure 16. Variations of the critical Rayleigh number $Ra_{cr}$ as functions of (a) $\alpha$ at $Re=1$, (b) $Re$ at $\alpha =2$ and (c) c at $Re=1$ and $\alpha =2$. Solid, dashed and dotted lines correspond to the transverse roll, oblique roll and travelling wave, respectively. In each plot, the minimum $Ra_{cr}$ is shown by horizontal dashed line.

8. Thermal wave applied at the upper wall

We briefly mention the situation when the thermal wave is switched from the lower to the upper wall, i.e.

(8.1a,b)\begin{equation} \theta_U (t,X) = \tfrac{1}{2} Ra_{P,U} \cos [\alpha (X-ct)], \quad \theta_L (t,X) =0 \end{equation}

where the upper wave Rayleigh number $Ra_{P,U}$ is an analogue of the (lower) wave Rayleigh number defined previously. The mechanics of the flow are akin to that seen for the thermal wave applied at the lower wall. Sample results are shown in figure 17. The similarity in the flow patterns (compare figures 5 and 17) depending on whether the wave is applied at the upper or lower wall is perhaps not surprising. Indeed, it is relatively simple to show that the governing systems for the two problems are closely related. If we take the problem of the wave at the lower wall with $Ra_{P,L}=B$ and $Ra_{P,U}=0$ and then make transformation $Ra_{P,L}\rightarrow 0$, $Ra_{P,U}\rightarrow B$, $u\rightarrow -U$, $v\rightarrow -V$, $p\rightarrow P$, $\theta \rightarrow -\varTheta$, $x \rightarrow -X+{\rm \pi}$, $y \rightarrow -Y$, we find that the underlying equations are unchanged but the thermal boundary conditions are reversed in sign. Given this relationship between the two cases, there is no need to dwell further on the case of the wave applied at the upper wall, as all the interesting properties can be inferred directly from the results of the computations when the wave is applied at the lower wall.

Figure 17. Flow topology (line) and temperature (filled colour) field at $Ra_{p,U}$=1000, with (a) $c=1$, (b) $c=10$, (c) $c=-1$, (d) $c=-10$ for $Re=1$, $\alpha =2$, $Pr=0.71$. The grey dashed lines show the meandering flow stream. Arrows show the stream flow direction.

9. Summary

The effect of thermal waves on the pressure-gradient-driven flow in a channel has been studied. The isothermal flow is characterized by the Reynolds number $Re$, and the thermal wave is characterized by its velocity $c$, wavenumber $\alpha$ and amplitude expressed in terms of the relevant Rayleigh number $Ra_{p,L}$. The waves can travel along or against the flow, thus forming cocurrent waves and countercurrent waves, respectively. The analysis assumes that the pressure gradients for the isothermal and thermal-wave modulated flows remain the same, and the effect of thermal waves is measured using the flow rate change. The increase in this flow rate demonstrates flow resistance reduction, while the decrease demonstrates a resistance increase. It is shown that all countercurrent waves and cocurrent waves with velocities smaller than the critical velocity reduce flow resistance at all Reynolds numbers $Re$ and all wavenumbers $\alpha$. Waves with velocity $-10< c<-1$, and wavenumbers in the range $1<\alpha <3$ produce the largest reduction in resistance. An increase of $Re$ beyond $Re\approx 20$ eliminates this effect for all practical purposes, and the flow behaves as an isothermal flow regardless of whether the wave is present. An increase in the wave amplitude decreases resistance proportionally to the second power of the relevant Rayleigh number for $Ra_{p,L} < \sim 2000$ when saturation effects slow down this growth.

Analysis of the mechanism governing the flow response shows that waves with velocities smaller than the critical velocity produce positive Reynolds stresses, which are responsible for the resistance reduction. However, faster waves create negative Reynolds stresses, which cause the resistance to increase. It is shown that the flow response is the same regardless of whether the wave is applied at the upper or lower walls. It is also shown that the modified flow is stable for the range of wave amplitudes being of interest in the study, i.e. for $Ra_{p,L}<\sim 2000$.