Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T03:46:41.988Z Has data issue: false hasContentIssue false
  • English
  • Français

On the problem of large-scale magnetic field generation in rotating compressible convection

Published online by Cambridge University Press:  16 April 2013

B. Favier  and
P. J. Bushby
B. Favier*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
P. J. Bushby
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon Tyne NE1 7RU, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Mean-field dynamo theory suggests that turbulent convection in a rotating layer of electrically conducting fluid produces a significant $\alpha $-effect, which is one of the key ingredients in any mean-field dynamo model. Provided that this $\alpha $-effect operates more efficiently than (turbulent) magnetic diffusion, such a system should be capable of sustaining a large-scale dynamo. However, in the Boussinesq model that was considered by Cattaneo & Hughes (J. Fluid Mech., vol. 553, 2006, pp. 401–418) the dynamo produced small-scale, intermittent magnetic fields with no significant large-scale component. In this paper, we consider the compressible analogue of the rotating convective layer that was considered by Cattaneo & Hughes (2006). Varying the horizontal scale of the computational domain, we investigate the dependence of the dynamo upon the rotation rate. Our simulations indicate that these turbulent compressible flows can drive a small-scale dynamo but, even when the layer is rotating very rapidly (with a mid-layer Taylor number of 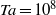$Ta= 1{0}^{8} $), we find no evidence for the generation of a significant large-scale component of the magnetic field on a dynamical time scale. Like Cattaneo & Hughes (2006), we measure a negligible (time-averaged) $\alpha $-effect when a uniform horizontal magnetic field is imposed across the computational domain. Although the total horizontal magnetic flux is a conserved quantity in these simulations, the (depth-dependent) horizontally averaged magnetic field always exhibits strong fluctuations. If these fluctuations are artificially suppressed within the code, we measure a significant mean electromotive force that is comparable to that found in related calculations in which the $\alpha $-effect is measured using the test-field method, even though we observe no large-scale dynamo action.

JFM classification

Convection: Convection MHD and Electrohydrodynamics: Dynamo theory Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 529 - 555
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A., Mininni, P. D. & Pouquet, A. 2005 Shell-to-shell energy transfer in magnetohydrodynamics. I. Steady state turbulence. Phys. Rev. E 72, 046301.CrossRefGoogle ScholarPubMed
Brandenburg, A. 2001 The inverse cascade and nonlinear alpha-effect in simulations of isotropic helical hydromagnetic turbulence. Astrophys. J. 550, 824–840.CrossRefGoogle Scholar
Brandenburg, A., Rädler, K.-H., Rheinhardt, M. & Käpylä, P. J. 2008a Magnetic diffusivity tensor and dynamo effects in rotating and shearing turbulence. Astrophys. J. 676, 740–761.CrossRefGoogle Scholar
Brandenburg, A., Rädler, K.-H. & Schrinner, M. 2008b Scale dependence of alpha effect and turbulent diffusivity. Astron. Astrophys. 482, 739–746.Google Scholar
Brummell, N. H., Clune, T. L. & Toomre, J. 2002 Penetration and overshooting in turbulent compressible convection. Astrophys. J. 570, 825–854.CrossRefGoogle Scholar
Bushby, P. J., Houghton, S. M., Proctor, M. R. E. & Weiss, N. O. 2008 Convective intensification of magnetic fields in the quiet sun. Mon. Not. R. Astron. Soc. 387, 698–706.Google Scholar
Cattaneo, F. 1999 On the origin of magnetic fields in the quiet photosphere. Astrophys. J. 515, L39–L42.Google Scholar
Cattaneo, F. & Hughes, D. W. 2006 Dynamo action in a rotating convective layer. J. Fluid Mech. 553, 401–418.CrossRefGoogle Scholar
Cattaneo, F. & Hughes, D. W. 2009 Problems with kinematic mean field electrodynamics at high magnetic Reynolds numbers. Mon. Not. R. Astron. Soc. 395, L48–L51.Google Scholar
Chan, K. L. 2007 Rotating convection in f-boxes: faster rotation. Astron. Nachr. 328, 1059–1061.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Childress, S. & Soward, A. M. 1972 Convection-driven hydromagnetic dynamo. Phys. Rev. Lett. 29, 837–839.Google Scholar
Favier, B. & Bushby, P. J. 2012 Small-scale dynamo action in rotating compressible convection. J. Fluid. Mech. 690, 262–287.CrossRefGoogle Scholar
Giesecke, A., Ziegler, U. & Rüdiger, G. 2005 Geodynamo $\alpha $ -effect derived from box simulations of rotating magnetoconvection. Phys. Earth Planet. Inter. 152, 90–102.Google Scholar
Hubbard, A. & Brandenburg, A. 2009 Memory effect in turbulent transport. Astrophys. J. 706, 712–726.Google Scholar
Hubbard, A., Sordo, F. Del, Käpylä, P. J. & Brandenburg, A. 2009 The $\alpha $ effect with imposed and dynamo-generated magnetic fields. Mon. Not. R. Astron. Soc. 398, 1891–1899.CrossRefGoogle Scholar
Hughes, D. W. & Cattaneo, F. 2008 The alpha-effect in rotating convection: size matters. J. Fluid Mech. 594, 445–461.CrossRefGoogle Scholar
Hughes, D. W. & Proctor, M. R. E. 2009 Large-scale dynamo action driven by velocity shear and rotating convection. Phys. Rev. Lett. 102, 044501.CrossRefGoogle ScholarPubMed
Hughes, D. W., Proctor, M. R. E. & Cattaneo, F. 2011 The $\alpha $ effect in rotating convection: a comparison of numerical simulations. Mon. Not. Astron. Soc. 414, L45–L49.CrossRefGoogle Scholar
Käpylä, P. J., Korpi, M. J. & Brandenburg, A. 2009a Alpha effect and turbulent diffusion from convection. Astron. Astrophys. 500, 633–646.CrossRefGoogle Scholar
Käpylä, P. J., Korpi, M. J. & Brandenburg, A. 2009b Large-scale dynamos in rigidly rotating turbulent convection. Astrophys. J. 697, 1153–1163.CrossRefGoogle Scholar
Käpylä, P. J., Korpi, M. J. & Brandenburg, A. 2010a The $\alpha $ effect in rotating convection with sinusoidal shear. Mon. Not. Astron. Soc. 402, 1458–1466.CrossRefGoogle Scholar
Käpylä, P. J., Korpi, M. J. & Brandenburg, A. 2010b Open vs closed boundaries in large-scale convective dynamos. Astron. Astrophys. 518, A22.Google Scholar
Käpylä, P. J., Mantere, M. J. & Hackman, T. 2011 Starspots due to large-scale vortices in rotating turbulent convection. Astrophys. J. 742, 34.Google Scholar
Krause, F. & Rädler, K.-H. 1980 Mean-field Magnetohydrodynamics and Dynamo Theory. Pergamon.Google Scholar
Matthews, P. C., Proctor, M. R. E. & Weiss, N. O. 1995 Compressible magnetoconvection in three dimensions: planforms and nonlinear behaviour. J. Fluid Mech. 305, 281–305.Google Scholar
Meneguzzi, M. & Pouquet, A. 1989 Turbulent dynamos driven by convection. J. Fluid Mech. 205, 297–398.CrossRefGoogle Scholar
Mitra, D., Käpylä, P. J., Tavakol, R. & Brandenburg, A. 2009 Alpha effect and diffusivity in helical turbulence with shear. Astron. Astrophys. 495, 1–8.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Moll, R., Pietarila-Graham, J. P., Pratt, J., Cameron, R. H., Müller, W.-C. & Schüssler, M. 2011 Universality of the small-scale dynamo mechanism. Astrophys. J. 736, 36.Google Scholar
Ossendrijver, M., Stix, M. & Brandenburg, A. 2001 Magnetoconvection and dynamo coefficients: dependence of the $\alpha $ effect on rotation and magnetic field. Astron. Astrophys. 376, 713–726.Google Scholar
Parker, E. N. 1955 Hydromagnetic dynamo models. Astrophys. J. 122, 293–314.Google Scholar
Pietarila-Graham, J. P., Cameron, R. H. & Schüssler, M. 2010 Turbulent small-scale dynamo action in solar surface simulations. Astrophys. J. 714, 1606–1616.CrossRefGoogle Scholar
Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M. & Christensen, U. 2005 Mean-field view on rotating magnetoconvection and a geodynamo model. Astron. Nachr. 326, 245–249.Google Scholar
Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M. & Christensen, U. 2007 Mean-field concept and direct numerical simulations of rotating magnetoconvection and the geodynamo. Geophys. Astrophys. Fluid Dyn. 101, 81–116.Google Scholar
Soward, A. M. 1974 A convection-driven dynamo: I. The weak field case. Phil. Trans. R. Soc. Lond. A 275, 611–646.Google Scholar
Steenbeck, M., Krause, F. & Rädler, K.-H. 1966 Berechnung der mittleren Lorentz–Feldstärke $ \overline{\mathbf{v} \times \mathbf{B} } $ für ein elektrisch leitendes Medium in turbulenter, durch Coriolis–Kräfte beeinflußter Bewegung. Z. Naturforsch. Teil A 21, 369–376.CrossRefGoogle Scholar
Stellmach, S. & Hansen, U. 2004 Cartesian convection-driven dynamos at low ekman number. Phys. Rev. E 70, 056312.Google Scholar
Tobias, S. M., Cattaneo, F. & Brummell, N. H. 2008 Convective dynamos with penetration, rotation and shear. Astrophys. J. 685, 596–605.Google Scholar