Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T19:44:47.733Z Has data issue: false hasContentIssue false
  • English
  • Français

On the origin of the secondary vortex street

Published online by Cambridge University Press:  24 September 2012

Bhaskar Kumar  and
Sanjay Mittal
Bhaskar Kumar
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Hyderabad, AP 502205, India
Sanjay Mittal*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, UP 208 016, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The origin of the secondary vortex street, observed in the far wake in the flow past a circular cylinder, is investigated. The Reynolds number, based on the diameter of the cylinder, is 150. The von Kármán vortex street, which originates in the near wake, decays exponentially downstream of the cylinder. Beyond the region of decay, a broad band of frequencies are selectively amplified, leading to the formation of a secondary vortex street consisting of packets of large-scale vortex structures. The streamwise location of the onset of the instability, frequency of the generation of packets and their convection speed are estimated via direct numerical simulation (DNS). Global linear stability analysis of the time-averaged flow reveals the presence of unstable convective modes that travel at almost the same speed and have a structure similar to the packet-like disturbances as observed in the DNS. Sensitivity analysis of the global convective modes to structural perturbations is carried out to locate the region of the wake that is most significant in generating the modes responsible for the appearance of the secondary vortex street. This information is utilized to control the flow. By placing a ‘slip’ splitter plate along the wake centre line, in the overlap region of the direct and the adjoint modes, the oscillations in the far wake are significantly reduced, though the oscillations related to the primary vortex shedding in the near wake are not. It is also found that suppression of the primary vortex shedding leads to annihilation of the secondary vortex street as well. Linear stability analysis of the steady-state flow does not yield any modes that can explain the appearance of the secondary vortex street. The steady and time-averaged wake profiles, for the 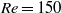flow, are compared to bring out the differences in the two. The effect of free-stream oscillations on the evolution of the secondary vortex street is investigated. By reducing the amplitude of inlet excitation, a gradual transition from ordered shedding in the far wake to the appearance of a broad-band spectrum of frequencies, as in the unforced wake, is observed. All the computations have been carried out using a stabilized finite element method.

JFM classification

Instability: Absolute/convective instability Flow Control: Instability control Wakes/Jets: Vortex streets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 711 , 25 November 2012 , pp. 641 - 666
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75, 750–756.CrossRefGoogle Scholar
2. Brooks, A. N. & Hughes, T. J. R. 1982 Streamline upwind/Petrov–Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Comput. Meth. Appl. Mech. Engng 32, 199–259.CrossRefGoogle Scholar
3. Cimbala, J. M. 1984 Large structure in the far wake of two-dimensional bluff bodies. PhD thesis, Graduate Aeronautical Laboratories, California Institute of Technology.Google Scholar
4. Cimbala, J. M., Nagib, H. M. & Roshko, A. 1988 Large structure in the far wake of two-dimensional bluff bodies. J. Fluid. Mech 190, 265–298.CrossRefGoogle Scholar
5. Durgin, W. & Karlsson, S. 1971 On the phenomenon of vortex street breakdown. J. Fluid. Mech 507–527.CrossRefGoogle Scholar
6. Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
7. Hill, D. C. 1992 A theoretical approach for analysing the restabilization of wakes. NASA Technical Memorandum 103858.CrossRefGoogle Scholar
8. Hughes, T. J. R. & Brooks, A. N. 1979 A multi-dimensional upwind scheme with no crosswind diffusion. In Finite Element Methods for Convection Dominated Flows (ed. Hughes, T. J. R. ), pp. 19–35. ASME.Google Scholar
9. Hughes, T. J. R., Franca, L. P. & Balestra, M. 1986 A new finite element formulation for computational fluid dynamics. Part 5. Circumventing the Babuška–Brezzi condition: a stable Petrov–Galerkin formulation of the Stokes problem accommodating equal-order interpolations. Comput. Meth. Appl. Mech. Engng 59, 85–99.CrossRefGoogle Scholar
10. Inoue, O. & Yamazaki, Y. 1999 Secondary vortex streets in two-dimensional cylinder wakes. Fluid Dyn. Res. 25, 1–18.CrossRefGoogle Scholar
11. Inoue, O., Yamazaki, Y. & Bisaka, T. 1995 Numerical simulation of forced wakes around a cylinder. Intl J. Heat Fluid flow 16, 327–332.CrossRefGoogle Scholar
12. Johnson, S. A., Thompson, M. C. & Hourigan, K. 2004 Predicted low frequency structures in the wake of elliptical cylinders. Eur. J. Mech. B 23, 229–239.CrossRefGoogle Scholar
13. Karasudani, T. & Funakoshi, M. 1994 Evolution of a vortex street in the far wake of a cylinder. Fluid Dyn. Res. 14, 331–352.CrossRefGoogle Scholar
14. Koopmann, G. H. 1967 The vortex wakes of vibrating cylinders at low Reynolds numbers. J. Fluid Mech. 28, 501–512.CrossRefGoogle Scholar
15. Kumar, B., Kottaram, J. J., Singh, A. K. & Mittal, S. 2009 Global stability of flow past a cylinder with centreline symmetry. J. Fluid Mech. 632, 273–300.CrossRefGoogle Scholar
16. Kumar, B. & Mittal, S. 2003 Flow past a rotating cylinder. J. Fluid. Mech 476, 303–334.Google Scholar
17. Kumar, B. & Mittal, S. 2006 Prediction of critical Reynolds number for the flow past a circular cylinder. Comput. Meth. Appl. Mech. Engng 195, 6046–6058.CrossRefGoogle Scholar
18. Kumar, B. & Mittal, S. 2009 Convectively unstable anti-symmetric waves in flows past bluff bodies. Comput. Model. Engng Sci. 53, 95–122.Google Scholar
19. Liu, C., Zheng, X. & Sung, C. H. 1998 Preconditioned multigrid methods for unsteady incompressible flows. J. Comput. Phys. 139, 35–57.CrossRefGoogle Scholar
20. Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
21. Matsui, T. & Okude, M. 1981 Vortex pairing in a Karman vortex street. In Proceedings of the Seventh Biennial Symposium on Turbulence, Rolla, Missouri.Google Scholar
22. Matsui, T. & Okude, M. 1982 Formation of the secondary vortex street in the wake of a circular cylinder. IUTAM Symposium, Marseilles.CrossRefGoogle Scholar
23. Mittal, S. 2000 On the performance of high aspect ratio elements for incompressible flows. Comput. Meth. Appl. Mech. Engng 188, 269–287.CrossRefGoogle Scholar
24. Mittal, S. 2003 Effect of a ‘slip’ splitter plate on vortex shedding from a cylinder. Phys. Fluids 15, 817–820.CrossRefGoogle Scholar
25. Mittal, S. 2008a Global linear stability analysis of time-averaged flows. Intl J. Numer. Meth. Fluids 58, 111–118.CrossRefGoogle Scholar
26. Mittal, S. 2008b Linear stability analysis of time-averaged flow past a cylinder. Comput. Model. Engng Sci. 27, 63–78.Google Scholar
27. Mittal, S. 2009 Onset of mixing layer instability in flow past a plate. Intl J. Numer. Meth. Fluids 59, 1035–1049.CrossRefGoogle Scholar
28. Mittal, S., Kottaram, J. J. & Kumar, B. 2008 Onset of shear layer instability in flow past a cylinder. Phys. Fluids 20, 054102.CrossRefGoogle Scholar
29. Mittal, S. & Kumar, B. 2007 A stabilized finite element method for global analysis of convective instabilities in nonparallel flows. Phys. Fluids 19, 088105.CrossRefGoogle Scholar
30. Najjar, F. M. & Balachandar, S. 1998 Low-frequency unsteadiness in the wake of a normal flat plate. J. Fluid Mech. 370, 101–147.CrossRefGoogle Scholar
31. Pier, B. & Huerre, P. 2001 Nonlinear self-sustained structures and fronts in spatially developing wake flows. J. Fluid Mech. 435, 145–174.CrossRefGoogle Scholar
32. Sato, H. & Kuriki, K. 1961 The mechanism of transition in the wake of a thin flat plate placed parallel to a uniform flow. J. Fluid Mech. 11, 321–352.CrossRefGoogle Scholar
33. Stewart, G. W. 1975 Methods of simultaneous iteration for calculating eigenvectors of matrices. In Topics in Numerical Analysis II (ed. Miller, J. H. H. ), pp. 169–185. Academic.Google Scholar
34. Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
35. Taneda, S. 1959 Downstream development of wakes behind cylinders. J. Phys. Soc. Japan 843–848.CrossRefGoogle Scholar
36. Tezduyar, T. E., Mittal, S., Ray, S. E. & Shih, R. 1992 Incompressible flow computations with stabilized bilinear and linear equal-order-interpolation velocity–pressure elements. Comput. Meth. Appl. Mech. Engng 95, 221–242.CrossRefGoogle Scholar
37. Triantafyllou, G. S. & Karniadakis, G. 1990 Computational reducibility of unsteady viscous flows. Phys. Fluids 2, 653–656.CrossRefGoogle Scholar
38. Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.CrossRefGoogle Scholar
39. Williamson, C. H. K. & Prasad, A. 1993a A new mechanism for oblique wave resonance in the ‘natural’ far wake. J. Fluid. Mech 256, 269–313.CrossRefGoogle Scholar
40. Williamson, C. H. K. & Prasad, A. 1993b Acoustic forcing of oblique wave resonance in the far wake. J. Fluid. Mech 256, 315–341.CrossRefGoogle Scholar
41. Zhang, H., Fey, U., Noack, B. R., Konig, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7, 779–794.CrossRefGoogle Scholar