Article contents
On the nature of fluctuations in turbulent Rayleigh–Bénard convection at large Prandtl numbers
Published online by Cambridge University Press: 03 August 2016
Abstract
We report experimental results for the power spectra, variance, skewness and kurtosis of temperature fluctuations in turbulent Rayleigh–Bénard convection (RBC) of a fluid with Prandtl number 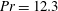 $Pr=12.3$ in cylindrical samples with aspect ratios
$Pr=12.3$ in cylindrical samples with aspect ratios 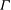 $\unicode[STIX]{x1D6E4}$ (diameter
$\unicode[STIX]{x1D6E4}$ (diameter 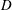 $D$ over height
$D$ over height 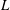 $L$) of 0.50 and 1.00. The measurements were primarily for the radial positions
$L$) of 0.50 and 1.00. The measurements were primarily for the radial positions 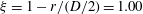 $\unicode[STIX]{x1D709}=1-r/(D/2)=1.00$ and
$\unicode[STIX]{x1D709}=1-r/(D/2)=1.00$ and 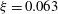 $\unicode[STIX]{x1D709}=0.063$. In both cases, data were obtained at several vertical locations
$\unicode[STIX]{x1D709}=0.063$. In both cases, data were obtained at several vertical locations 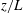 $z/L$. For all locations, there is a frequency range of about a decade over which the spectra can be described well by the power law
$z/L$. For all locations, there is a frequency range of about a decade over which the spectra can be described well by the power law 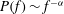 $P(f)\sim f^{-\unicode[STIX]{x1D6FC}}$. For all
$P(f)\sim f^{-\unicode[STIX]{x1D6FC}}$. For all 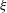 $\unicode[STIX]{x1D709}$ and
$\unicode[STIX]{x1D709}$ and 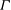 $\unicode[STIX]{x1D6E4}$, the
$\unicode[STIX]{x1D6E4}$, the  $\unicode[STIX]{x1D6FC}$ value is less than one near the top and bottom plates and increases as
$\unicode[STIX]{x1D6FC}$ value is less than one near the top and bottom plates and increases as 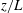 $z/L$ or
$z/L$ or 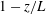 $1-z/L$ increase from 0.01 to 0.5. This differs from the finding for
$1-z/L$ increase from 0.01 to 0.5. This differs from the finding for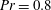 $Pr=0.8$ (He et al., Phys. Rev. Lett., vol. 112, 2014, 174501) and the expectation for the downstream velocity of turbulent wall-bounded shear flow (Rosenberg, J. Fluid Mech., vol. 731, 2013, pp. 46–63), where
$Pr=0.8$ (He et al., Phys. Rev. Lett., vol. 112, 2014, 174501) and the expectation for the downstream velocity of turbulent wall-bounded shear flow (Rosenberg, J. Fluid Mech., vol. 731, 2013, pp. 46–63), where 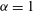 $\unicode[STIX]{x1D6FC}=1$ is found or expected in an inner layer (
$\unicode[STIX]{x1D6FC}=1$ is found or expected in an inner layer (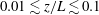 $0.01\lesssim z/L\lesssim 0.1$) near the wall but in the bulk. The variance is described better by a power law
$0.01\lesssim z/L\lesssim 0.1$) near the wall but in the bulk. The variance is described better by a power law 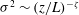 $\unicode[STIX]{x1D70E}^{2}\sim (z/L)^{-\unicode[STIX]{x1D701}}$ than by the logarithmic dependence found or expected for
$\unicode[STIX]{x1D70E}^{2}\sim (z/L)^{-\unicode[STIX]{x1D701}}$ than by the logarithmic dependence found or expected for 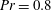 $Pr=0.8$ and for turbulent shear flow. For both
$Pr=0.8$ and for turbulent shear flow. For both 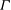 $\unicode[STIX]{x1D6E4}$, we found that, independent of Rayleigh number,
$\unicode[STIX]{x1D6E4}$, we found that, independent of Rayleigh number, 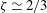 $\unicode[STIX]{x1D701}\simeq 2/3$ near the sidewall (
$\unicode[STIX]{x1D701}\simeq 2/3$ near the sidewall (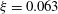 $\unicode[STIX]{x1D709}=0.063$), where plumes primarily rise or fall and the large-scale circulation (LSC) dynamics is most influential. This result agrees with a model due to Priestley (Turbulent Transfer in the Lower Atmosphere, 1959, University of Chicago Press) for convection over a horizontal heated surface. However, we found
$\unicode[STIX]{x1D709}=0.063$), where plumes primarily rise or fall and the large-scale circulation (LSC) dynamics is most influential. This result agrees with a model due to Priestley (Turbulent Transfer in the Lower Atmosphere, 1959, University of Chicago Press) for convection over a horizontal heated surface. However, we found 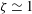 $\unicode[STIX]{x1D701}\simeq 1$ along the sample centreline (
$\unicode[STIX]{x1D701}\simeq 1$ along the sample centreline (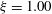 $\unicode[STIX]{x1D709}=1.00$), where there are relatively few plumes moving vertically and the LSC dynamics is expected to be less important; that result is consistent with one of two possible interpretations by Adrian (Intl J. Heat Mass Transfer, vol. 39, 1996, pp. 2303–2310) of a model due to Libchaber et al. (J. Fluid Mech., vol. 204, 1989, pp. 1–30). We discuss the composite nature of fluctuations in turbulent RBC, with contributions from intrinsic background fluctuations, plumes, the stochastic dynamics of the LSC, and the sloshing and torsional mode of the LSC. None of the models advanced so far explicitly consider all of these contributions.
$\unicode[STIX]{x1D709}=1.00$), where there are relatively few plumes moving vertically and the LSC dynamics is expected to be less important; that result is consistent with one of two possible interpretations by Adrian (Intl J. Heat Mass Transfer, vol. 39, 1996, pp. 2303–2310) of a model due to Libchaber et al. (J. Fluid Mech., vol. 204, 1989, pp. 1–30). We discuss the composite nature of fluctuations in turbulent RBC, with contributions from intrinsic background fluctuations, plumes, the stochastic dynamics of the LSC, and the sloshing and torsional mode of the LSC. None of the models advanced so far explicitly consider all of these contributions.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 18
- Cited by



