Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T04:28:58.621Z Has data issue: false hasContentIssue false
  • English
  • Français

On the length scales of hypersonic shock-induced large separation bubbles near leading edges

Published online by Cambridge University Press:  30 September 2016

R. Sriram ,
L. Srinath ,
Manoj Kumar K. Devaraj  and
G. Jagadeesh
R. Sriram
Affiliation:
Laboratory for Hypersonic and Shock wave Research, Department of Aerospace Engineering, Indian Institute of Science, Bangalore, 560012, India
L. Srinath
Affiliation:
Laboratory for Hypersonic and Shock wave Research, Department of Aerospace Engineering, Indian Institute of Science, Bangalore, 560012, India
Manoj Kumar K. Devaraj
Affiliation:
Center of Excellence in Hypersonics, Indian Institute of Science, Bangalore, 560012, India
G. Jagadeesh*
Affiliation:
Laboratory for Hypersonic and Shock wave Research, Department of Aerospace Engineering, Indian Institute of Science, Bangalore, 560012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The interaction of a hypersonic boundary layer on a flat plate with an impinging shock – an order of magnitude stronger than that required for incipient separation of the boundary layer – near sharp and blunt leading edges (with different bluntness radii from 2 to 6 mm) is investigated experimentally, complemented by numerical computations. The resultant separation bubble is of length comparable to the distance of shock impingement from the leading edge, rather than the boundary layer thickness at separation; it is termed large separation bubble. 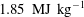Experiments are performed in the IISc hypersonic shock tunnel HST-2 at nominal Mach numbers 5.88 and 8.54, with total enthalpies 1.26 and $1.85~\text{MJ}~\text{kg}^{-1}$ respectively. Schlieren flow visualization using a high-speed camera and surface pressure measurements using fast response sensors are the diagnostics. For the sharp leading edge case, the separation length was found to follow an inviscid scaling law according to which the scaled separation length 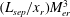$(L_{sep}/x_{r})M_{er}^{3}$ is found to be linearly related to the reattachment pressure ratio $p_{r}/p_{er}$; where 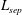$L_{sep}$ is the measured separation length, 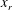$x_{r}$ the distance of reattachment from the leading edge, 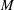$M$ the Mach number, 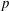$p$ the static pressure and the subscripts $r$ and $e$ denote the conditions at the reattachment location and at the edge of the boundary layer at the shock impingement location respectively. However, for all the blunt leading edges 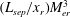$(L_{sep}/x_{r})M_{er}^{3}$ was found to be a constant irrespective of Mach number and much smaller than the sharp leading edge cases. The possible contributions of viscous and non-viscous mechanisms towards the observed phenomena are explored.

JFM classification

Boundary Layers: Boundary layer separation Compressible Flows: Gas dynamics Aerodynamics: High-speed flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 806 , 10 November 2016 , pp. 304 - 355
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Marie Curie Fellow in Aerospace Engineering (Aerospace Sciences), School of Engineering, University of Glasgow, Glasgow G12 8QQ, UK.

References

Anderson, J. D. 1989 Hypersonic and High Temperature Gas Dynamics. McGraw-Hill.Google Scholar
Ball, K. O. W. 1971 Flap span effects on boundary-layer separation. AIAA J. 9 (10), 2080–2081.CrossRefGoogle Scholar
Billig, F. S. 1967 Shock-wave shapes around spherical-and cylindrical-nosed bodies. J. Spacecr. Rockets 4 (6), 822–823.Google Scholar
Bleilebens, M. & Olivier, H. 2006 On the influence of elevated surface temperatures on hypersonic shock wave/boundary layer interaction at a heated ramp model. Shock Waves 15 (5), 301–312.Google Scholar
Borovoi, V. Y., Egorov, I. V., Skuratov, A. S. & Struminskaya, I. V. 2005 Interaction between an inclined shock and boundary and high-entropy layers on a flat plate. Fluid Dyn. 40 (6), 911–928.Google Scholar
Borovoy, V. Y., Egorov, I. V., Skuratov, A. S. & Struminskaya, I. V. 2012 Two-dimensional shock-wave/boundary-layer interaction in the presence of entropy layer. AIAA J. 51 (1), 80–93.CrossRefGoogle Scholar
Chapman, D. R., Kuehn, D. M. & Larson, H. K.1957 Investigation of separated flows in supersonic and subsonic streams with emphasis on the effect of transition. NACA Tech. Rep. TN-3869.Google Scholar
Chen, X.-q., Hou, Z.-x., Liu, J.-x. & Gao, X.-z. 2011 Bluntness impact on performance of waverider. Comput. Fluids 48 (1), 30–43.CrossRefGoogle Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.Google Scholar
Coleman, G. T. & Stollery, J. L. 1972 Heat transfer from hypersonic turbulent flow at a wedge compression corner. J. Fluid Mech. 56 (04), 741–752.Google Scholar
Creager, M. O.1957 Effects of leading-edge blunting on the local heat transfer and pressure distributions over flat plates in supersonic flow. NACA Tech. Rep. TN 4142.Google Scholar
Davies, W. R. & Bernstein, L. 1969 Heat transfer and transition to turbulence in the shock-induced boundary layer on a semi-infinite flat plate. J. Fluid Mech. 36 (01), 87–112.CrossRefGoogle Scholar
Davis, J. P. & Sturtevant, B. 2000 Separation length in high-enthalpy shock/boundary-layer interaction. Phys. Fluids 12 (10), 2661–2687.CrossRefGoogle Scholar
Delery, J. & Coet, M. C. 1991 Experiments on shock-wave/boundary-layer interactions produced by two-dimensional ramps and three-dimensional obstacles. In Hypersonic Flows for Reentry Problems, pp. 97–128. Springer.Google Scholar
Délery, J. & Dussauge, J. 2009 Some physical aspects of shock wave/boundary layer interactions. Shock Waves 19 (6), 453–468.CrossRefGoogle Scholar
Délery, J. & Marvin, J. G.1986 Shock-wave boundary layer interactions. Tech. Rep. AGARD-AG-280.Google Scholar
Eckert, E. R. G. 1955 Engineering relations for friction and heat transfer to surfaces in high velocity flow. J. Aero. Sci. 22 (8), 585–587.Google Scholar
Elfstrom, G. M. 1972 Turbulent hypersonic flow at a wedge-compression corner. J. Fluid Mech. 53 (1), 113–129.Google Scholar
Erdem, E., Kontis, K., Johnstone, E., Murray, N. P. & Steelant, J. 2013 Experiments on transitional shock wave–boundary layer interactions at mach 5. Exp. Fluids 54 (10), 1–22.Google Scholar
Fay, J. F. & Sambamurthi, J.1992 Laminar hypersonic flow over a compression corner using the hana code. AIAA Paper 92-2896.CrossRefGoogle Scholar
Gadd, G. E., Holder, D. W. & Regan, J. D. 1954 An experimental investigation of the interaction between shock waves and boundary layers. Proc. R. Soc. Lond. A 226, 227–253.Google Scholar
Hayakawa, K. & Squire, L. C. 1982 The effect of the upstream boundary-layer state on the shock interaction at a compression corner. J. Fluid Mech. 122, 369–394.Google Scholar
Holden, M. S. 1970 Boundary-layer displacement and leading-edge bluntness effects on attached and separated laminar boundary layers in a compression corner. I-theoretical study. AIAA J. 8, 2179–2188.CrossRefGoogle Scholar
Holden, M. S. 1971a Boundary-layer displacement and leading-edge bluntness effects on attached and separated laminar boundary layers in a compression corner. II-experimental study. AIAA J. 9 (1), 84–93.Google Scholar
Holden, M. S. 1971b Establishment time of laminar separated flows. AIAA J. 9 (11), 2296–2298.Google Scholar
Humble, R. A., Elsinga, G. E., Scarano, F. & Van Oudheusden, B. W. 2009 Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 622, 33–62.Google Scholar
John, B. & Kulkarni, V. 2014 Effect of leading edge bluntness on the interaction of ramp induced shock wave with laminar boundary layer at hypersonic speed Comput. Fluids 96, 177–190.Google Scholar
Katzer, E. 1989 On the lengthscales of laminar shock/boundary-layer interaction. J. Fluid Mech. 206, 477–496.Google Scholar
Krek, R. M. & Jacobs, P. A.1993 Stn, shock tube and nozzle calculations for equilibrium air. Tech. Rep. Research Report No. 2/93, The University of Queensland.Google Scholar
Krishnan, L., Yao, Y., Sandham, N. D. & Roberts, G. T. 2005 On the response of shock-induced separation bubble to small amplitude disturbances. Mod. Phys. Lett. B 19, 1495–1498.Google Scholar
Lewis, J. E., Kubota, T. & Lees, L. 1968 Experimental investigation of supersonic laminar, two-dimensional boundary-layer separation in a compression corner with and without cooling. AIAA J. 6 (1), 7–14.Google Scholar
Mallinson, S. G., Gai, S. L. & Mudford, N. R. 1996a High-enthalpy, hypersonic compression corner flow. AIAA J. 34 (6), 1130–1137.Google Scholar
Mallinson, S. G., Gai, S. L. & Mudford, N. R. 1996b Leading-edge bluntness effects in high enthalpy, hypersonic compression corner flow. AIAA J. 34 (11), 2284–2290.Google Scholar
Mallinson, S. G., Gai, S. L. & Mudford, N. R. 1997a Establishment of steady separated flow over a compression–corner in a free–piston shock tunnel. Shock Waves 7 (4), 249–253.CrossRefGoogle Scholar
Mallinson, S. G., Gai, S. L. & Mudford, N. R. 1997b The interaction of a shock wave with a laminar boundary layer at a compression corner in high-enthalpy flows including real gas effects. J. Fluid Mech. 342, 1–35.Google Scholar
Miller, D. S., Hijman, R. & Childs, M. E. 1964 Mach 8 to 22 studies of flow separations due to deflected control surfaces. AIAA J. 2 (2), 312–321.Google Scholar
Moffat, R. J. 1988 Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1 (1), 3–17.Google Scholar
Munikrishna, N.2007 On viscous flux discretization procedures for finite volume and meshless solvers. PhD thesis, Indian Institute of Science.Google Scholar
Murray, N., Hillier, R. & Williams, S. 2013 Experimental investigation of axisymmetric hypersonic shock-wave/turbulent-boundary-layer interactions. J. Fluid Mech. 714, 152–189.CrossRefGoogle Scholar
Needham, D. A.1965 Laminar separation in hypersonic flow. PhD thesis, Imperial College London.Google Scholar
Needham, D. A. & Stollery, J. L.1966 Boundary layer separation in hypersonic flow. AIAA Paper 66-455.Google Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at m = 2. 25. Phys. Fluids 18 (6), 065113.Google Scholar
Rudman, S. & Rubin, S. G. 1968 Hypersonic viscous flow over slender bodies with sharp leading edges. AIAA J. 6 (10), 1883–1890.CrossRefGoogle Scholar
Schetz, J. A. & Fuhs, A. E. 1921 Handbook of Fluid Dynamics and Fluid Machinery. John Wiley and Sons.Google Scholar
Settles, G. S. & Bogdonoff, S. M. 1982 Scaling of two- and three-dimensional shock/turbulent boundary-layer interactions at compression corners. AIAA J. 20 (6), 782–789.Google Scholar
Shende, N. & Balakrishnan, N. 2004 New migratory memory algorithm for implicit finite volume solvers. AIAA J. 42 (9), 1863–1870.Google Scholar
Spaid, F. W. & Frishett, J. C. 1972 Incipient separation of a supersonic, turbulent boundary layer, including effects of heat transfer. AIAA J. 10 (7), 915–922.Google Scholar
Srinivasan, S., Tannehill, J. C. & Weilmuenster, K. J.1986 Simplified curve fits for the thermodynamic properties of equilibrium air. NASA Tech. Rep. Report No. 1181.Google Scholar
Sriram, R.2013 Shock tunnel investigations on hypersonic impinging boundary layer interaction. PhD thesis, Indian Institute of Science.Google Scholar
Sriram, R. & Jagadeesh, G. 2014 Shock tunnel experiments on control of shock induced large separation bubble using boundary layer bleed. Aerosp. Sci. Technol. 36, 87–93.CrossRefGoogle Scholar
Sriram, R. & Jagadeesh, G. 2015a Correlation for length of impinging shock-induced large separation bubble at hypersonic speed. AIAA J. 53 (9), 2771–2776.Google Scholar
Sriram, R., Ram, S. N., Hegde, G. M., Nayak, M. M. & Jagadeesh, G. 2015b Shock tunnel measurements of surface pressures in shock induced separated flow field using mems sensor array. Meas. Sci. Technol. 26 (9), 095301.Google Scholar
Stewartson, K. & Williams, P. G. 1969 Self-induced separation. Proc. R. Soc. Lond. A 312, 181–206.Google Scholar
Swantek, A. B. & Austin, J. M. 2015 Flowfield establishment in hypervelocity shock-wave/boundary-layer interactions. AIAA J. 53 (2), 311–320.Google Scholar
Toro, E. F., Spruce, M. & Speares, W. 1994 Restoration of the contact surface in the hll-riemann solver. Shock Waves 4 (1), 25–34.Google Scholar
Venkatakrishnan, V. 1995 Convergence to steady state solutions of the euler equations on unstructured grids with limiters. J. Comput. Phys. 118 (1), 120–130.CrossRefGoogle Scholar
Verma, S. B. & Manisankar, C. 2012 Shockwave/boundary-layer interaction control on a compression ramp using steady micro jets. AIAA J. 50 (12), 2753–2764.CrossRefGoogle Scholar