1. Introduction
Internal gravity waves (IGWs) propagate in stably stratified fluids. They are the consequence of a restoring buoyancy force that makes fluid particles oscillate around their floatability level. Internal gravity waves can be found in various environments, including the atmosphere, oceans, lakes, rivers and industrial flows (Lelong & Riley Reference Lelong and Riley1991; Staquet & Sommeria Reference Staquet and Sommeria2002). They can be excited by wind shear, buoyancy forcing due to heating, topography or tides (Vallis Reference Vallis2017). They are important because they transport mass, momentum and energy, which can significantly impact the large-scale features of stratified flows. The mutual nonlinear interactions between IGWs and with other flow components can lead to the transfer of energy between different scales. This results in the generation of smaller-scale waves and vortices.
Internal gravity waves have been studied from a variety of perspectives, including observations (MacKinnon et al. Reference MacKinnon, Alford, Sun, Pinkel, Zhao and Klymak2013), experiments (Rodda et al. Reference Rodda, Savaro, Davis, Reneuve, Augier, Sommeria, Valran, Viboud and Mordant2022; Lanchon et al. Reference Lanchon, Mora, Monsalve and Cortet2023), numerical simulations (Pan et al. Reference Pan, Arbic, Nelson, Menemenlis, Peltier, Xu and Li2020; Lam, Delache & Godeferd Reference Lam, Delache and Godeferd2021) and theoretical models (Caillol & Zeitlin Reference Caillol and Zeitlin2000; Lvov & Tabak Reference Lvov and Tabak2001; Dematteis & Lvov Reference Dematteis and Lvov2021). Under the Boussinesq approximation, three key non-dimensional numbers drive stratified flows. Namely, the Froude number ![]() $Fr = U/(NL)$, the Reynolds number
$Fr = U/(NL)$, the Reynolds number ![]() $Re =UL/\nu$ and the Prandtl number
$Re =UL/\nu$ and the Prandtl number ![]() $Pr=\nu /\kappa$, where
$Pr=\nu /\kappa$, where ![]() $U$ is the typical velocity of the flow,
$U$ is the typical velocity of the flow, ![]() $L$ the size of the domain,
$L$ the size of the domain, ![]() $N$ the Brunt–Väisälä frequency,
$N$ the Brunt–Väisälä frequency, ![]() $\nu$ is the viscosity and
$\nu$ is the viscosity and ![]() $\kappa$ is the scalar diffusivity. When the flow is composed of waves only, being strongly stratified (i.e.
$\kappa$ is the scalar diffusivity. When the flow is composed of waves only, being strongly stratified (i.e. ![]() $Fr \ll 1$), with the viscosity and diffusivity being small (i.e.
$Fr \ll 1$), with the viscosity and diffusivity being small (i.e. ![]() $Re , Pr Re \gg 1$) but such that the dynamics of energetic modes remains weakly nonlinear, a regime described by the weak wave turbulence (WWT) theory is foreseen (Hasselmann Reference Hasselmann1966; Zakharov, L'vov & Falkovich Reference Zakharov, L'vov and Falkovich1992; Nazarenko Reference Nazarenko2011; Galtier Reference Galtier2022). In such a state, the energy is concentrated on the linear dispersion relation for a continuum range of scales, as observed in the numerical simulations of Le Reun, Favier & Le Bars (Reference Le Reun, Favier and Le Bars2018). It is characterized by interactions over wave triads satisfying resonance conditions in wave vectors and frequencies. Note that, in this theoretical description, we do not consider a shear flow and vortical modes (with vorticity parallel to the vertical axis), so the typical velocity
$Re , Pr Re \gg 1$) but such that the dynamics of energetic modes remains weakly nonlinear, a regime described by the weak wave turbulence (WWT) theory is foreseen (Hasselmann Reference Hasselmann1966; Zakharov, L'vov & Falkovich Reference Zakharov, L'vov and Falkovich1992; Nazarenko Reference Nazarenko2011; Galtier Reference Galtier2022). In such a state, the energy is concentrated on the linear dispersion relation for a continuum range of scales, as observed in the numerical simulations of Le Reun, Favier & Le Bars (Reference Le Reun, Favier and Le Bars2018). It is characterized by interactions over wave triads satisfying resonance conditions in wave vectors and frequencies. Note that, in this theoretical description, we do not consider a shear flow and vortical modes (with vorticity parallel to the vertical axis), so the typical velocity ![]() $U$ corresponds to velocity fluctuations of weakly nonlinear waves and not to a mean flow velocity.
$U$ corresponds to velocity fluctuations of weakly nonlinear waves and not to a mean flow velocity.
The WWT theory for geophysical flows was developed notably in the 1960s by Hasselmann (Reference Hasselmann1966), who derived a general kinetic equation using a Lagrangian formalism for several wave systems (Hasselmann Reference Hasselmann1967), including IGWs. Müller & Olbers (Reference Müller and Olbers1975); Olbers (Reference Olbers1976) extended the work of Hasselmann to write the first kinetic equation for internal waves, i.e. with rotation and stratification. Since then, the kinetic equation for internal waves, with or without rotation and in or outside the hydrostatic limit, has been re-derived using various approaches: Clebsch variables (Pelinovsky & Raevsky Reference Pelinovsky and Raevsky1977; Voronovich Reference Voronovich1979); a decomposition between vertical velocity, the potential part of the horizontal velocity and vertical vorticity (Caillol & Zeitlin Reference Caillol and Zeitlin2000, Reference Caillol and Zeitlin2001); and isopycnal coordinates (Lvov & Tabak Reference Lvov and Tabak2001, Reference Lvov and Tabak2004; Medvedev & Zeitlin Reference Medvedev and Zeitlin2007). We refer the reader to Lvov, Polzin & Yokoyama (Reference Lvov, Polzin and Yokoyama2012) for a review of earlier IGW kinetic equations. Three classes of triadic interactions corresponding to non-local transfers were identified (McComas & Bretherton Reference McComas and Bretherton1977). Induced diffusion (ID) occurs when one low-frequency wave interacts with two approximately identical waves of much larger wavenumber and frequency. Elastic scattering occurs when two waves which are nearly vertical reflections of each other interact with a third wave which has a low frequency and almost twice the vertical wavenumber of the other two waves. Finally, the parametric subharmonic instability mechanism is an instability wherein a low wavenumber wave decays into two high wave-vector waves of half its frequency. Recently, it has been found that local interactions, i.e. involving waves with similar wave-vector amplitudes, are also very important in the energy transfers (Dematteis & Lvov Reference Dematteis and Lvov2021; Wu & Pan Reference Wu and Pan2023), particularly those which lie on the same vertical plane.
Weak wave turbulence gives predictions, among other things, for the wave energy spectrum ![]() $e_{\boldsymbol {k}}$. Usually, the theory is formulated in terms of the wave-action spectrum
$e_{\boldsymbol {k}}$. Usually, the theory is formulated in terms of the wave-action spectrum ![]() $n_{\boldsymbol {k}} = e_{\boldsymbol {k}} / \omega _{\boldsymbol {k}}$, with
$n_{\boldsymbol {k}} = e_{\boldsymbol {k}} / \omega _{\boldsymbol {k}}$, with ![]() $\omega _{\boldsymbol {k}}$ being the wave frequency. Physically,
$\omega _{\boldsymbol {k}}$ being the wave frequency. Physically, ![]() $n_{\boldsymbol {k}}$ is interpreted as the number of waves with wave vector
$n_{\boldsymbol {k}}$ is interpreted as the number of waves with wave vector ![]() $\boldsymbol {k}$. The theory gives the kinetic equation
$\boldsymbol {k}$. The theory gives the kinetic equation ![]() $\dot {n}_{\boldsymbol {k}} = St_{\boldsymbol {k}}$,
$\dot {n}_{\boldsymbol {k}} = St_{\boldsymbol {k}}$, ![]() $St_{\boldsymbol {k}}$ being the collision integral, describing the dynamics of the wave-action spectrum on a long time scale due to wave–wave interactions. In particular, axisymmetric, bihomogeneous, steady-state wave-action spectra
$St_{\boldsymbol {k}}$ being the collision integral, describing the dynamics of the wave-action spectrum on a long time scale due to wave–wave interactions. In particular, axisymmetric, bihomogeneous, steady-state wave-action spectra ![]() $n_{\boldsymbol {k}} \propto k_h^{\nu _h} |k_z|^{\nu _z}$ were previously obtained as solutions of the kinetic equation in the hydrostatic limit. They correspond to the zeros of the collision integral, including the thermal equilibrium spectrum (often called the Rayleigh–Jeans (RJ) spectrum) or spectra associated with a non-zero energy flux (called Kolmogorov–Zakharov (KZ) spectra). Using energy conservation, one KZ spectrum was found analytically
$n_{\boldsymbol {k}} \propto k_h^{\nu _h} |k_z|^{\nu _z}$ were previously obtained as solutions of the kinetic equation in the hydrostatic limit. They correspond to the zeros of the collision integral, including the thermal equilibrium spectrum (often called the Rayleigh–Jeans (RJ) spectrum) or spectra associated with a non-zero energy flux (called Kolmogorov–Zakharov (KZ) spectra). Using energy conservation, one KZ spectrum was found analytically ![]() $n_{\boldsymbol {k}} \propto k_h^{-7/2} |k_z|^{-1/2}$. It is known as the Pelinovsky–Raevsky (PR) spectrum (Pelinovsky & Raevsky Reference Pelinovsky and Raevsky1977; Caillol & Zeitlin Reference Caillol and Zeitlin2000; Lvov & Tabak Reference Lvov and Tabak2001). However, as we will explain in § 3.4, it has been found that this spectrum is not a mathematically valid solution (Caillol & Zeitlin Reference Caillol and Zeitlin2000; Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010), and is thus physically irrelevant. Using numerical integration,
$n_{\boldsymbol {k}} \propto k_h^{-7/2} |k_z|^{-1/2}$. It is known as the Pelinovsky–Raevsky (PR) spectrum (Pelinovsky & Raevsky Reference Pelinovsky and Raevsky1977; Caillol & Zeitlin Reference Caillol and Zeitlin2000; Lvov & Tabak Reference Lvov and Tabak2001). However, as we will explain in § 3.4, it has been found that this spectrum is not a mathematically valid solution (Caillol & Zeitlin Reference Caillol and Zeitlin2000; Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010), and is thus physically irrelevant. Using numerical integration, ![]() $n_{\boldsymbol {k}}\propto k_h^{-3.69}$ actually turned out to be the only zero of the collision integral (Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021). More recently, Lanchon & Cortet (Reference Lanchon and Cortet2023) derived a stationary solution (
$n_{\boldsymbol {k}}\propto k_h^{-3.69}$ actually turned out to be the only zero of the collision integral (Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021). More recently, Lanchon & Cortet (Reference Lanchon and Cortet2023) derived a stationary solution (![]() $n_{\boldsymbol {k}}\propto k_h^{-3} |k_z|^{-1}$) of a simplified kinetic equation describing the small scales of the non-local internal wave turbulence problem. This derivation is based on the assumption that energy transfers are driven only by ID triads, which lead to a scale separation in the kinetic equation.
$n_{\boldsymbol {k}}\propto k_h^{-3} |k_z|^{-1}$) of a simplified kinetic equation describing the small scales of the non-local internal wave turbulence problem. This derivation is based on the assumption that energy transfers are driven only by ID triads, which lead to a scale separation in the kinetic equation.
As said earlier, there are already four ways of deriving the kinetic equation of IGW. The Lagrangian approach (Hasselmann Reference Hasselmann1967; Olbers Reference Olbers1976) has the advantage of being non-hydrostatic and takes into account rotation. Yet, the incompressibility has to be treated perturbatively and some computations could be simplified by exploiting Hermitian symmetries. Furthermore, even if it is not the purpose of the present study, the Lagrangian formalism is not adapted if we want to include vertical vorticity (or geostrophic modes when rotation is added) (Caillol & Zeitlin Reference Caillol and Zeitlin2000). The approaches using Clebsch variables (Pelinovsky & Raevsky Reference Pelinovsky and Raevsky1977; Voronovich Reference Voronovich1979) have the advantage of being Hamiltonian. However, the decomposition does not apply to fields with vertical vorticity, the physical meaning of the conjugate variables is less straightforward, and the references are not easily available. The isopycnal coordinates (Lvov & Tabak Reference Lvov and Tabak2001; Lvov, Polzin & Tabak Reference Lvov, Polzin and Tabak2004; Medvedev & Zeitlin Reference Medvedev and Zeitlin2007) have the advantages of being a canonical Hamiltonian description of the flow and being able to take into account vertical vorticity (or geostrophic modes), but only in the hydrostatic limit. Milder (Reference Milder1982) gave a Hamiltonian description of the flow holding outside the hydrostatic limit, but it is not canonical and the kinetic equation of IGW was not derived. The decomposition used by Caillol & Zeitlin (Reference Caillol and Zeitlin2000) is the closest in spirit to the present study. It has the advantage of being derived in the very common Eulerian coordinates system, to allow the description of vortical modes, and to be valid outside the hydrostatic limit. Yet, the resulting kinetic equation was not shown to have a canonical structure. We show here that it turns out to be the case (after accounting for misprints which were corrected in an Erratum Caillol & Zeitlin Reference Caillol and Zeitlin2001). Here, we use the poloidal–toroidal decomposition (Godeferd, Delache & Cambon Reference Godeferd, Delache and Cambon2010), also known as the Craya–Herring decomposition (Craya Reference Craya1957; Herring Reference Herring1974). As explained later, it is particularly adapted to the derivation of the kinetic equation of IGWs. Namely, it uses the common Eulerian coordinates system, offers a complete basis of the components of stratified flows and takes into account incompressibility from the beginning. We also simplify the notations when compared with the Lagrangian formalism by exploiting the Hermitian symmetry satisfied by the velocity and buoyancy fields. These advantages allow us to recast the kinetic equation of IGWs into a canonical form, that is more amenable to analytical and numerical treatments.
The remainder of the paper is as follows. In the next § 2, we present the poloidal–toroidal decomposition, which is very convenient for studying IGWs and for writing the equations of motion in the canonical variables. Section 3 is devoted to the kinetic description of weak IGWs. The kinetic equation is derived in § 3.1 using standard assumptions of WWT. In § 3.2, we look for steady, scale-invariant solutions to the kinetic equation. We show in § 3.3 that, when evaluated on the resonant manifold, the interaction coefficients are symmetric with respect to permutation of the wave vectors. It allows us to write the canonical form of the kinetic equation. We also parametrize the resonant manifold, which allows us to give a simplified version of the collisional integral for axisymmetric spectra, and to study the transfer coefficients of triadic interactions. We study the hydrostatic limit in § 3.4. In that limit, our kinetic equation is equivalent to many previous ones in that case. We show that the PR spectrum (Pelinovsky & Raevsky Reference Pelinovsky and Raevsky1977) can be obtained without using the frequency resonance condition, which, up to our knowledge, was not remarked before. We conclude in § 4. Technical details about the derivation of the kinetic equation are presented in Appendix A.
2. Equations of motion
We start from the three-dimensional Boussinesq equations
where ![]() $(x,y,z)$ denote the three spatial coordinates in the Cartesian frame
$(x,y,z)$ denote the three spatial coordinates in the Cartesian frame ![]() $(O, \boldsymbol {e}_x, \boldsymbol {e}_y, \boldsymbol {e}_z)$,
$(O, \boldsymbol {e}_x, \boldsymbol {e}_y, \boldsymbol {e}_z)$, ![]() $\boldsymbol {e}_z$ is the unitary vector along the stratification axis,
$\boldsymbol {e}_z$ is the unitary vector along the stratification axis, ![]() $\boldsymbol {u}=(u_x, u_y, u_z)$ the velocity,
$\boldsymbol {u}=(u_x, u_y, u_z)$ the velocity, ![]() $b$ the buoyancy,
$b$ the buoyancy, ![]() $p$ the total kinematic pressure and
$p$ the total kinematic pressure and ![]() $N$ the Brunt–Väisälä (or buoyancy) frequency. The buoyancy is defined as
$N$ the Brunt–Väisälä (or buoyancy) frequency. The buoyancy is defined as ![]() $b = -g \rho ' / \rho _0$, where
$b = -g \rho ' / \rho _0$, where ![]() $g$ is the acceleration due to gravity,
$g$ is the acceleration due to gravity, ![]() $\rho _0$ is the average density of the fluid at
$\rho _0$ is the average density of the fluid at ![]() $z=0$ and
$z=0$ and ![]() $\rho '$ is the density perturbation with respect to the average linear density profile
$\rho '$ is the density perturbation with respect to the average linear density profile ![]() $\bar {\rho }(z) = \rho _0 + ({\mathrm {d} \bar {\rho }}/{\mathrm {d} z})z$. It follows that
$\bar {\rho }(z) = \rho _0 + ({\mathrm {d} \bar {\rho }}/{\mathrm {d} z})z$. It follows that ![]() $N = \sqrt {-({g}/{\rho _0})({\mathrm {d} \bar {\rho }}/{\mathrm {d} z})}$. Equations ((2.1)–(2.3)) conserve the total energy
$N = \sqrt {-({g}/{\rho _0})({\mathrm {d} \bar {\rho }}/{\mathrm {d} z})}$. Equations ((2.1)–(2.3)) conserve the total energy ![]() $E$ and the potential vorticity
$E$ and the potential vorticity ![]() $\varPi$ is a Lagrangian invariant (Bartello Reference Bartello1995), with
$\varPi$ is a Lagrangian invariant (Bartello Reference Bartello1995), with
with ![]() $\boldsymbol {\varOmega } = \boldsymbol {\nabla } \times \boldsymbol {u}$ being the vorticity.
$\boldsymbol {\varOmega } = \boldsymbol {\nabla } \times \boldsymbol {u}$ being the vorticity.
We consider a triply periodic domain with spatial periods ![]() $L_x = L_y = L_z = L$. The Fourier transform of the velocity field
$L_x = L_y = L_z = L$. The Fourier transform of the velocity field ![]() $\hat {\boldsymbol {u}}_{\boldsymbol {k}} = (\hat {u}_{x \boldsymbol {k}}, \hat {u}_{y \boldsymbol {k}}, \hat {u}_{z \boldsymbol {k}})$ can be written using the poloidal–toroidal-shear decomposition (Craya Reference Craya1957; Herring Reference Herring1974; Godeferd et al. Reference Godeferd, Delache and Cambon2010), which is now common in the study of stratified flows. Namely, we have
$\hat {\boldsymbol {u}}_{\boldsymbol {k}} = (\hat {u}_{x \boldsymbol {k}}, \hat {u}_{y \boldsymbol {k}}, \hat {u}_{z \boldsymbol {k}})$ can be written using the poloidal–toroidal-shear decomposition (Craya Reference Craya1957; Herring Reference Herring1974; Godeferd et al. Reference Godeferd, Delache and Cambon2010), which is now common in the study of stratified flows. Namely, we have
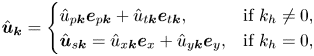 \begin{equation} \hat{\boldsymbol{u}}_{\boldsymbol{k}} = \begin{cases} \hat{u}_{p\boldsymbol{k}} \boldsymbol{e}_{p\boldsymbol{k}} + \hat{u}_{t\boldsymbol{k}} \boldsymbol{e}_{t\boldsymbol{k}}, & \text{if}\ k_h \neq 0, \\ \hat{\boldsymbol{u}}_{s\boldsymbol{k}} = \hat{u}_{x\boldsymbol{k}} \boldsymbol{e}_x + \hat{u}_{y\boldsymbol{k}} \boldsymbol{e}_y, & \text{if}\ k_h = 0, \end{cases} \end{equation}
\begin{equation} \hat{\boldsymbol{u}}_{\boldsymbol{k}} = \begin{cases} \hat{u}_{p\boldsymbol{k}} \boldsymbol{e}_{p\boldsymbol{k}} + \hat{u}_{t\boldsymbol{k}} \boldsymbol{e}_{t\boldsymbol{k}}, & \text{if}\ k_h \neq 0, \\ \hat{\boldsymbol{u}}_{s\boldsymbol{k}} = \hat{u}_{x\boldsymbol{k}} \boldsymbol{e}_x + \hat{u}_{y\boldsymbol{k}} \boldsymbol{e}_y, & \text{if}\ k_h = 0, \end{cases} \end{equation}where
where ![]() $\hat {u}_{p\boldsymbol {k}}$ is the poloidal component,
$\hat {u}_{p\boldsymbol {k}}$ is the poloidal component, ![]() $\hat {u}_{t\boldsymbol {k}}$ the toroidal component,
$\hat {u}_{t\boldsymbol {k}}$ the toroidal component, ![]() $\hat {\boldsymbol {u}}_{s\boldsymbol {k}}$ the shear modes component,
$\hat {\boldsymbol {u}}_{s\boldsymbol {k}}$ the shear modes component, ![]() $\boldsymbol {k}=(k_x, k_y, k_z)$ denotes the wave vector,
$\boldsymbol {k}=(k_x, k_y, k_z)$ denotes the wave vector, ![]() $k =|\boldsymbol {k}| = \sqrt {k_x^2 + k_y^2 + k_z^2}$ its modulus and
$k =|\boldsymbol {k}| = \sqrt {k_x^2 + k_y^2 + k_z^2}$ its modulus and ![]() $k_h = \sqrt {k_x^2 + k_y^2}$. The basis
$k_h = \sqrt {k_x^2 + k_y^2}$. The basis ![]() $(\boldsymbol {e}_{\boldsymbol {k}}, \boldsymbol {e}_{p\boldsymbol {k}}, \boldsymbol {e}_{t\boldsymbol {k}})$ is shown in figure 1.
$(\boldsymbol {e}_{\boldsymbol {k}}, \boldsymbol {e}_{p\boldsymbol {k}}, \boldsymbol {e}_{t\boldsymbol {k}})$ is shown in figure 1.
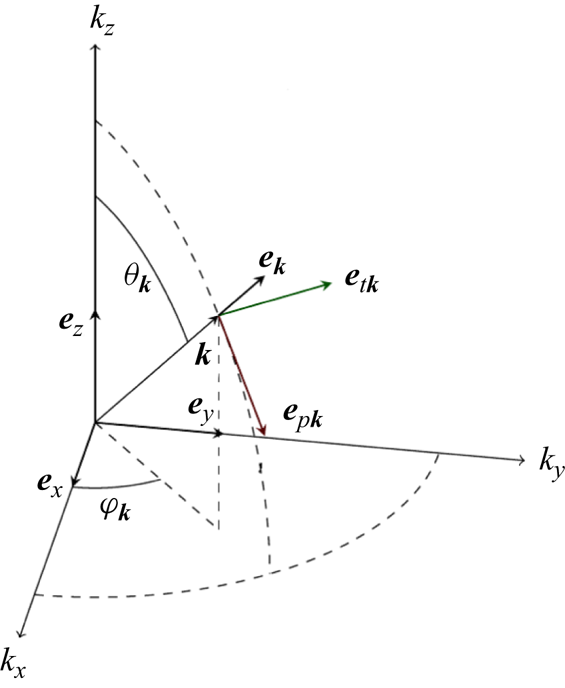
Figure 1. Illustration of the poloidal–toroidal basis ![]() $(\boldsymbol {e}_{\boldsymbol {k}}, \boldsymbol {e}_{p\boldsymbol {k}}, \boldsymbol {e}_{t\boldsymbol {k}})$ defined by (2.6a–c). Here,
$(\boldsymbol {e}_{\boldsymbol {k}}, \boldsymbol {e}_{p\boldsymbol {k}}, \boldsymbol {e}_{t\boldsymbol {k}})$ defined by (2.6a–c). Here, ![]() $\theta _{\boldsymbol {k}}$ is the polar angle (i.e. between
$\theta _{\boldsymbol {k}}$ is the polar angle (i.e. between ![]() $\boldsymbol {e}_z$ and
$\boldsymbol {e}_z$ and ![]() $\boldsymbol {e}_{\boldsymbol {k}}$), and
$\boldsymbol {e}_{\boldsymbol {k}}$), and ![]() $\varphi _{\boldsymbol {k}}$ is the azimuthal angle (i.e. between
$\varphi _{\boldsymbol {k}}$ is the azimuthal angle (i.e. between ![]() $\boldsymbol {e}_x$ and the horizontal projection of
$\boldsymbol {e}_x$ and the horizontal projection of ![]() $\boldsymbol {k}$).
$\boldsymbol {k}$).
In Fourier space, the equations of motion can be written as follows:
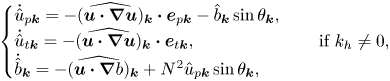 \begin{equation} \begin{cases}
\dot{\hat{u}}_{p\boldsymbol{k}} ={-}
(\widehat{\boldsymbol{u}\boldsymbol{\cdot}
\boldsymbol{\nabla} \boldsymbol{u}})_{\boldsymbol{k}}
\boldsymbol{\cdot} \boldsymbol{e}_{p\boldsymbol{k}} -
\hat{b}_{\boldsymbol{k}} \sin \theta_{\boldsymbol{k}},\\
\dot{\hat{u}}_{t\boldsymbol{k}} ={-}
(\widehat{\boldsymbol{u}\boldsymbol{\cdot}
\boldsymbol{\nabla} \boldsymbol{u}})_{\boldsymbol{k}}
\boldsymbol{\cdot} \boldsymbol{e}_{t\boldsymbol{k}},\\
\dot{\hat{b}}_{\boldsymbol{k}} ={-}
(\widehat{\boldsymbol{u}\boldsymbol{\cdot}
\boldsymbol{\nabla} b})_{\boldsymbol{k}} + N^2
\hat{u}_{p\boldsymbol{k}} \sin \theta_{\boldsymbol{k}},
\end{cases}\quad \text{if}\ k_h \neq 0 ,
\end{equation}
\begin{equation} \begin{cases}
\dot{\hat{u}}_{p\boldsymbol{k}} ={-}
(\widehat{\boldsymbol{u}\boldsymbol{\cdot}
\boldsymbol{\nabla} \boldsymbol{u}})_{\boldsymbol{k}}
\boldsymbol{\cdot} \boldsymbol{e}_{p\boldsymbol{k}} -
\hat{b}_{\boldsymbol{k}} \sin \theta_{\boldsymbol{k}},\\
\dot{\hat{u}}_{t\boldsymbol{k}} ={-}
(\widehat{\boldsymbol{u}\boldsymbol{\cdot}
\boldsymbol{\nabla} \boldsymbol{u}})_{\boldsymbol{k}}
\boldsymbol{\cdot} \boldsymbol{e}_{t\boldsymbol{k}},\\
\dot{\hat{b}}_{\boldsymbol{k}} ={-}
(\widehat{\boldsymbol{u}\boldsymbol{\cdot}
\boldsymbol{\nabla} b})_{\boldsymbol{k}} + N^2
\hat{u}_{p\boldsymbol{k}} \sin \theta_{\boldsymbol{k}},
\end{cases}\quad \text{if}\ k_h \neq 0 ,
\end{equation}and
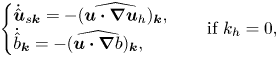 \begin{equation} \begin{cases} \dot{\hat{\boldsymbol{u}}}_{s\boldsymbol{k}} ={-} (\widehat{\boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{u}_h})_{\boldsymbol{k}} ,\\ \dot{\hat{b}}_{\boldsymbol{k}} ={-} (\widehat{\boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} b})_{\boldsymbol{k}}, \end{cases} \quad \text{if}\ k_h = 0 , \end{equation}
\begin{equation} \begin{cases} \dot{\hat{\boldsymbol{u}}}_{s\boldsymbol{k}} ={-} (\widehat{\boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{u}_h})_{\boldsymbol{k}} ,\\ \dot{\hat{b}}_{\boldsymbol{k}} ={-} (\widehat{\boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} b})_{\boldsymbol{k}}, \end{cases} \quad \text{if}\ k_h = 0 , \end{equation}
where ![]() $\boldsymbol {u}_h = (u_x,u_y,0)$ is the horizontal component of
$\boldsymbol {u}_h = (u_x,u_y,0)$ is the horizontal component of ![]() $\boldsymbol {u}$. In the linear regime, the poloidal velocity and the buoyancy are coupled, while the toroidal velocity and shear modes are decoupled and not evolving. The coupling between poloidal velocity and buoyancy is responsible for the propagation of IGWs with frequency
$\boldsymbol {u}$. In the linear regime, the poloidal velocity and the buoyancy are coupled, while the toroidal velocity and shear modes are decoupled and not evolving. The coupling between poloidal velocity and buoyancy is responsible for the propagation of IGWs with frequency
where ![]() $\theta _{\boldsymbol {k}}$ is the polar angle (figure 1). Equations (2.7) show that both shear modes and toroidal components have zero frequency in the linear regime, and hence they are not waves. More precisely, in the context of stratified turbulence,
$\theta _{\boldsymbol {k}}$ is the polar angle (figure 1). Equations (2.7) show that both shear modes and toroidal components have zero frequency in the linear regime, and hence they are not waves. More precisely, in the context of stratified turbulence, ![]() $\hat {u}_{p\boldsymbol {k}}$ is the kinetic part of linear waves (horizontal and vertical oscillations) while
$\hat {u}_{p\boldsymbol {k}}$ is the kinetic part of linear waves (horizontal and vertical oscillations) while ![]() $\hat {u}_{t\boldsymbol {k}}$ corresponds to vertical vortices. It makes the poloidal-toroidal-shear decomposition particularly suitable for studying IGWs and, more generally, flows with statistical axisymmetry (Godeferd et al. Reference Godeferd, Delache and Cambon2010; Yokoyama & Takaoka Reference Yokoyama and Takaoka2019; Maffioli, Delache & Godeferd Reference Maffioli, Delache and Godeferd2020). When compared with Caillol & Zeitlin (Reference Caillol and Zeitlin2000), the poloidal velocity encompasses both the potential part of the horizontal velocity and the vertical velocity, which simplifies the computations.
$\hat {u}_{t\boldsymbol {k}}$ corresponds to vertical vortices. It makes the poloidal-toroidal-shear decomposition particularly suitable for studying IGWs and, more generally, flows with statistical axisymmetry (Godeferd et al. Reference Godeferd, Delache and Cambon2010; Yokoyama & Takaoka Reference Yokoyama and Takaoka2019; Maffioli, Delache & Godeferd Reference Maffioli, Delache and Godeferd2020). When compared with Caillol & Zeitlin (Reference Caillol and Zeitlin2000), the poloidal velocity encompasses both the potential part of the horizontal velocity and the vertical velocity, which simplifies the computations.
In this study, we consider a flow composed of waves only, such that there are no toroidal and shear components. Neglecting the toroidal component is equivalent to neglecting vertical vorticity (Caillol & Zeitlin Reference Caillol and Zeitlin2000), or neglecting the ‘vortex’ part in the ‘wave-vortex’ decomposition in isopycnal coordinates (Lvov & Tabak Reference Lvov and Tabak2001). Ignoring the shear and toroidal components constitutes a standard assumption in IGW turbulence theory. Since the poloidal velocity and the buoyancy are real valued, their Fourier transforms satisfy the Hermitian symmetry. This symmetry allows us, as customary in WWT, to define the general complex wave mode ![]() $a_{\boldsymbol {k}} = ({1}/{\sqrt {2\omega _{\boldsymbol {k}}}}) (\hat {u}_{p\boldsymbol {k}} - {\rm i}({\hat {b}_{\boldsymbol {k}}}/{N}))$, which fully determines the wave dynamics (including positive and negative frequency branches). The poloidal and buoyancy modes then express as follows:
$a_{\boldsymbol {k}} = ({1}/{\sqrt {2\omega _{\boldsymbol {k}}}}) (\hat {u}_{p\boldsymbol {k}} - {\rm i}({\hat {b}_{\boldsymbol {k}}}/{N}))$, which fully determines the wave dynamics (including positive and negative frequency branches). The poloidal and buoyancy modes then express as follows:
The dynamical equation then reads
with the interaction coefficients
 \begin{align} V_{\boldsymbol{k}_1
\boldsymbol{k}_2}^{\boldsymbol{k}} &\equiv
V_{12}^{\boldsymbol{k}} = \sqrt{\frac{\omega_{1}
\omega_{2}}{32 \omega_{\boldsymbol{k}}}} \left[ \left(
\boldsymbol{e}_{p1} \boldsymbol{\cdot} \boldsymbol{k}
\right) \left( \boldsymbol{e}_{p2} \boldsymbol{\cdot}
\boldsymbol{e}_{p\boldsymbol{k}} \right)\right.\nonumber\\
&\quad + \left.
\boldsymbol{e}_{p1} \boldsymbol{\cdot} \boldsymbol{k}_2 +
\left( \boldsymbol{e}_{p2} \boldsymbol{\cdot}
\boldsymbol{k} \right) \left( \boldsymbol{e}_{p1}
\boldsymbol{\cdot} \boldsymbol{e}_{p\boldsymbol{k}} \right)
+ \boldsymbol{e}_{p2} \boldsymbol{\cdot} \boldsymbol{k}_1
\right] ,
\end{align}
\begin{align} V_{\boldsymbol{k}_1
\boldsymbol{k}_2}^{\boldsymbol{k}} &\equiv
V_{12}^{\boldsymbol{k}} = \sqrt{\frac{\omega_{1}
\omega_{2}}{32 \omega_{\boldsymbol{k}}}} \left[ \left(
\boldsymbol{e}_{p1} \boldsymbol{\cdot} \boldsymbol{k}
\right) \left( \boldsymbol{e}_{p2} \boldsymbol{\cdot}
\boldsymbol{e}_{p\boldsymbol{k}} \right)\right.\nonumber\\
&\quad + \left.
\boldsymbol{e}_{p1} \boldsymbol{\cdot} \boldsymbol{k}_2 +
\left( \boldsymbol{e}_{p2} \boldsymbol{\cdot}
\boldsymbol{k} \right) \left( \boldsymbol{e}_{p1}
\boldsymbol{\cdot} \boldsymbol{e}_{p\boldsymbol{k}} \right)
+ \boldsymbol{e}_{p2} \boldsymbol{\cdot} \boldsymbol{k}_1
\right] ,
\end{align}
and ![]() $\delta _{12}^{\boldsymbol {k}}$ (respectively
$\delta _{12}^{\boldsymbol {k}}$ (respectively ![]() $\delta _{12\boldsymbol {k}}$) being the Kronecker symbol enforcing the condition
$\delta _{12\boldsymbol {k}}$) being the Kronecker symbol enforcing the condition ![]() $\boldsymbol {k}_1 + \boldsymbol {k}_2 = \boldsymbol {k}$ (respectively
$\boldsymbol {k}_1 + \boldsymbol {k}_2 = \boldsymbol {k}$ (respectively ![]() $\boldsymbol {k}_1 + \boldsymbol {k}_2 + \boldsymbol {k} = 0$). Note that (2.10) is equivalent to the Boussinesq equations without toroidal velocity and shear modes. The sums represent nonlinear interaction between the wave modes. This equation has a convenient structure for deriving the wave-kinetic equation.
$\boldsymbol {k}_1 + \boldsymbol {k}_2 + \boldsymbol {k} = 0$). Note that (2.10) is equivalent to the Boussinesq equations without toroidal velocity and shear modes. The sums represent nonlinear interaction between the wave modes. This equation has a convenient structure for deriving the wave-kinetic equation.
By construction, the interaction coefficients ![]() $V_{12}^{\boldsymbol {k}}$ are symmetric with respect to the permutation of lower indices, i.e.
$V_{12}^{\boldsymbol {k}}$ are symmetric with respect to the permutation of lower indices, i.e. ![]() $V_{12}^{\boldsymbol {k}} = V_{21}^{\boldsymbol {k}}$, but a priori not symmetric with respect to the permutation between a lower index and the upper index. This complication prevents us from writing a canonical Hamiltonian equation for
$V_{12}^{\boldsymbol {k}} = V_{21}^{\boldsymbol {k}}$, but a priori not symmetric with respect to the permutation between a lower index and the upper index. This complication prevents us from writing a canonical Hamiltonian equation for ![]() $a_{\boldsymbol {k}}$. It is easy to show that the frequency is homogeneous,
$a_{\boldsymbol {k}}$. It is easy to show that the frequency is homogeneous, ![]() $\omega _{\mu \boldsymbol {k}} = \mu ^\alpha \omega _{\boldsymbol {k}}$, with homogeneity degree
$\omega _{\mu \boldsymbol {k}} = \mu ^\alpha \omega _{\boldsymbol {k}}$, with homogeneity degree ![]() $\alpha =0$. Also, the interaction coefficients are homogeneous, i.e.
$\alpha =0$. Also, the interaction coefficients are homogeneous, i.e. ![]() $V_{\mu \boldsymbol {k}_1 \mu \boldsymbol {k}_2}^{\mu \boldsymbol {k}} = \mu ^\beta V_{12}^{\boldsymbol {k}}$, with homogeneity degree
$V_{\mu \boldsymbol {k}_1 \mu \boldsymbol {k}_2}^{\mu \boldsymbol {k}} = \mu ^\beta V_{12}^{\boldsymbol {k}}$, with homogeneity degree ![]() $\beta =1$. Using the fact that
$\beta =1$. Using the fact that ![]() $\boldsymbol {e}_{p\boldsymbol {k}} \boldsymbol {\cdot } \boldsymbol {k} = 0$, it is easy to show that the interaction coefficients satisfy the following useful relations:
$\boldsymbol {e}_{p\boldsymbol {k}} \boldsymbol {\cdot } \boldsymbol {k} = 0$, it is easy to show that the interaction coefficients satisfy the following useful relations:
Note that such relations between interaction coefficients are common to fluid dynamical systems with quadratic invariants (see Appendix B of Remmel & Smith (Reference Remmel and Smith2009) for a general proof). It allows us to prove that the wave-action equation (2.10) conserves the energy (2.4)
 \begin{equation} E = \sum_{\boldsymbol{k}} \left[ \frac{|\hat{\boldsymbol{u}}_{\boldsymbol{k}}|^2}{2} + \frac{|\hat{b}_{\boldsymbol{k}}|^2}{2N^2} \right] = \sum_{\boldsymbol{k}} \omega_{\boldsymbol{k}} |a_{\boldsymbol{k}}|^2. \end{equation}
\begin{equation} E = \sum_{\boldsymbol{k}} \left[ \frac{|\hat{\boldsymbol{u}}_{\boldsymbol{k}}|^2}{2} + \frac{|\hat{b}_{\boldsymbol{k}}|^2}{2N^2} \right] = \sum_{\boldsymbol{k}} \omega_{\boldsymbol{k}} |a_{\boldsymbol{k}}|^2. \end{equation} On the manifold ![]() $\boldsymbol {k} = \boldsymbol {k}_1 + \boldsymbol {k}_2$ (or permutations), the interaction coefficients are only functions of
$\boldsymbol {k} = \boldsymbol {k}_1 + \boldsymbol {k}_2$ (or permutations), the interaction coefficients are only functions of ![]() $(k_h,k_{1h},k_{2h},k_{1z},k_{2z})$ or, alternatively, of
$(k_h,k_{1h},k_{2h},k_{1z},k_{2z})$ or, alternatively, of ![]() $(k_h,k_{1h},k_{2h},\theta _{1},\theta _{2})$. Because
$(k_h,k_{1h},k_{2h},\theta _{1},\theta _{2})$. Because ![]() $(\boldsymbol {k}_h,\boldsymbol {k}_{1h},\boldsymbol {k}_{2h})$ form a triangle, they must satisfy the triangular inequalities
$(\boldsymbol {k}_h,\boldsymbol {k}_{1h},\boldsymbol {k}_{2h})$ form a triangle, they must satisfy the triangular inequalities
meaning that ![]() $(k_{1h},k_{2h})$ must lie in the so-called ‘kinematic box’ (Lvov et al. Reference Lvov, Polzin and Yokoyama2012) shown in figure 2(a). We have checked numerically that the interaction coefficients are not fully symmetric with respect to permutations of indices, i.e.
$(k_{1h},k_{2h})$ must lie in the so-called ‘kinematic box’ (Lvov et al. Reference Lvov, Polzin and Yokoyama2012) shown in figure 2(a). We have checked numerically that the interaction coefficients are not fully symmetric with respect to permutations of indices, i.e. ![]() $V_{12}^{\boldsymbol {k}} \delta _{12}^{\boldsymbol {k}} \neq V_{\boldsymbol{k} 2}^{1} \delta _{12}^{\boldsymbol {k}} \neq V_{\boldsymbol{k} 1}^{2} \delta _{12}^{\boldsymbol {k}}$, as shown in figure 2(b).
$V_{12}^{\boldsymbol {k}} \delta _{12}^{\boldsymbol {k}} \neq V_{\boldsymbol{k} 2}^{1} \delta _{12}^{\boldsymbol {k}} \neq V_{\boldsymbol{k} 1}^{2} \delta _{12}^{\boldsymbol {k}}$, as shown in figure 2(b).
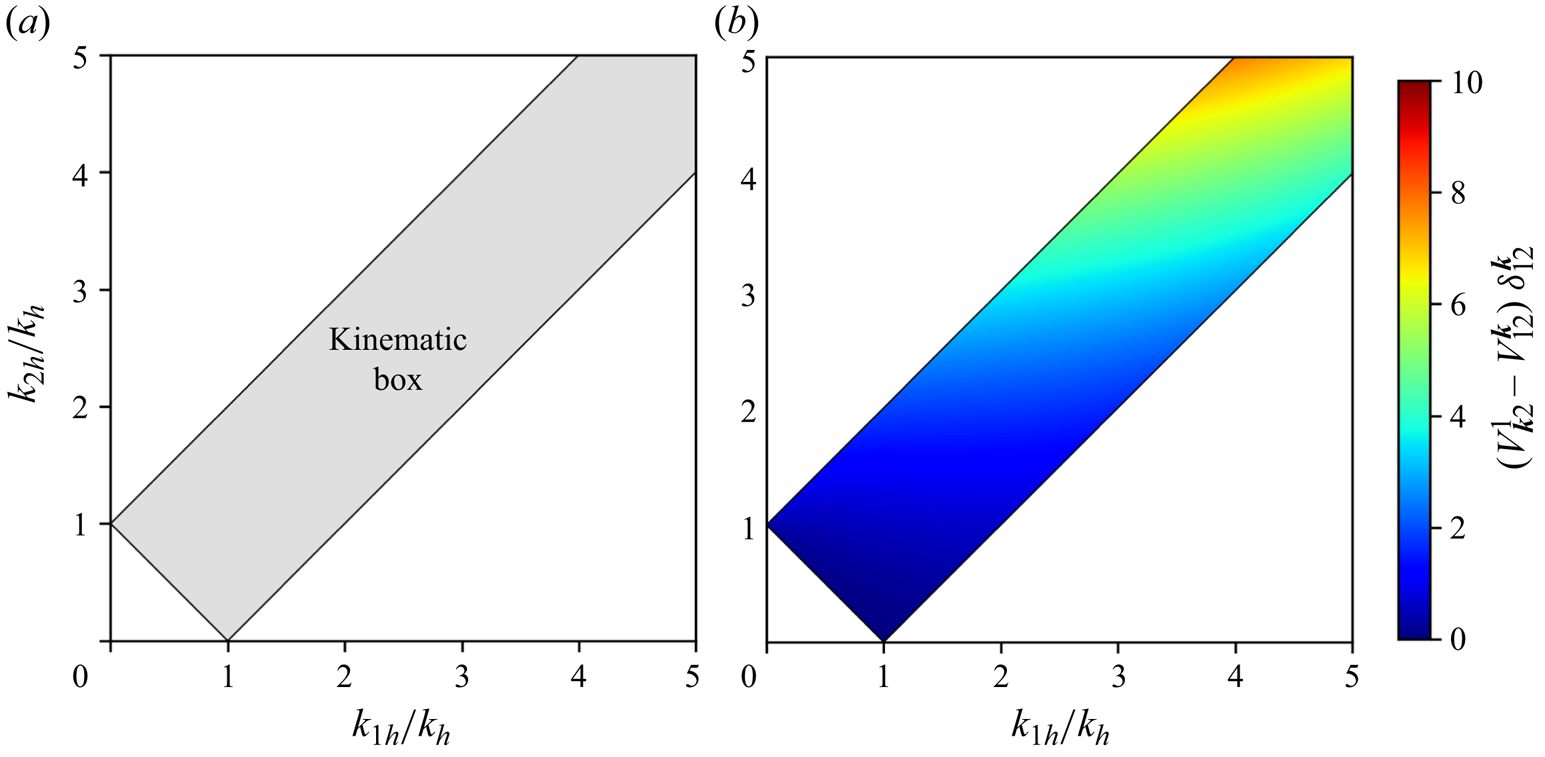
Figure 2. (a) Kinematic box defined by the conditions (2.14a–c). (b) Difference between the interaction coefficients ![]() $V_{12}^{\boldsymbol {k}}$ and
$V_{12}^{\boldsymbol {k}}$ and ![]() $V_{\boldsymbol{k} 2}^{1}$ when evaluated on the manifold
$V_{\boldsymbol{k} 2}^{1}$ when evaluated on the manifold ![]() $\boldsymbol {k} = \boldsymbol {k}_1 + \boldsymbol {k}_2$ for
$\boldsymbol {k} = \boldsymbol {k}_1 + \boldsymbol {k}_2$ for ![]() $(k_h=1, k_{1h}, k_{2h}, \theta _{1} = {\rm \pi}/4, \theta _{2}={\rm \pi} /6)$ and
$(k_h=1, k_{1h}, k_{2h}, \theta _{1} = {\rm \pi}/4, \theta _{2}={\rm \pi} /6)$ and ![]() $N=1$.
$N=1$.
3. Kinetic description
3.1. Wave-kinetic equation
The derivation of the kinetic equation is a long, but standard exercise in WWT (Hasselmann Reference Hasselmann1966; Zakharov et al. Reference Zakharov, L'vov and Falkovich1992; Nazarenko Reference Nazarenko2011; Galtier Reference Galtier2022). Since the present system does not have a canonical Hamiltonian structure, the final results cannot be anticipated. Assuming a time scale separation between the linear and the nonlinear times, we introduce the interaction representation variable as
where the parameter ![]() $\epsilon \ll 1$ quantifies the strength of the nonlinearity. For stratified flows,
$\epsilon \ll 1$ quantifies the strength of the nonlinearity. For stratified flows, ![]() $\epsilon$ corresponds to the Froude number
$\epsilon$ corresponds to the Froude number ![]() $Fr$. Using (2.10), we obtain
$Fr$. Using (2.10), we obtain
where ![]() $\omega _{12}^{\boldsymbol {k}} \equiv \omega _{\boldsymbol {k}} - \omega _{1} - \omega _{2}$ and
$\omega _{12}^{\boldsymbol {k}} \equiv \omega _{\boldsymbol {k}} - \omega _{1} - \omega _{2}$ and ![]() $\omega _{\boldsymbol {k} 1 2} \equiv - \omega _{\boldsymbol {k}} - \omega _{1} - \omega _{2}$. The derivation of the kinetic equation describing the evolution of the wave-action spectrum
$\omega _{\boldsymbol {k} 1 2} \equiv - \omega _{\boldsymbol {k}} - \omega _{1} - \omega _{2}$. The derivation of the kinetic equation describing the evolution of the wave-action spectrum
in the infinite size limit (![]() $L \rightarrow \infty$) and in the small nonlinearity limit (
$L \rightarrow \infty$) and in the small nonlinearity limit (![]() $\epsilon \rightarrow 0$) is given in Appendix A. These computations follow the steps described in Nazarenko (Reference Nazarenko2011). The final result is
$\epsilon \rightarrow 0$) is given in Appendix A. These computations follow the steps described in Nazarenko (Reference Nazarenko2011). The final result is
It can be shown that this kinetic equation is equivalent to the one derived by Caillol & Zeitlin (Reference Caillol and Zeitlin2000). Equations ((3.4)–(3.6)) are relatively compact and more suitable for theoretical treatments. The total wave energy balance equation is
 \begin{align} &= 4 {\rm \pi}\epsilon^2 \int \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2) \delta(\omega_{12}^{\boldsymbol{k}}) \nonumber\\&\quad \times \left( \omega_{\boldsymbol{k}} V_{12}^{\boldsymbol{k}} - \omega_{1} V_{\boldsymbol{k}2}^{1} - \omega_{2} V_{\boldsymbol{k}1}^{2} \right) \left( V_{12}^{\boldsymbol{k}} n_1 n_2 - V_{\boldsymbol{k}1}^{2} n_{\boldsymbol{k}} n_1 - V_{\boldsymbol{k}2}^{1} n_{\boldsymbol{k}} n_2 \right) \,\mathrm{d}^3\boldsymbol{k} \,\mathrm{d}^3\boldsymbol{k}_1 \,\mathrm{d}^3\boldsymbol{k}_2, \end{align}
\begin{align} &= 4 {\rm \pi}\epsilon^2 \int \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2) \delta(\omega_{12}^{\boldsymbol{k}}) \nonumber\\&\quad \times \left( \omega_{\boldsymbol{k}} V_{12}^{\boldsymbol{k}} - \omega_{1} V_{\boldsymbol{k}2}^{1} - \omega_{2} V_{\boldsymbol{k}1}^{2} \right) \left( V_{12}^{\boldsymbol{k}} n_1 n_2 - V_{\boldsymbol{k}1}^{2} n_{\boldsymbol{k}} n_1 - V_{\boldsymbol{k}2}^{1} n_{\boldsymbol{k}} n_2 \right) \,\mathrm{d}^3\boldsymbol{k} \,\mathrm{d}^3\boldsymbol{k}_1 \,\mathrm{d}^3\boldsymbol{k}_2, \end{align}
which is zero because of the symmetry of the interaction coefficients (2.12a,b). Note that it is not necessary to use the resonance condition in frequencies to prove that the kinetic equation conserves energy; ![]() $E$ is also an invariant of the Boussinesq equations ((2.1)–(2.3)) and of the wave-action equation (2.10).
$E$ is also an invariant of the Boussinesq equations ((2.1)–(2.3)) and of the wave-action equation (2.10).
For now, the kinetic equation ((3.4)–(3.6)) does not take a standard form typical for canonical Hamiltonian systems, except if the relation ![]() $\mathcal {R}_{12}^{\boldsymbol {k}} = \mathcal {Q}_{12}^{\boldsymbol {k}}$ holds. For this to happen,
$\mathcal {R}_{12}^{\boldsymbol {k}} = \mathcal {Q}_{12}^{\boldsymbol {k}}$ holds. For this to happen, ![]() $V_{12}^{\boldsymbol {k}}$ should be fully symmetric with respect to the
$V_{12}^{\boldsymbol {k}}$ should be fully symmetric with respect to the ![]() $3$ indices when evaluated on the resonant manifold
$3$ indices when evaluated on the resonant manifold ![]() $\boldsymbol {k} = \boldsymbol {k}_1 + \boldsymbol {k}_2$,
$\boldsymbol {k} = \boldsymbol {k}_1 + \boldsymbol {k}_2$, ![]() $\omega _{\boldsymbol {k}} = \omega _{1} + \omega _{2}$ (or permutations) such that we could write
$\omega _{\boldsymbol {k}} = \omega _{1} + \omega _{2}$ (or permutations) such that we could write ![]() $V_{12}^{\boldsymbol {k}} = V_{\boldsymbol{k} 2}^{1} = V_{\boldsymbol{k} 1}^{2}$ in
$V_{12}^{\boldsymbol {k}} = V_{\boldsymbol{k} 2}^{1} = V_{\boldsymbol{k} 1}^{2}$ in ![]() $\mathcal {R}_{12}^{\boldsymbol {k}}$,
$\mathcal {R}_{12}^{\boldsymbol {k}}$, ![]() $\mathcal {Q}_{\boldsymbol{k} 2}^{1}$ and
$\mathcal {Q}_{\boldsymbol{k} 2}^{1}$ and ![]() $\mathcal {Q}_{\boldsymbol{k} 1}^{2}$. Such a symmetry could be expected since the kinetic equation obtained in the Lagrangian formalism is almost canonical (Hasselmann Reference Hasselmann1967; Müller & Olbers Reference Müller and Olbers1975; Olbers Reference Olbers1976). As already shown in figure 2(b), a resonance condition in wave vectors is not sufficient to have
$\mathcal {Q}_{\boldsymbol{k} 1}^{2}$. Such a symmetry could be expected since the kinetic equation obtained in the Lagrangian formalism is almost canonical (Hasselmann Reference Hasselmann1967; Müller & Olbers Reference Müller and Olbers1975; Olbers Reference Olbers1976). As already shown in figure 2(b), a resonance condition in wave vectors is not sufficient to have ![]() $V_{12}^{\boldsymbol {k}} = V_{\boldsymbol{k} 2}^{1} = V_{\boldsymbol{k} 1}^{2}$. However, adding the constraint of resonance condition in frequencies eventually allows to satisfy this symmetry, as will be explained in the § 3.3.
$V_{12}^{\boldsymbol {k}} = V_{\boldsymbol{k} 2}^{1} = V_{\boldsymbol{k} 1}^{2}$. However, adding the constraint of resonance condition in frequencies eventually allows to satisfy this symmetry, as will be explained in the § 3.3.
3.2. Steady, scale-invariant spectra
Despite its compact form, analytical solution to the kinetic equation (3.4) are not easy to find. The only exception is for ![]() $n_{\boldsymbol {k}} \propto 1/\omega _{\boldsymbol {k}}$, corresponding to the equilibrium (RJ) spectrum with equipartition of energy. It is worth mentioning that this RJ spectrum can be obtained without using the resonance condition in frequencies, but only the symmetry of the interaction coefficients (2.12a,b) when the wave vector resonance condition is satisfied. We can try to find other steady-state solutions to the kinetic equation, in the non-hydrostatic case, by using the ansatz
$n_{\boldsymbol {k}} \propto 1/\omega _{\boldsymbol {k}}$, corresponding to the equilibrium (RJ) spectrum with equipartition of energy. It is worth mentioning that this RJ spectrum can be obtained without using the resonance condition in frequencies, but only the symmetry of the interaction coefficients (2.12a,b) when the wave vector resonance condition is satisfied. We can try to find other steady-state solutions to the kinetic equation, in the non-hydrostatic case, by using the ansatz
corresponding to a separable, scale-invariant spectrum. We adapt the computations of Shavit, Bühler & Shatah (Reference Shavit, Bühler and Shatah2024) in order to find a possible value for the exponent ![]() $\nu$. We first write the evolution equation for the energy density averaged over angles
$\nu$. We first write the evolution equation for the energy density averaged over angles ![]() $e(k,t)$. Namely,
$e(k,t)$. Namely,
 \begin{align} \dot{e}(k,t) &= \int
\omega_{\boldsymbol{k}} \dot{n}_{\boldsymbol{k}} \sin
\theta_{\boldsymbol{k}} \,\mathrm{d}
\theta_{\boldsymbol{k}} \,\mathrm{d}
\varphi_{\boldsymbol{k}}\nonumber\\
&= \int \left[
\omega_{\boldsymbol{k}} \mathcal{R}_{12}^{\boldsymbol{k}} -
\omega_{\boldsymbol{k}} \mathcal{Q}_{\boldsymbol{k}2}^{1} -
\omega_{\boldsymbol{k}} \mathcal{Q}_{\boldsymbol{k}1}^{2}
\right] \,\mathrm{d}^3\boldsymbol{k}_1
\,\mathrm{d}^3\boldsymbol{k}_2 \sin \theta_{\boldsymbol{k}}
\,\mathrm{d} \theta_{\boldsymbol{k}} \,\mathrm{d}
\varphi_{\boldsymbol{k}}.
\end{align}
\begin{align} \dot{e}(k,t) &= \int
\omega_{\boldsymbol{k}} \dot{n}_{\boldsymbol{k}} \sin
\theta_{\boldsymbol{k}} \,\mathrm{d}
\theta_{\boldsymbol{k}} \,\mathrm{d}
\varphi_{\boldsymbol{k}}\nonumber\\
&= \int \left[
\omega_{\boldsymbol{k}} \mathcal{R}_{12}^{\boldsymbol{k}} -
\omega_{\boldsymbol{k}} \mathcal{Q}_{\boldsymbol{k}2}^{1} -
\omega_{\boldsymbol{k}} \mathcal{Q}_{\boldsymbol{k}1}^{2}
\right] \,\mathrm{d}^3\boldsymbol{k}_1
\,\mathrm{d}^3\boldsymbol{k}_2 \sin \theta_{\boldsymbol{k}}
\,\mathrm{d} \theta_{\boldsymbol{k}} \,\mathrm{d}
\varphi_{\boldsymbol{k}}.
\end{align}
In steady state, the integral on the right-hand side of (3.11) must be zero. If we assume (3.10), this integral is also only a function of ![]() $k$ and
$k$ and ![]() $\nu$ and depends on the angular variable via some function
$\nu$ and depends on the angular variable via some function ![]() $f$. To find possible values for
$f$. To find possible values for ![]() $\nu$, we adapt the Zakharov transformation, so we replace
$\nu$, we adapt the Zakharov transformation, so we replace
in the integral with ![]() $\mathcal {Q}_{\boldsymbol{k} 2}^{1}$, and a similar transformation for the integral with
$\mathcal {Q}_{\boldsymbol{k} 2}^{1}$, and a similar transformation for the integral with ![]() $\mathcal {Q}_{\boldsymbol{k} 1}^{2}$ in (3.11). We then obtain the stationarity condition
$\mathcal {Q}_{\boldsymbol{k} 1}^{2}$ in (3.11). We then obtain the stationarity condition
 \begin{align} 0 &= 4 {\rm \pi}\epsilon^2 \int \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2) \delta(\omega_{12}^{\boldsymbol{k}}) \nonumber\\ & \quad \times \left[ \omega_{\boldsymbol{k}} V_{12}^{\boldsymbol{k}} - \left( \frac{k_1}{k} \right)^{\chi} \omega_{1} V_{\boldsymbol{k}2}^{1} - \left( \frac{k_2}{k} \right)^{\chi} \omega_{2} V_{\boldsymbol{k}1}^{2} \right]\nonumber\\ & \quad \times \left( V_{12}^{\boldsymbol{k}} n_1 n_2 - V_{\boldsymbol{k}1}^{2} n_{\boldsymbol{k}} n_1 - V_{\boldsymbol{k}2}^{1} n_{\boldsymbol{k}} n_2 \right) \,\mathrm{d}^3\boldsymbol{k}_1 \,\mathrm{d}^3\boldsymbol{k}_2 \sin \theta_{\boldsymbol{k}} \,\mathrm{d} \theta_{\boldsymbol{k}} \,\mathrm{d} \varphi_{\boldsymbol{k}} , \end{align}
\begin{align} 0 &= 4 {\rm \pi}\epsilon^2 \int \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2) \delta(\omega_{12}^{\boldsymbol{k}}) \nonumber\\ & \quad \times \left[ \omega_{\boldsymbol{k}} V_{12}^{\boldsymbol{k}} - \left( \frac{k_1}{k} \right)^{\chi} \omega_{1} V_{\boldsymbol{k}2}^{1} - \left( \frac{k_2}{k} \right)^{\chi} \omega_{2} V_{\boldsymbol{k}1}^{2} \right]\nonumber\\ & \quad \times \left( V_{12}^{\boldsymbol{k}} n_1 n_2 - V_{\boldsymbol{k}1}^{2} n_{\boldsymbol{k}} n_1 - V_{\boldsymbol{k}2}^{1} n_{\boldsymbol{k}} n_2 \right) \,\mathrm{d}^3\boldsymbol{k}_1 \,\mathrm{d}^3\boldsymbol{k}_2 \sin \theta_{\boldsymbol{k}} \,\mathrm{d} \theta_{\boldsymbol{k}} \,\mathrm{d} \varphi_{\boldsymbol{k}} , \end{align}
where ![]() $\chi \equiv \alpha - 2 \beta - 2 \nu - 2 d$, with
$\chi \equiv \alpha - 2 \beta - 2 \nu - 2 d$, with ![]() $d=3$ being the number of spatial dimensions. Condition (3.13) is satisfied when
$d=3$ being the number of spatial dimensions. Condition (3.13) is satisfied when ![]() $\chi = 0$ due to symmetry of the interaction coefficients (2.12a,b). It leads to the exponent
$\chi = 0$ due to symmetry of the interaction coefficients (2.12a,b). It leads to the exponent ![]() $\nu = -4$, which is consistent with the high-frequency limit of the Garrett–Munk spectrum (
$\nu = -4$, which is consistent with the high-frequency limit of the Garrett–Munk spectrum (![]() $\propto k_h^{-4} |k_z|^{0}$), the PR spectrum (
$\propto k_h^{-4} |k_z|^{0}$), the PR spectrum (![]() $\propto k_h^{-7/2} |k_z|^{-1/2}$), the spectrum obtained in the hydrostatic limit by considering ID triads only (Lanchon & Cortet Reference Lanchon and Cortet2023) (
$\propto k_h^{-7/2} |k_z|^{-1/2}$), the spectrum obtained in the hydrostatic limit by considering ID triads only (Lanchon & Cortet Reference Lanchon and Cortet2023) (![]() $\propto k_h^{-3} |k_z|^{-1}$) and oceanic measurements (Lvov et al. Reference Lvov, Polzin and Tabak2004).
$\propto k_h^{-3} |k_z|^{-1}$) and oceanic measurements (Lvov et al. Reference Lvov, Polzin and Tabak2004).
Testing the validity of ![]() $\nu = -4$ is beyond the scope of this study. For this, we need to show that the collision integral converges in the vicinity of
$\nu = -4$ is beyond the scope of this study. For this, we need to show that the collision integral converges in the vicinity of ![]() $\nu = -4$, for some yet unknown
$\nu = -4$, for some yet unknown ![]() $f(\theta _{\boldsymbol {k}},\varphi _{\boldsymbol {k}})$. This analysis has been done in the hydrostatic limit for bi-homogenous spectra
$f(\theta _{\boldsymbol {k}},\varphi _{\boldsymbol {k}})$. This analysis has been done in the hydrostatic limit for bi-homogenous spectra ![]() $\propto k_h^{\nu _h} |k_z|^{\nu _z}$, and it has been found that the line
$\propto k_h^{\nu _h} |k_z|^{\nu _z}$, and it has been found that the line ![]() $\nu = \nu _h + \nu _z = -4$ corresponds to non-physical spectra because of collision integral divergences (Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021). Yet, the divergence in the hydrostatic limit does not imply that
$\nu = \nu _h + \nu _z = -4$ corresponds to non-physical spectra because of collision integral divergences (Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021). Yet, the divergence in the hydrostatic limit does not imply that ![]() $\nu =-4$ is unrealizable outside this limit because the convergence conditions could be less restrictive in the non-hydrostatic case. Moreover, the ansatz (3.10) is more general than
$\nu =-4$ is unrealizable outside this limit because the convergence conditions could be less restrictive in the non-hydrostatic case. Moreover, the ansatz (3.10) is more general than ![]() $n_{\boldsymbol {k}} = C k_h^{\nu _h} |k_z|^{\nu _z}$, which may allow other local spectra. Finally, it is important to note that the angular dependence
$n_{\boldsymbol {k}} = C k_h^{\nu _h} |k_z|^{\nu _z}$, which may allow other local spectra. Finally, it is important to note that the angular dependence ![]() $f(\theta _{\boldsymbol {k}},\varphi _{\boldsymbol {k}})$ is embedded everywhere in the integrand in a non-trivial way and could lead to a cancellation of the collisional integral for
$f(\theta _{\boldsymbol {k}},\varphi _{\boldsymbol {k}})$ is embedded everywhere in the integrand in a non-trivial way and could lead to a cancellation of the collisional integral for ![]() $\nu \neq -4$. Indeed, the solution obtained by Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010) and Dematteis & Lvov (Reference Dematteis and Lvov2021) in the hydrostatic limit is of such a type.
$\nu \neq -4$. Indeed, the solution obtained by Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010) and Dematteis & Lvov (Reference Dematteis and Lvov2021) in the hydrostatic limit is of such a type.
3.3. Canonical form and resonant manifold
We proceed now to show that ![]() $V_{12}^{\boldsymbol {k}} = V_{\boldsymbol{k} 2}^{1} = V_{\boldsymbol{k} 1}^{2}$ on the resonant manifold, and thus that the kinetic equation (3.4) can be written in a canonical form. We first use the symmetry (2.12a,b), together with the resonance condition in frequencies
$V_{12}^{\boldsymbol {k}} = V_{\boldsymbol{k} 2}^{1} = V_{\boldsymbol{k} 1}^{2}$ on the resonant manifold, and thus that the kinetic equation (3.4) can be written in a canonical form. We first use the symmetry (2.12a,b), together with the resonance condition in frequencies ![]() $\omega _{\boldsymbol {k}} = \omega _{1} + \omega _{2}$, to readily show that
$\omega _{\boldsymbol {k}} = \omega _{1} + \omega _{2}$, to readily show that
Equation (3.14) has a simple geometrical meaning: the vectors ![]() $(V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 2}^{1}, V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 1}^{2})$ and
$(V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 2}^{1}, V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 1}^{2})$ and ![]() $(\omega _{1}, \omega _{2}=\omega _{\boldsymbol {k}}-\omega _{1})$ are orthogonal for all points of the resonant manifold. Because the
$(\omega _{1}, \omega _{2}=\omega _{\boldsymbol {k}}-\omega _{1})$ are orthogonal for all points of the resonant manifold. Because the ![]() $\omega _{\boldsymbol {k}}$ values only depend on the angles
$\omega _{\boldsymbol {k}}$ values only depend on the angles ![]() $\theta _{\boldsymbol {k}}$, to satisfy (3.14) while varying
$\theta _{\boldsymbol {k}}$, to satisfy (3.14) while varying ![]() $k$ and
$k$ and ![]() $k_1$ (at fixed angles), the vectors
$k_1$ (at fixed angles), the vectors ![]() $(V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 2}^{1}, V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 1}^{2})$ must remain co-linear. The orthogonality condition (3.14) thus leads to
$(V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 2}^{1}, V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 1}^{2})$ must remain co-linear. The orthogonality condition (3.14) thus leads to
 \begin{align} \left. \begin{pmatrix}
V_{12}^{\boldsymbol{k}} - V_{\boldsymbol{k}2}^{1} \\
V_{12}^{\boldsymbol{k}} - V_{\boldsymbol{k}1}^{2}
\end{pmatrix}
\right|_{(k,k_1,\theta_{\boldsymbol{k}},\theta_{1})} =
g(k,k_1) \left. \begin{pmatrix} V_{12}^{\boldsymbol{k}} -
V_{\boldsymbol{k}2}^{1} \\ V_{12}^{\boldsymbol{k}} -
V_{\boldsymbol{k}1}^{2}
\end{pmatrix}\right|_{(1,1,\theta_{\boldsymbol{k}},\theta_{1})}
\perp \begin{pmatrix} \omega_{1} \\ \omega_{2}
\end{pmatrix} \quad \forall (\omega_{1}, \omega_{2}),
\end{align}
\begin{align} \left. \begin{pmatrix}
V_{12}^{\boldsymbol{k}} - V_{\boldsymbol{k}2}^{1} \\
V_{12}^{\boldsymbol{k}} - V_{\boldsymbol{k}1}^{2}
\end{pmatrix}
\right|_{(k,k_1,\theta_{\boldsymbol{k}},\theta_{1})} =
g(k,k_1) \left. \begin{pmatrix} V_{12}^{\boldsymbol{k}} -
V_{\boldsymbol{k}2}^{1} \\ V_{12}^{\boldsymbol{k}} -
V_{\boldsymbol{k}1}^{2}
\end{pmatrix}\right|_{(1,1,\theta_{\boldsymbol{k}},\theta_{1})}
\perp \begin{pmatrix} \omega_{1} \\ \omega_{2}
\end{pmatrix} \quad \forall (\omega_{1}, \omega_{2}),
\end{align}
where ![]() $g$ is an unknown function that depends on
$g$ is an unknown function that depends on ![]() $k$ and
$k$ and ![]() $k_1$ only. We have used here the fact that the resonant manifold can be parametrized using the variables
$k_1$ only. We have used here the fact that the resonant manifold can be parametrized using the variables ![]() $(k,k_1,\theta _{\boldsymbol {k}},\theta _{1})$. Using (3.15) in (3.14), we see that whether
$(k,k_1,\theta _{\boldsymbol {k}},\theta _{1})$. Using (3.15) in (3.14), we see that whether ![]() $g(k,k_1)=0$, or
$g(k,k_1)=0$, or ![]() $\omega _{1} (V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 2}^{1})|_{(1,1,\theta _{\boldsymbol {k}},\theta _{1})} + \omega _{2} (V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 1}^{2})|_{(1,1,\theta _{\boldsymbol {k}},\theta _{1})}= 0$. Equation (3.15) therefore allows us to reduce the analysis to
$\omega _{1} (V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 2}^{1})|_{(1,1,\theta _{\boldsymbol {k}},\theta _{1})} + \omega _{2} (V_{12}^{\boldsymbol {k}} - V_{\boldsymbol{k} 1}^{2})|_{(1,1,\theta _{\boldsymbol {k}},\theta _{1})}= 0$. Equation (3.15) therefore allows us to reduce the analysis to ![]() $(k,k_1)=(1,1)$. Using the symbolic computational capabilities of the Mathematica software (Wolfram Research, Inc. 2024), we show in the supplementary material that
$(k,k_1)=(1,1)$. Using the symbolic computational capabilities of the Mathematica software (Wolfram Research, Inc. 2024), we show in the supplementary material that
 \begin{align} &\left.\left(
V_{12}^{\boldsymbol{k}} - V_{\boldsymbol{k}2}^{1}
\right)\right|_{(1,1,\theta_{\boldsymbol{k}},\theta_{1})}
={-}\sqrt{\frac{N}{128}}
\frac{1}{\cos(2\theta_{\boldsymbol{k}}) + \cos(2\theta_{1})
+ 4\sin\theta_{\boldsymbol{k}} \sin\theta_{1}}\nonumber\\
&\quad \times \left\{ \left[
\csc\left(\frac{\theta_{\boldsymbol{k}}-\theta_{1}}{2}\right)
\sin\left( \frac{\theta_{\boldsymbol{k}} +
\theta_{1}}{2}\right) \right. \right.\nonumber\\ &\quad
\times (9 \cos(2\theta_{\boldsymbol{k}}) -
3\cos(\theta_{\boldsymbol{k}}-3\theta_{1}) -
8\cos(2\theta_{\boldsymbol{k}}-2\theta_{1}) \nonumber\\
&\quad + 16\cos(\theta_{\boldsymbol{k}}-\theta_{1})
\nonumber\\ &\quad- 3 (4 +
\cos\left(3\theta_{\boldsymbol{k}}-\theta_{1}\right) -
3\cos(2\theta_{1}) +
4\cos(\theta_{\boldsymbol{k}}+\theta_{1}))) \nonumber\\
&\quad \times\left. \left. \left( \sqrt{-\csc\theta_{\boldsymbol{k}} +
\csc\theta_{1}} - \csc\theta_{1} \sqrt{\sin\theta_{1} -
\csc\theta_{\boldsymbol{k}} \sin^2\theta_{1}} \right)
\right] \right\} = 0.
\end{align}
\begin{align} &\left.\left(
V_{12}^{\boldsymbol{k}} - V_{\boldsymbol{k}2}^{1}
\right)\right|_{(1,1,\theta_{\boldsymbol{k}},\theta_{1})}
={-}\sqrt{\frac{N}{128}}
\frac{1}{\cos(2\theta_{\boldsymbol{k}}) + \cos(2\theta_{1})
+ 4\sin\theta_{\boldsymbol{k}} \sin\theta_{1}}\nonumber\\
&\quad \times \left\{ \left[
\csc\left(\frac{\theta_{\boldsymbol{k}}-\theta_{1}}{2}\right)
\sin\left( \frac{\theta_{\boldsymbol{k}} +
\theta_{1}}{2}\right) \right. \right.\nonumber\\ &\quad
\times (9 \cos(2\theta_{\boldsymbol{k}}) -
3\cos(\theta_{\boldsymbol{k}}-3\theta_{1}) -
8\cos(2\theta_{\boldsymbol{k}}-2\theta_{1}) \nonumber\\
&\quad + 16\cos(\theta_{\boldsymbol{k}}-\theta_{1})
\nonumber\\ &\quad- 3 (4 +
\cos\left(3\theta_{\boldsymbol{k}}-\theta_{1}\right) -
3\cos(2\theta_{1}) +
4\cos(\theta_{\boldsymbol{k}}+\theta_{1}))) \nonumber\\
&\quad \times\left. \left. \left( \sqrt{-\csc\theta_{\boldsymbol{k}} +
\csc\theta_{1}} - \csc\theta_{1} \sqrt{\sin\theta_{1} -
\csc\theta_{\boldsymbol{k}} \sin^2\theta_{1}} \right)
\right] \right\} = 0.
\end{align}It then follows from ((3.14)–(3.15)) that
which is the desired symmetry to put the kinetic equation in a canonical form.
The kinetic equation (3.4) can therefore be rewritten
Similarly to Rossby waves (Nazarenko Reference Nazarenko2011), the wave-action dynamics (2.10) does not have a canonical Hamiltonian structure, but the kinetic equation (3.18) is the same as if the system were canonical because of the resonance condition in frequencies. Namely, we could have obtained ((3.18)–(3.19)) by using the Hamilton equation ![]() ${\rm i}\dot {a}_{\boldsymbol {k}} = {\delta H_{eff}}/{\delta a_{\boldsymbol {k}}^*}$ together with the effective Hamiltonian
${\rm i}\dot {a}_{\boldsymbol {k}} = {\delta H_{eff}}/{\delta a_{\boldsymbol {k}}^*}$ together with the effective Hamiltonian ![]() $H_{eff} = \tfrac {1}{2} \sum _3 \omega _3 |a_3|^3 + \sum _{1,2,3} ( \delta _{12}^3 V_{12}^3 a_1 a_2 a_3^* + \delta _{23}^1 V_{23}^1 a_1^* a_2 a_3^* )$. Yet, it is not equivalent to the original wave mode equation (2.10) outside the resonant manifold.
$H_{eff} = \tfrac {1}{2} \sum _3 \omega _3 |a_3|^3 + \sum _{1,2,3} ( \delta _{12}^3 V_{12}^3 a_1 a_2 a_3^* + \delta _{23}^1 V_{23}^1 a_1^* a_2 a_3^* )$. Yet, it is not equivalent to the original wave mode equation (2.10) outside the resonant manifold.
In the case of a wave-action spectrum invariant under rotation around the stratification axis, i.e. ![]() $n_{\boldsymbol {k}}=n(k_h,k_z,t)$, the kinetic equation ((3.18)–(3.19)) takes a simpler form after integrating over azimuthal angles
$n_{\boldsymbol {k}}=n(k_h,k_z,t)$, the kinetic equation ((3.18)–(3.19)) takes a simpler form after integrating over azimuthal angles ![]() $(\varphi _{1},\varphi _{2})$
$(\varphi _{1},\varphi _{2})$
In the latter equations, the interaction coefficients are evaluated using ![]() $\boldsymbol {k}_h = \boldsymbol {k}_{1h} + \boldsymbol {k}_{2h}$, and similar relations obtained by permutations of wave vectors. It follows that they are functions of
$\boldsymbol {k}_h = \boldsymbol {k}_{1h} + \boldsymbol {k}_{2h}$, and similar relations obtained by permutations of wave vectors. It follows that they are functions of ![]() $(k_h, k_z, k_{1h}, k_{1z}, k_{2h}, k_{2z})$ only. The factor 2 arising in
$(k_h, k_z, k_{1h}, k_{1z}, k_{2h}, k_{2z})$ only. The factor 2 arising in ![]() $\mathcal {R}_{12}^{\boldsymbol {k}(h)}$ (3.21) when compared with
$\mathcal {R}_{12}^{\boldsymbol {k}(h)}$ (3.21) when compared with ![]() $\mathcal {R}_{12}^{\boldsymbol {k}}$ (3.19) comes from the fact that there are two solutions
$\mathcal {R}_{12}^{\boldsymbol {k}}$ (3.19) comes from the fact that there are two solutions ![]() $(\varphi _{1},\varphi _{2})$ to
$(\varphi _{1},\varphi _{2})$ to ![]() $\boldsymbol {k}_h = \boldsymbol {k}_{1h} + \boldsymbol {k}_{2h}$ (or permutations of wave vectors) for each
$\boldsymbol {k}_h = \boldsymbol {k}_{1h} + \boldsymbol {k}_{2h}$ (or permutations of wave vectors) for each ![]() $(k_h,k_z,k_{1h},k_{1z},k_{2h},k_{2z})$. Here,
$(k_h,k_z,k_{1h},k_{1z},k_{2h},k_{2z})$. Here, ![]() $\varDelta$ is the area of the triangle formed by the horizontal wave vectors. It arises from the average of
$\varDelta$ is the area of the triangle formed by the horizontal wave vectors. It arises from the average of ![]() $\delta (\boldsymbol {k}_h - \boldsymbol {k}_{1h} - \boldsymbol {k}_{2h})$. We can further simplify the collision integral (3.20) by working with polar coordinates
$\delta (\boldsymbol {k}_h - \boldsymbol {k}_{1h} - \boldsymbol {k}_{2h})$. We can further simplify the collision integral (3.20) by working with polar coordinates ![]() $(k_h,k_z)=k(\sin \theta _{\boldsymbol {k}}, \cos \theta _{\boldsymbol {k}})$,
$(k_h,k_z)=k(\sin \theta _{\boldsymbol {k}}, \cos \theta _{\boldsymbol {k}})$, ![]() $(k_{1h},k_{1z})=k_1(\sin \theta _{1}, \cos \theta _{1})$ and
$(k_{1h},k_{1z})=k_1(\sin \theta _{1}, \cos \theta _{1})$ and ![]() $(k_{2h},k_{2z})=k_2(\sin \theta _{2}, \cos \theta _{2})$. Because the last two terms of the collision integral are symmetric with respect to
$(k_{2h},k_{2z})=k_2(\sin \theta _{2}, \cos \theta _{2})$. Because the last two terms of the collision integral are symmetric with respect to ![]() $\boldsymbol {k}_1 \leftrightarrow \boldsymbol {k}_2$, we obtain
$\boldsymbol {k}_1 \leftrightarrow \boldsymbol {k}_2$, we obtain
 \begin{align}\mathcal{I}_{\boldsymbol{k}} &= 8 {\rm \pi}\epsilon^2 \int
\delta(k \cos \theta_{\boldsymbol{k}} - k_1 \cos \theta_{1}
- k_2 \cos \theta_{2}) \delta(N(\sin
\theta_{\boldsymbol{k}} - \sin \theta_{1} - \sin
\theta_{2}))\nonumber\\ &\quad \times
\frac{|V_{12}^{\boldsymbol{k}}|^2}{\varDelta} \left( n_1
n_2 - n_{\boldsymbol{k}} n_1 - n_{\boldsymbol{k}} n_2
\right) k_1^2 \sin \theta_{1} k_2^2 \sin \theta_{2}
\,\mathrm{d} \theta_{1} \,\mathrm{d} k_1 \,\mathrm{d}
\theta_{2} \,\mathrm{d} k_2,
\end{align}
\begin{align}\mathcal{I}_{\boldsymbol{k}} &= 8 {\rm \pi}\epsilon^2 \int
\delta(k \cos \theta_{\boldsymbol{k}} - k_1 \cos \theta_{1}
- k_2 \cos \theta_{2}) \delta(N(\sin
\theta_{\boldsymbol{k}} - \sin \theta_{1} - \sin
\theta_{2}))\nonumber\\ &\quad \times
\frac{|V_{12}^{\boldsymbol{k}}|^2}{\varDelta} \left( n_1
n_2 - n_{\boldsymbol{k}} n_1 - n_{\boldsymbol{k}} n_2
\right) k_1^2 \sin \theta_{1} k_2^2 \sin \theta_{2}
\,\mathrm{d} \theta_{1} \,\mathrm{d} k_1 \,\mathrm{d}
\theta_{2} \,\mathrm{d} k_2,
\end{align} \begin{align}\mathcal{J}_{\boldsymbol{k}} &= 8 {\rm \pi}\epsilon^2 \int
\delta(k_1 \cos \theta_{1} - k \cos \theta_{\boldsymbol{k}}
- k_2 \cos \theta_{2}) \delta(N(\sin \theta_{1} - \sin
\theta_{\boldsymbol{k}} - \sin \theta_{2}))\nonumber\\ &\quad\times
\frac{|V_{12}^{\boldsymbol{k}}|^2}{\varDelta} \left(
n_{\boldsymbol{k}} n_2 - n_1 n_{\boldsymbol{k}} - n_1 n_2
\right) k_1^2 \sin \theta_{1} k_2^2 \sin \theta_{2}
\,\mathrm{d} \theta_{1} \,\mathrm{d} k_1 \,\mathrm{d}
\theta_{2} \,\mathrm{d} k_2.
\end{align}
\begin{align}\mathcal{J}_{\boldsymbol{k}} &= 8 {\rm \pi}\epsilon^2 \int
\delta(k_1 \cos \theta_{1} - k \cos \theta_{\boldsymbol{k}}
- k_2 \cos \theta_{2}) \delta(N(\sin \theta_{1} - \sin
\theta_{\boldsymbol{k}} - \sin \theta_{2}))\nonumber\\ &\quad\times
\frac{|V_{12}^{\boldsymbol{k}}|^2}{\varDelta} \left(
n_{\boldsymbol{k}} n_2 - n_1 n_{\boldsymbol{k}} - n_1 n_2
\right) k_1^2 \sin \theta_{1} k_2^2 \sin \theta_{2}
\,\mathrm{d} \theta_{1} \,\mathrm{d} k_1 \,\mathrm{d}
\theta_{2} \,\mathrm{d} k_2.
\end{align} To go further, we need to parametrize the resonant manifold, corresponding to the set of wave vectors ![]() $(\boldsymbol {k}, \boldsymbol {k}_1, \boldsymbol {k}_2)$ satisfying the resonant conditions
$(\boldsymbol {k}, \boldsymbol {k}_1, \boldsymbol {k}_2)$ satisfying the resonant conditions
 \begin{equation} \begin{cases} \boldsymbol{k} = \boldsymbol{k}_1 + \boldsymbol{k}_2 \\ \omega_{\boldsymbol{k}} = \omega_{1} + \omega_{2} \end{cases} \quad \text{or} \quad \begin{cases} \boldsymbol{k}_1 = \boldsymbol{k} + \boldsymbol{k}_2 \\ \omega_{1} = \omega_{\boldsymbol{k}} + \omega_{2} \end{cases}. \end{equation}
\begin{equation} \begin{cases} \boldsymbol{k} = \boldsymbol{k}_1 + \boldsymbol{k}_2 \\ \omega_{\boldsymbol{k}} = \omega_{1} + \omega_{2} \end{cases} \quad \text{or} \quad \begin{cases} \boldsymbol{k}_1 = \boldsymbol{k} + \boldsymbol{k}_2 \\ \omega_{1} = \omega_{\boldsymbol{k}} + \omega_{2} \end{cases}. \end{equation}
It appears that it is relatively easy to find ![]() $(k_{2h}, k_{2z})$ as a function of
$(k_{2h}, k_{2z})$ as a function of ![]() $(k_h, k_z, k_{1h}, k_{1z})$. This leads to
$(k_h, k_z, k_{1h}, k_{1z})$. This leads to
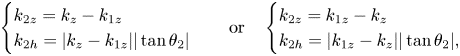 \begin{equation} \begin{cases} k_{2z} = k_z - k_{1z} \\ k_{2h} = |k_z - k_{1z}||\tan \theta_{2}| \end{cases} \quad \text{or} \quad \begin{cases} k_{2z} = k_{1z} - k_z \\ k_{2h} = |k_{1z} - k_z||\tan \theta_{2}| , \end{cases} \end{equation}
\begin{equation} \begin{cases} k_{2z} = k_z - k_{1z} \\ k_{2h} = |k_z - k_{1z}||\tan \theta_{2}| \end{cases} \quad \text{or} \quad \begin{cases} k_{2z} = k_{1z} - k_z \\ k_{2h} = |k_{1z} - k_z||\tan \theta_{2}| , \end{cases} \end{equation}
with ![]() $|\tan \theta _{2}| = {|\sin \theta _{\boldsymbol {k}} - \sin \theta _{1}|}/{\sqrt {1-(\sin \theta _{\boldsymbol {k}} - \sin \theta _{1})^2}}$ and
$|\tan \theta _{2}| = {|\sin \theta _{\boldsymbol {k}} - \sin \theta _{1}|}/{\sqrt {1-(\sin \theta _{\boldsymbol {k}} - \sin \theta _{1})^2}}$ and ![]() $\sin \theta _{1} = k_{1h}/k_1$. These solutions are valid if and only if
$\sin \theta _{1} = k_{1h}/k_1$. These solutions are valid if and only if
 \begin{equation} \begin{cases} \omega_{\boldsymbol{k}} \geq \omega_{1} \\ k_h \leq k_{1h} + k_{2h} \\ k_{1h} \leq k_{2h} + k_h \\ k_{2h} \leq k_h + k_{1h} \end{cases} \quad \text{or} \quad \begin{cases} \omega_{1} \geq \omega_{\boldsymbol{k}} \\ k_{1h} \leq k_h + k_{2h} \\ k_h \leq k_{2h} + k_{1h} \\ k_{2h} \leq k_{1h} + k_h , \end{cases} \end{equation}
\begin{equation} \begin{cases} \omega_{\boldsymbol{k}} \geq \omega_{1} \\ k_h \leq k_{1h} + k_{2h} \\ k_{1h} \leq k_{2h} + k_h \\ k_{2h} \leq k_h + k_{1h} \end{cases} \quad \text{or} \quad \begin{cases} \omega_{1} \geq \omega_{\boldsymbol{k}} \\ k_{1h} \leq k_h + k_{2h} \\ k_h \leq k_{2h} + k_{1h} \\ k_{2h} \leq k_{1h} + k_h , \end{cases} \end{equation}
otherwise there is no solution. We can use the ![]() $\delta$-Dirac function to perform integration over
$\delta$-Dirac function to perform integration over ![]() $k_{2h}$ and
$k_{2h}$ and ![]() $k_{2z}$ such that we finally obtain
$k_{2z}$ such that we finally obtain
where ![]() $\mathcal {D}_{\mathcal {I}}$ and
$\mathcal {D}_{\mathcal {I}}$ and ![]() $\mathcal {D}_{\mathcal {J}}$ are the integration domains of the resonant manifold given by conditions (3.28) detailed later and shown in figure 3. Note that it is possible to parameterize the resonant manifold with the variables
$\mathcal {D}_{\mathcal {J}}$ are the integration domains of the resonant manifold given by conditions (3.28) detailed later and shown in figure 3. Note that it is possible to parameterize the resonant manifold with the variables ![]() $(k_1,k_2)$ instead of
$(k_1,k_2)$ instead of ![]() $(k_1,\theta _{1})$. However, it requires solution of a polynomial equation of order 4 to find the angles
$(k_1,\theta _{1})$. However, it requires solution of a polynomial equation of order 4 to find the angles ![]() $(\theta _{1},\theta _{2})$. Despite the fact that it is mathematically possible, it leads to equations that are much more difficult to use than the one obtained when we parameterize the resonant manifold using
$(\theta _{1},\theta _{2})$. Despite the fact that it is mathematically possible, it leads to equations that are much more difficult to use than the one obtained when we parameterize the resonant manifold using ![]() $(k_1,\theta _{1})$.
$(k_1,\theta _{1})$.
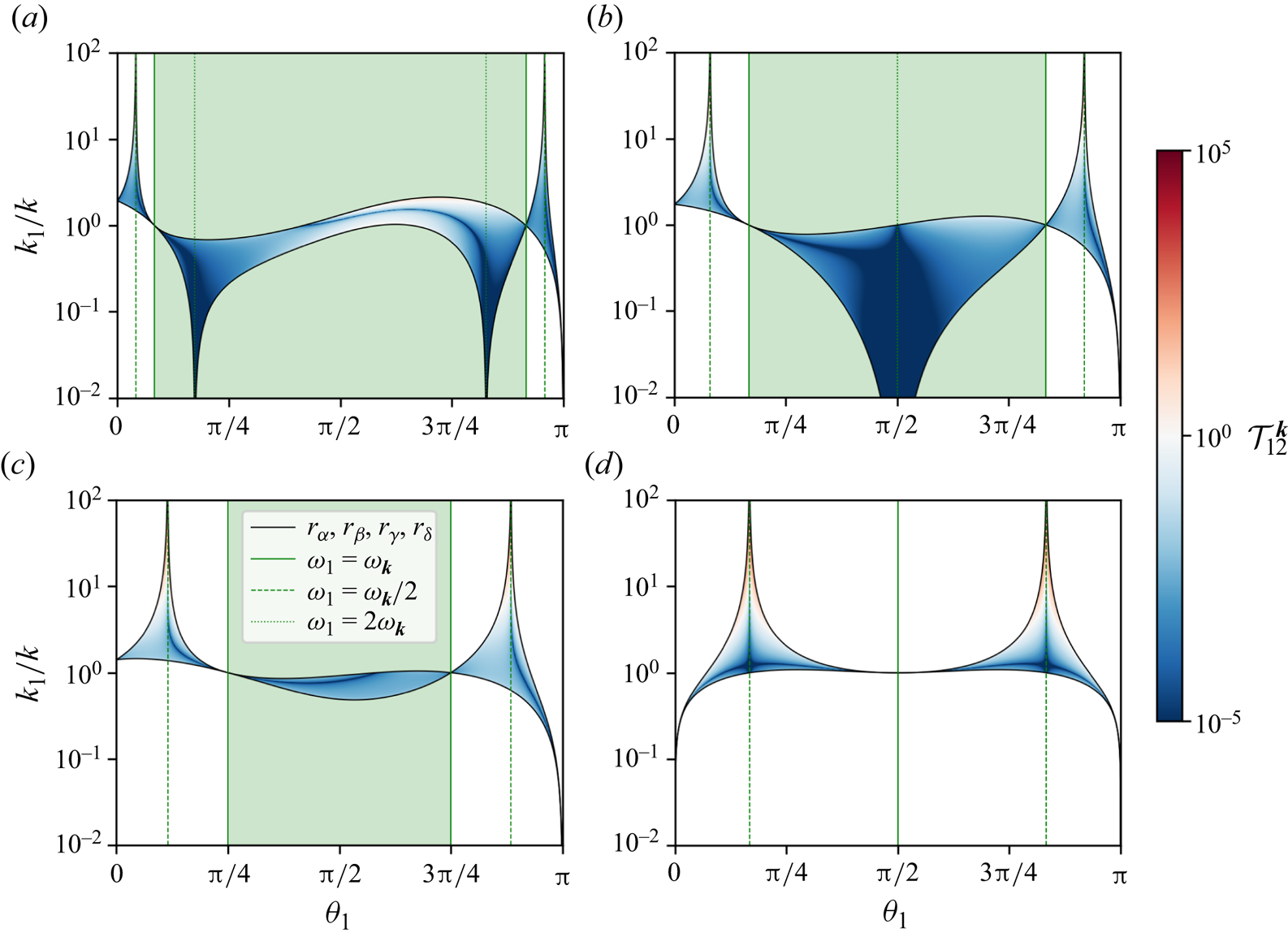
Figure 3. Transfer coefficient on the integration domain of the collisional integral for several ![]() $\theta _{\boldsymbol {k}} \in [0;{\rm \pi} /2]$: (a)
$\theta _{\boldsymbol {k}} \in [0;{\rm \pi} /2]$: (a) ![]() $\theta _{\boldsymbol {k}}={\rm \pi} /12$, (b)
$\theta _{\boldsymbol {k}}={\rm \pi} /12$, (b) ![]() $\theta _{\boldsymbol {k}}={\rm \pi} /6$, (c)
$\theta _{\boldsymbol {k}}={\rm \pi} /6$, (c) ![]() $\theta _{\boldsymbol {k}}={\rm \pi} /4$ and (d)
$\theta _{\boldsymbol {k}}={\rm \pi} /4$ and (d) ![]() $\theta _{\boldsymbol {k}}={\rm \pi} /2$. The borders of the domains are given by the critical lines
$\theta _{\boldsymbol {k}}={\rm \pi} /2$. The borders of the domains are given by the critical lines ![]() $r_{\alpha }$,
$r_{\alpha }$, ![]() $r_{\beta }$,
$r_{\beta }$, ![]() $r_{\gamma }$ and
$r_{\gamma }$ and ![]() $r_{\delta }$ ((3.31)–(3.34)). Here,
$r_{\delta }$ ((3.31)–(3.34)). Here, ![]() $\mathcal {D}_{\mathcal {I}}$ lies outside
$\mathcal {D}_{\mathcal {I}}$ lies outside ![]() $\omega _{1} = \omega _{\boldsymbol {k}}$ lines (white background), while
$\omega _{1} = \omega _{\boldsymbol {k}}$ lines (white background), while ![]() $\mathcal {D}_{\mathcal {J}}$ is contained inside
$\mathcal {D}_{\mathcal {J}}$ is contained inside ![]() $\omega _{1} = \omega _{\boldsymbol {k}}$ lines (green background).
$\omega _{1} = \omega _{\boldsymbol {k}}$ lines (green background).
For simplicity, in order to define analytically ![]() $\mathcal {D}_{\mathcal {I}}$ and
$\mathcal {D}_{\mathcal {I}}$ and ![]() $\mathcal {D}_{\mathcal {J}}$, we will assume that the wave-action spectrum is invariant under the transformation
$\mathcal {D}_{\mathcal {J}}$, we will assume that the wave-action spectrum is invariant under the transformation ![]() $k_z \rightarrow - k_z$, i.e.
$k_z \rightarrow - k_z$, i.e. ![]() $n(k_h, k_z) = n(k_h, -k_z)$. In this way, we can restrict the study of the collision integral to
$n(k_h, k_z) = n(k_h, -k_z)$. In this way, we can restrict the study of the collision integral to ![]() $k_z \geq 0$ (i.e.
$k_z \geq 0$ (i.e. ![]() $0 \leq \theta _{\boldsymbol {k}} \leq {\rm \pi}/2$). The study of the resonant surface when the wave-action spectrum does not have this symmetry requires consideration of the case with
$0 \leq \theta _{\boldsymbol {k}} \leq {\rm \pi}/2$). The study of the resonant surface when the wave-action spectrum does not have this symmetry requires consideration of the case with ![]() $k_z \leq 0$ (i.e.
$k_z \leq 0$ (i.e. ![]() ${\rm \pi} /2 \leq \theta _{\boldsymbol {k}} \leq {\rm \pi}$), which is longer but technically not more difficult. The borders of the integration domains
${\rm \pi} /2 \leq \theta _{\boldsymbol {k}} \leq {\rm \pi}$), which is longer but technically not more difficult. The borders of the integration domains ![]() $\mathcal {D}_{\mathcal {I}}$ and
$\mathcal {D}_{\mathcal {I}}$ and ![]() $\mathcal {D}_{\mathcal {J}}$ correspond to the zeros of
$\mathcal {D}_{\mathcal {J}}$ correspond to the zeros of ![]() $\varDelta$ given by (3.22). Note that the borders of the resonant manifold are attained for wave triads with co-linear horizontal projection, i.e. waves on the same vertical plane. They are easily obtained in the variable
$\varDelta$ given by (3.22). Note that the borders of the resonant manifold are attained for wave triads with co-linear horizontal projection, i.e. waves on the same vertical plane. They are easily obtained in the variable ![]() $k_1/k$ as a function of
$k_1/k$ as a function of ![]() $(\theta _{\boldsymbol {k}},\theta _{1})$. For each
$(\theta _{\boldsymbol {k}},\theta _{1})$. For each ![]() $(\theta _{\boldsymbol {k}},\theta _{1})$, the zeros of
$(\theta _{\boldsymbol {k}},\theta _{1})$, the zeros of ![]() $\varDelta$ are attained on two of the following lines:
$\varDelta$ are attained on two of the following lines:
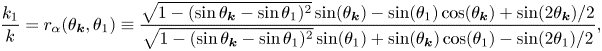 $$\begin{gather} \frac{k_1}{k} = r_{\alpha}(\theta_{\boldsymbol{k}}, \theta_{1}) \equiv \frac{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{\boldsymbol{k}})-\sin(\theta_{1})\cos(\theta_{\boldsymbol{k}})+\sin(2\theta_{\boldsymbol{k}})/2}{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{1})+\sin(\theta_{\boldsymbol{k}})\cos(\theta_{1})-\sin(2\theta_{1})/2}, \end{gather}$$
$$\begin{gather} \frac{k_1}{k} = r_{\alpha}(\theta_{\boldsymbol{k}}, \theta_{1}) \equiv \frac{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{\boldsymbol{k}})-\sin(\theta_{1})\cos(\theta_{\boldsymbol{k}})+\sin(2\theta_{\boldsymbol{k}})/2}{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{1})+\sin(\theta_{\boldsymbol{k}})\cos(\theta_{1})-\sin(2\theta_{1})/2}, \end{gather}$$ $$\begin{gather}\frac{k_1}{k} = r_{\beta}(\theta_{\boldsymbol{k}}, \theta_{1}) \equiv \frac{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{\boldsymbol{k}})+\sin(\theta_{1})\cos(\theta_{\boldsymbol{k}})-\sin(2\theta_{\boldsymbol{k}})/2}{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{1})-\sin(\theta_{\boldsymbol{k}})\cos(\theta_{1})+\sin(2\theta_{1})/2}, \end{gather}$$
$$\begin{gather}\frac{k_1}{k} = r_{\beta}(\theta_{\boldsymbol{k}}, \theta_{1}) \equiv \frac{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{\boldsymbol{k}})+\sin(\theta_{1})\cos(\theta_{\boldsymbol{k}})-\sin(2\theta_{\boldsymbol{k}})/2}{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{1})-\sin(\theta_{\boldsymbol{k}})\cos(\theta_{1})+\sin(2\theta_{1})/2}, \end{gather}$$ $$\begin{gather}\frac{k_1}{k} = r_{\gamma}(\theta_{\boldsymbol{k}}, \theta_{1}) \equiv \frac{-\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{\boldsymbol{k}})-\sin(\theta_{1})\cos(\theta_{\boldsymbol{k}})+\sin(2\theta_{\boldsymbol{k}})/2}{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{1})+\sin(\theta_{\boldsymbol{k}})\cos(\theta_{1})-\sin(2\theta_{1})/2}, \end{gather}$$
$$\begin{gather}\frac{k_1}{k} = r_{\gamma}(\theta_{\boldsymbol{k}}, \theta_{1}) \equiv \frac{-\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{\boldsymbol{k}})-\sin(\theta_{1})\cos(\theta_{\boldsymbol{k}})+\sin(2\theta_{\boldsymbol{k}})/2}{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{1})+\sin(\theta_{\boldsymbol{k}})\cos(\theta_{1})-\sin(2\theta_{1})/2}, \end{gather}$$ $$\begin{gather}\frac{k_1}{k} = r_{\delta}(\theta_{\boldsymbol{k}}, \theta_{1}) \equiv \frac{-\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{\boldsymbol{k}})+\sin(\theta_{1})\cos(\theta_{\boldsymbol{k}})-\sin(2\theta_{\boldsymbol{k}})/2}{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{1})-\sin(\theta_{\boldsymbol{k}})\cos(\theta_{1})+\sin(2\theta_{1})/2}, \end{gather}$$
$$\begin{gather}\frac{k_1}{k} = r_{\delta}(\theta_{\boldsymbol{k}}, \theta_{1}) \equiv \frac{-\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{\boldsymbol{k}})+\sin(\theta_{1})\cos(\theta_{\boldsymbol{k}})-\sin(2\theta_{\boldsymbol{k}})/2}{\sqrt{1-(\sin \theta_{\boldsymbol{k}} - \sin \theta_{1})^2}\sin(\theta_{1})-\sin(\theta_{\boldsymbol{k}})\cos(\theta_{1})+\sin(2\theta_{1})/2}, \end{gather}$$
leading to the subdomains of ![]() $\mathcal {D}_{\mathcal {I}}$ and
$\mathcal {D}_{\mathcal {I}}$ and ![]() $\mathcal {D}_{\mathcal {J}}$ that are listed in table 1. It is worth mentioning that the description of the resonant manifold of internal waves (accounting for rotation) in the
$\mathcal {D}_{\mathcal {J}}$ that are listed in table 1. It is worth mentioning that the description of the resonant manifold of internal waves (accounting for rotation) in the ![]() $(k_1/k, \theta _{\boldsymbol {k}}, \theta _{1})$ variables is available in Olbers (Reference Olbers1974) (see § 4 of this reference).
$(k_1/k, \theta _{\boldsymbol {k}}, \theta _{1})$ variables is available in Olbers (Reference Olbers1974) (see § 4 of this reference).
Table 1. Subdomains of the resonant manifolds ![]() $\mathcal {D}_{\mathcal {I}}$ and
$\mathcal {D}_{\mathcal {I}}$ and ![]() $\mathcal {D}_{\mathcal {J}}$ for
$\mathcal {D}_{\mathcal {J}}$ for ![]() $\theta _{\boldsymbol {k}} \in [0;{\rm \pi} /2]$.
$\theta _{\boldsymbol {k}} \in [0;{\rm \pi} /2]$.
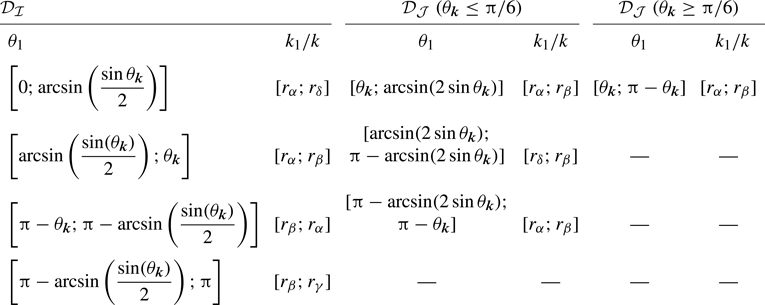
In figure 3, we represent the transfer coefficient ![]() $\mathcal {T}_{12}^{\boldsymbol {k}} \equiv k_1^2 \sin \theta _{1} k_2^2 \sin \theta _{2} |V_{12}^{\boldsymbol {k}}|^2 / (\cos ^2 \theta _{2} \varDelta )$ on the integration domains
$\mathcal {T}_{12}^{\boldsymbol {k}} \equiv k_1^2 \sin \theta _{1} k_2^2 \sin \theta _{2} |V_{12}^{\boldsymbol {k}}|^2 / (\cos ^2 \theta _{2} \varDelta )$ on the integration domains ![]() $\mathcal {D}_{\mathcal {I}}$ and
$\mathcal {D}_{\mathcal {I}}$ and ![]() $\mathcal {D}_{\mathcal {J}}$. Here,
$\mathcal {D}_{\mathcal {J}}$. Here, ![]() $\mathcal {T}_{12}^{\boldsymbol {k}}$ measures the strength of the interaction of the triad ((3.29)–(3.30)), which is important information for studying the evolution of IGWs. As can be expected from earlier studies (McComas & Bretherton Reference McComas and Bretherton1977; Müller et al. Reference Müller, Holloway, Henyey and Pomphrey1986; Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Eden, Pollmann & Olbers Reference Eden, Pollmann and Olbers2019; Olbers, Pollmann & Eden Reference Olbers, Pollmann and Eden2020; Lanchon & Cortet Reference Lanchon and Cortet2023), the transfer coefficient is important for triads with large scale separation, i.e. when
$\mathcal {T}_{12}^{\boldsymbol {k}}$ measures the strength of the interaction of the triad ((3.29)–(3.30)), which is important information for studying the evolution of IGWs. As can be expected from earlier studies (McComas & Bretherton Reference McComas and Bretherton1977; Müller et al. Reference Müller, Holloway, Henyey and Pomphrey1986; Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Eden, Pollmann & Olbers Reference Eden, Pollmann and Olbers2019; Olbers, Pollmann & Eden Reference Olbers, Pollmann and Eden2020; Lanchon & Cortet Reference Lanchon and Cortet2023), the transfer coefficient is important for triads with large scale separation, i.e. when ![]() $k_1$ or
$k_1$ or ![]() $k_2 \gg k$. The transfer coefficient is also large for triads with
$k_2 \gg k$. The transfer coefficient is also large for triads with ![]() $k \sim k_1 \sim k_2$ at the border of the domain, corresponding to triads contained in a vertical plane. It is in line with Dematteis & Lvov (Reference Dematteis and Lvov2021), who showed that the dominant contribution to the collision integral for the steady-state spectra, in the hydrostatic limit, is due to the horizontally co-linear wave triads. It has also been shown that local interactions correspond to an important part of the energy transfers for the Garrett–Munk spectrum (Wu & Pan Reference Wu and Pan2023).
$k \sim k_1 \sim k_2$ at the border of the domain, corresponding to triads contained in a vertical plane. It is in line with Dematteis & Lvov (Reference Dematteis and Lvov2021), who showed that the dominant contribution to the collision integral for the steady-state spectra, in the hydrostatic limit, is due to the horizontally co-linear wave triads. It has also been shown that local interactions correspond to an important part of the energy transfers for the Garrett–Munk spectrum (Wu & Pan Reference Wu and Pan2023).
3.4. Hydrostatic limit
In strongly stratified flows, the energy tends to concentrate in modes with wave vectors such that the vertical component is much larger than the horizontal one. It is therefore worth considering the almost vertical propagation hypothesis (or hydrostatic limit) with ![]() $|k_z| \gg k_h$, and so
$|k_z| \gg k_h$, and so ![]() $\omega _{\boldsymbol {k}} = N k_h/k \simeq N k_h/|k_z|$. In that limit, our kinetic equation is equivalent to other kinetic equations of IGW turbulence (Müller & Olbers Reference Müller and Olbers1975; Caillol & Zeitlin Reference Caillol and Zeitlin2000; Lvov & Tabak Reference Lvov and Tabak2001), as shown in the review of Lvov et al. (Reference Lvov, Polzin and Yokoyama2012). We have checked that our interaction coefficients are equal to the one of Lvov & Tabak (Reference Lvov and Tabak2001) up to machine precision in the hydrostatic limit, when evaluated on the resonant manifold. In the hydrostatic limit, we can find stationary, axisymmetric, bi-homogeneous solutions
$\omega _{\boldsymbol {k}} = N k_h/k \simeq N k_h/|k_z|$. In that limit, our kinetic equation is equivalent to other kinetic equations of IGW turbulence (Müller & Olbers Reference Müller and Olbers1975; Caillol & Zeitlin Reference Caillol and Zeitlin2000; Lvov & Tabak Reference Lvov and Tabak2001), as shown in the review of Lvov et al. (Reference Lvov, Polzin and Yokoyama2012). We have checked that our interaction coefficients are equal to the one of Lvov & Tabak (Reference Lvov and Tabak2001) up to machine precision in the hydrostatic limit, when evaluated on the resonant manifold. In the hydrostatic limit, we can find stationary, axisymmetric, bi-homogeneous solutions ![]() $n_{\boldsymbol {k}} = n(k_h,k_z) \propto k_h^{\nu _h} |k_z|^{\nu _z}$ to the wave-kinetic equation. This theoretical and numerical work has already been achieved in earlier studies (Pelinovsky & Raevsky Reference Pelinovsky and Raevsky1977; Caillol & Zeitlin Reference Caillol and Zeitlin2000; Lvov & Tabak Reference Lvov and Tabak2001; Lvov et al. Reference Lvov, Polzin and Tabak2004, Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021), so we will not repeat all the computations here. Instead, we show that the KZ spectrum can be obtained without involving resonance condition in frequencies.
$n_{\boldsymbol {k}} = n(k_h,k_z) \propto k_h^{\nu _h} |k_z|^{\nu _z}$ to the wave-kinetic equation. This theoretical and numerical work has already been achieved in earlier studies (Pelinovsky & Raevsky Reference Pelinovsky and Raevsky1977; Caillol & Zeitlin Reference Caillol and Zeitlin2000; Lvov & Tabak Reference Lvov and Tabak2001; Lvov et al. Reference Lvov, Polzin and Tabak2004, Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021), so we will not repeat all the computations here. Instead, we show that the KZ spectrum can be obtained without involving resonance condition in frequencies.
In the hydrostatic limit, we have the following simplifications:
and similar relations after permutations of wave vectors. Note that the scalar products of horizontal wave vectors (e.g. ![]() $\boldsymbol {k}_{1h} \boldsymbol {\cdot } \boldsymbol {k}_{2h}$) are determined by the resonance condition for horizontal wave vectors, and are only functions of
$\boldsymbol {k}_{1h} \boldsymbol {\cdot } \boldsymbol {k}_{2h}$) are determined by the resonance condition for horizontal wave vectors, and are only functions of ![]() $(k_h,k_{1h},k_{2h})$. Outside the hydrostatic limit, the wave frequency and interaction coefficients are homogeneous in wave-vector amplitudes
$(k_h,k_{1h},k_{2h})$. Outside the hydrostatic limit, the wave frequency and interaction coefficients are homogeneous in wave-vector amplitudes ![]() $(k,k_1,k_2)$, but not in
$(k,k_1,k_2)$, but not in ![]() $(k_h,k_{1h},k_{2h})$ and
$(k_h,k_{1h},k_{2h})$ and ![]() $(|k_z|,|k_{1z}|,|k_{2z}|)$ separately. Contrarily, in the hydrostatic limit, the wave frequency and interaction coefficients are bi-homogeneous, i.e. are homogeneous in
$(|k_z|,|k_{1z}|,|k_{2z}|)$ separately. Contrarily, in the hydrostatic limit, the wave frequency and interaction coefficients are bi-homogeneous, i.e. are homogeneous in ![]() $(k_h,k_{1h},k_{2h})$ and
$(k_h,k_{1h},k_{2h})$ and ![]() $(|k_z|,|k_{1z}|,|k_{2z}|)$ separately. More precisely, the transformation
$(|k_z|,|k_{1z}|,|k_{2z}|)$ separately. More precisely, the transformation ![]() $(k_h,k_{1h},k_{2h}) \rightarrow \mu _h (k_h,k_{1h},k_{2h})$,
$(k_h,k_{1h},k_{2h}) \rightarrow \mu _h (k_h,k_{1h},k_{2h})$, ![]() $(k_z,k_{1z},k_{2z}) \rightarrow \mu _z (k_z,k_{1z},k_{2z})$ changes the frequency and interaction coefficients in the following way:
$(k_z,k_{1z},k_{2z}) \rightarrow \mu _z (k_z,k_{1z},k_{2z})$ changes the frequency and interaction coefficients in the following way:
where we have used the notation of Balk & Nazarenko (Reference Balk and Nazarenko1990) ![]() $\boldsymbol {\mu }^{\boldsymbol {\alpha }} \equiv \mu _h^{\alpha _h} \mu _z^{\alpha _z}$, with
$\boldsymbol {\mu }^{\boldsymbol {\alpha }} \equiv \mu _h^{\alpha _h} \mu _z^{\alpha _z}$, with ![]() $\boldsymbol {\alpha } = (1,-1)$ and
$\boldsymbol {\alpha } = (1,-1)$ and ![]() $\boldsymbol {\beta } = ( \tfrac {3}{2}, -\tfrac {1}{2} )$. The homogeneity degrees inside and outside the hydrostatic limit are linked by
$\boldsymbol {\beta } = ( \tfrac {3}{2}, -\tfrac {1}{2} )$. The homogeneity degrees inside and outside the hydrostatic limit are linked by ![]() $\alpha _h+\alpha _z=\alpha =0$ and
$\alpha _h+\alpha _z=\alpha =0$ and ![]() $\beta _h+\beta _z=\beta =1$.
$\beta _h+\beta _z=\beta =1$.
We now perform the Zakharov-Kuznetsov transformation (Kuznetsov Reference Kuznetsov1972) for bi-homogenous spectra
to the integral with ![]() $\mathcal {Q}_{\boldsymbol{k} 2}^{1}$, and a similar transformation for the integral with
$\mathcal {Q}_{\boldsymbol{k} 2}^{1}$, and a similar transformation for the integral with ![]() $\mathcal {Q}_{\boldsymbol{k} 1}^{2}$ in the wave-kinetic equation (3.4). After the ZK transformation (3.37a,b), the collision integral becomes
$\mathcal {Q}_{\boldsymbol{k} 1}^{2}$ in the wave-kinetic equation (3.4). After the ZK transformation (3.37a,b), the collision integral becomes
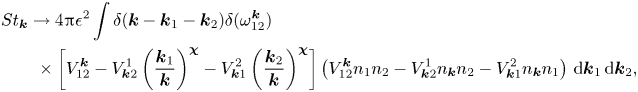 \begin{align} &St_{\boldsymbol{k}} \rightarrow 4 {\rm \pi}\epsilon^2 \int \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2) \delta(\omega_{12}^{\boldsymbol{k}}) \nonumber\\ &\qquad \times \left[ V_{12}^{\boldsymbol{k}} - V_{\boldsymbol{k}2}^{1} \left( \frac{\boldsymbol{k}_1}{\boldsymbol{k}} \right)^{\boldsymbol{\chi}} - V_{\boldsymbol{k}1}^{2} \left( \frac{\boldsymbol{k}_2}{\boldsymbol{k}} \right)^{\boldsymbol{\chi}} \right] \left( V_{12}^{\boldsymbol{k}} n_1 n_2 - V_{\boldsymbol{k}2}^{1} n_{\boldsymbol{k}} n_2 - V_{\boldsymbol{k}1}^{2} n_{\boldsymbol{k}} n_1 \right) \,\mathrm{d} \boldsymbol{k}_1 \,\mathrm{d} \boldsymbol{k}_2 , \end{align}
\begin{align} &St_{\boldsymbol{k}} \rightarrow 4 {\rm \pi}\epsilon^2 \int \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2) \delta(\omega_{12}^{\boldsymbol{k}}) \nonumber\\ &\qquad \times \left[ V_{12}^{\boldsymbol{k}} - V_{\boldsymbol{k}2}^{1} \left( \frac{\boldsymbol{k}_1}{\boldsymbol{k}} \right)^{\boldsymbol{\chi}} - V_{\boldsymbol{k}1}^{2} \left( \frac{\boldsymbol{k}_2}{\boldsymbol{k}} \right)^{\boldsymbol{\chi}} \right] \left( V_{12}^{\boldsymbol{k}} n_1 n_2 - V_{\boldsymbol{k}2}^{1} n_{\boldsymbol{k}} n_2 - V_{\boldsymbol{k}1}^{2} n_{\boldsymbol{k}} n_1 \right) \,\mathrm{d} \boldsymbol{k}_1 \,\mathrm{d} \boldsymbol{k}_2 , \end{align}
with ![]() $\boldsymbol {d} = (2,1)$ and
$\boldsymbol {d} = (2,1)$ and ![]() $\boldsymbol {\chi } = \boldsymbol {\alpha } - 2 \boldsymbol {\beta } - 2 \boldsymbol {\nu } - 2 \boldsymbol {d}$. The integrand in (3.39) is zero when
$\boldsymbol {\chi } = \boldsymbol {\alpha } - 2 \boldsymbol {\beta } - 2 \boldsymbol {\nu } - 2 \boldsymbol {d}$. The integrand in (3.39) is zero when ![]() $-\boldsymbol {\nu } = \boldsymbol {\alpha }$ (
$-\boldsymbol {\nu } = \boldsymbol {\alpha }$ (![]() $n_{\boldsymbol {k}} \propto 1/\omega _{\boldsymbol {k}}$), which corresponds to the RJ spectrum, and when
$n_{\boldsymbol {k}} \propto 1/\omega _{\boldsymbol {k}}$), which corresponds to the RJ spectrum, and when ![]() $\boldsymbol {\chi } = \boldsymbol {\alpha }$, which leads to the KZ spectrum
$\boldsymbol {\chi } = \boldsymbol {\alpha }$, which leads to the KZ spectrum ![]() $n_{\boldsymbol {k}} \propto k_h^{-7/2} |k_z|^{-1/2}$. Interestingly, we obtain the RJ and the KZ spectra by using the symmetry of the interaction coefficients (2.12a,b), and not the resonance on frequencies, which is unusual in WWT theory. As said in the introduction, the same theoretical spectrum was first obtained by Pelinovsky & Raevsky (Reference Pelinovsky and Raevsky1977), and later by Caillol & Zeitlin (Reference Caillol and Zeitlin2000) and Lvov & Tabak (Reference Lvov and Tabak2001) using different formalisms. Yet, the ZK transformation (3.38a,b) is a non-identity transformation that takes the limit of zero wavenumbers to infinity and vice versa, which may lead to the cancellation of oppositely signed divergences. If the original collision integral converges and is equal to zero, then the found spectrum is indeed a valid solution, in which case the spectrum is called local. If not, then the spectrum in question is a spurious solution; it is called a non-local spectrum (Nazarenko Reference Nazarenko2011) and is not physically realizable. It turned out that the KZ (or PR) spectrum is non-local (Caillol & Zeitlin Reference Caillol and Zeitlin2000).
$n_{\boldsymbol {k}} \propto k_h^{-7/2} |k_z|^{-1/2}$. Interestingly, we obtain the RJ and the KZ spectra by using the symmetry of the interaction coefficients (2.12a,b), and not the resonance on frequencies, which is unusual in WWT theory. As said in the introduction, the same theoretical spectrum was first obtained by Pelinovsky & Raevsky (Reference Pelinovsky and Raevsky1977), and later by Caillol & Zeitlin (Reference Caillol and Zeitlin2000) and Lvov & Tabak (Reference Lvov and Tabak2001) using different formalisms. Yet, the ZK transformation (3.38a,b) is a non-identity transformation that takes the limit of zero wavenumbers to infinity and vice versa, which may lead to the cancellation of oppositely signed divergences. If the original collision integral converges and is equal to zero, then the found spectrum is indeed a valid solution, in which case the spectrum is called local. If not, then the spectrum in question is a spurious solution; it is called a non-local spectrum (Nazarenko Reference Nazarenko2011) and is not physically realizable. It turned out that the KZ (or PR) spectrum is non-local (Caillol & Zeitlin Reference Caillol and Zeitlin2000).
The collision integral is expected to have other zeros. This situation is typical for anisotropic media (Kuznetsov Reference Kuznetsov1972; Balk & Nazarenko Reference Balk and Nazarenko1990; Lvov et al. Reference Lvov, Polzin and Tabak2004). To find these spectra, we need to compute the collision integral to find its zeros in the ![]() $(\nu _h,\nu _z)$ plane. It is important to note that the integrand in the collision integral can diverge if
$(\nu _h,\nu _z)$ plane. It is important to note that the integrand in the collision integral can diverge if ![]() $k_{1h}$ or
$k_{1h}$ or ![]() $k_{2h} \rightarrow 0$ which corresponds to infrared (IR) divergence, and when
$k_{2h} \rightarrow 0$ which corresponds to infrared (IR) divergence, and when ![]() $k_{1h}, k_{2h} \rightarrow \infty$ which correspond to ultraviolet (UV) divergence. Depending on
$k_{1h}, k_{2h} \rightarrow \infty$ which correspond to ultraviolet (UV) divergence. Depending on ![]() $(\nu _h,\nu _z)$, the divergences can be integrable (in which case the spectrum is local), or non-integrable (in which case the spectrum is non-local). To identify these divergences, we need to analyse the terms of the collision integral and see for which values of
$(\nu _h,\nu _z)$, the divergences can be integrable (in which case the spectrum is local), or non-integrable (in which case the spectrum is non-local). To identify these divergences, we need to analyse the terms of the collision integral and see for which values of ![]() $(\nu _h,\nu _z)$ they lead to non-integrable divergences. The locality conditions have been obtained by Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010), and it was shown that another steady-state solution exists due to the opposite signs of IR and UV divergences. More precisely, the collision integral converges only on the segment
$(\nu _h,\nu _z)$ they lead to non-integrable divergences. The locality conditions have been obtained by Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010), and it was shown that another steady-state solution exists due to the opposite signs of IR and UV divergences. More precisely, the collision integral converges only on the segment ![]() $\nu _z = 0$,
$\nu _z = 0$, ![]() $-4 < \nu _h < -3$ and the steady-state spectrum
$-4 < \nu _h < -3$ and the steady-state spectrum ![]() $n_{\boldsymbol {k}} \propto k_h^{-3.69}$ has been obtained by finding the zero of the collision integral on this segment numerically (Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021). Yet, any spectrum with
$n_{\boldsymbol {k}} \propto k_h^{-3.69}$ has been obtained by finding the zero of the collision integral on this segment numerically (Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021). Yet, any spectrum with ![]() $\nu _z \neq 0$ around that solution would lead to a divergent collision integral. It means that the collision integral is not differentiable with respect to
$\nu _z \neq 0$ around that solution would lead to a divergent collision integral. It means that the collision integral is not differentiable with respect to ![]() $\nu _z$ and
$\nu _z$ and ![]() $\nu _h$ for spectra with
$\nu _h$ for spectra with ![]() $\nu _z=0$ and, therefore, the energy flux integrals are divergent (see Zakharov et al. Reference Zakharov, L'vov and Falkovich1992, § 3.32). This rules out realizability of these spectra. Since our formalism is equivalent to Lvov & Tabak (Reference Lvov and Tabak2001) in the hydrostatic limit, the same results are expected.
$\nu _z=0$ and, therefore, the energy flux integrals are divergent (see Zakharov et al. Reference Zakharov, L'vov and Falkovich1992, § 3.32). This rules out realizability of these spectra. Since our formalism is equivalent to Lvov & Tabak (Reference Lvov and Tabak2001) in the hydrostatic limit, the same results are expected.
4. Discussion and conclusions
We have presented a new derivation of the kinetic equation describing the weak internal gravity wave turbulence using poloidal–toroidal-shear decomposition (Craya Reference Craya1957; Herring Reference Herring1974; Godeferd et al. Reference Godeferd, Delache and Cambon2010). This decomposition is particularly well adapted to the problem because it offers a complete basis of the flow modes, uses standard Eulerian coordinates and the poloidal velocity is the kinetic part of the wave mode coupled to the buoyancy. The resulting kinetic equation has an advantage of holding in the non-hydrostatic case. It is equivalent to the one obtained by Caillol & Zeitlin (Reference Caillol and Zeitlin2000), but is considerably more compact than the latter. The interaction coefficients satisfy symmetries (Remmel & Smith Reference Remmel and Smith2009) that impose energy conservation both at the wave-action equation level, and at the kinetic equation level. It results that energy conservation in the kinetic equation can be demonstrated without using the resonance condition in frequencies, which is unusual in WWT theory. Similarly, we show that Rayleigh–Jeans and KZ spectra can be obtained using this symmetry, without involving resonance condition in frequencies. Adapting the computations of Shavit et al. (Reference Shavit, Bühler and Shatah2024), we obtain a stationarity condition for a scale-invariant spectra ![]() $n_{\boldsymbol {k}} = k^{\nu } f(\theta _{\boldsymbol {k}},\varphi _{\boldsymbol {k}})$, and show that
$n_{\boldsymbol {k}} = k^{\nu } f(\theta _{\boldsymbol {k}},\varphi _{\boldsymbol {k}})$, and show that ![]() $\nu =-4$ is a good candidate, in reasonably good agreement with known theoretical results and oceanic measurements (Lvov et al. Reference Lvov, Polzin and Tabak2004). It is worth mentioning that, in the hydrostatic limit, these spectra are known to lead to divergences of the collisional integral (Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021). Validity of a scale-invariant spectra of the form
$\nu =-4$ is a good candidate, in reasonably good agreement with known theoretical results and oceanic measurements (Lvov et al. Reference Lvov, Polzin and Tabak2004). It is worth mentioning that, in the hydrostatic limit, these spectra are known to lead to divergences of the collisional integral (Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Dematteis & Lvov Reference Dematteis and Lvov2021). Validity of a scale-invariant spectra of the form ![]() $n_{\boldsymbol {k}} = k^{-4} f(\theta _{\boldsymbol {k}},\varphi _{\boldsymbol {k}})$ remains to be checked. We have shown that the interaction coefficients are fully symmetric with respect to permutation of wave vectors on the resonant manifold, even outside the hydrostatic limit. It follows that the kinetic equation has a canonical structure, despite the fact that the original equation does not have a canonical Hamiltonian structure. Namely, the kinetic equation reads
$n_{\boldsymbol {k}} = k^{-4} f(\theta _{\boldsymbol {k}},\varphi _{\boldsymbol {k}})$ remains to be checked. We have shown that the interaction coefficients are fully symmetric with respect to permutation of wave vectors on the resonant manifold, even outside the hydrostatic limit. It follows that the kinetic equation has a canonical structure, despite the fact that the original equation does not have a canonical Hamiltonian structure. Namely, the kinetic equation reads
with ![]() $\omega _{\boldsymbol {k}} = N \sin \theta _{\boldsymbol {k}}$, and interaction coefficients
$\omega _{\boldsymbol {k}} = N \sin \theta _{\boldsymbol {k}}$, and interaction coefficients ![]() $V_{12}^{\boldsymbol {k}}$ given by (2.11). We have parametrized the resonant manifold, allowing us to give a simplified version of the kinetic equation for axisymmetric spectra. We have computed numerically the transfer coefficient, quantifying the strength of the interaction, for all triads of the resonant manifold. Consistently with earlier studies, we find that interactions corresponding to large scale separation (McComas & Bretherton Reference McComas and Bretherton1977; Müller et al. Reference Müller, Holloway, Henyey and Pomphrey1986; Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Eden et al. Reference Eden, Pollmann and Olbers2019; Olbers et al. Reference Olbers, Pollmann and Eden2020; Lanchon & Cortet Reference Lanchon and Cortet2023) and local interactions (Dematteis & Lvov Reference Dematteis and Lvov2021; Wu & Pan Reference Wu and Pan2023) both play an important role on the dynamics of IGW turbulence. In the hydrostatic limit, our kinetic equation is equivalent to many other formalisms (Lvov & Tabak Reference Lvov and Tabak2001; Lvov et al. Reference Lvov, Polzin and Yokoyama2012) so we refer the reader to the numerous studies available in the literature, in particular Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010) and Dematteis & Lvov (Reference Dematteis and Lvov2021).
$V_{12}^{\boldsymbol {k}}$ given by (2.11). We have parametrized the resonant manifold, allowing us to give a simplified version of the kinetic equation for axisymmetric spectra. We have computed numerically the transfer coefficient, quantifying the strength of the interaction, for all triads of the resonant manifold. Consistently with earlier studies, we find that interactions corresponding to large scale separation (McComas & Bretherton Reference McComas and Bretherton1977; Müller et al. Reference Müller, Holloway, Henyey and Pomphrey1986; Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Eden et al. Reference Eden, Pollmann and Olbers2019; Olbers et al. Reference Olbers, Pollmann and Eden2020; Lanchon & Cortet Reference Lanchon and Cortet2023) and local interactions (Dematteis & Lvov Reference Dematteis and Lvov2021; Wu & Pan Reference Wu and Pan2023) both play an important role on the dynamics of IGW turbulence. In the hydrostatic limit, our kinetic equation is equivalent to many other formalisms (Lvov & Tabak Reference Lvov and Tabak2001; Lvov et al. Reference Lvov, Polzin and Yokoyama2012) so we refer the reader to the numerous studies available in the literature, in particular Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010) and Dematteis & Lvov (Reference Dematteis and Lvov2021).
Supplementary material
We provide the Mathematica script allowing us to prove analytically equation (3.16), and a Jupyter notebook that allows us to check the symmetry of the interaction coefficients on the resonant manifold by direct numerical computations.
Supplementary material is available at https://doi.org/10.1017/jfm.2024.802.
Acknowledgements
We thank J. Shatah, O. Bühler, M. Shavit and M. Onorato for fruitful discussions. We are grateful to three referees whose remarks helped to significantly improve this work.
Funding
This work was supported by the Simons Foundation through grant no. 651471 GK and no. 651461 PPC.
Declaration of interests
The authors report no conflict of interest.
Author contributions
V.L., G.K. and S.N. have performed the analytical derivations. All the authors contributed to prove the canonical form of the kinetic equation and contributed to write the paper.
Data availability statement
No data are associated with this work.
Appendix A. Derivation of the wave-kinetic equation
Here, we derive the wave-kinetic equation ((3.4)–(3.6)) starting from the interaction representation variable equation (3.2). Firstly, we remark that the last term will lead to interaction between modes satisfying ![]() $\omega _{\boldsymbol {k}} + \omega _{1} + \omega _{2} = 0$ after taking the limit
$\omega _{\boldsymbol {k}} + \omega _{1} + \omega _{2} = 0$ after taking the limit ![]() $\epsilon \rightarrow 0$. Since
$\epsilon \rightarrow 0$. Since ![]() $\omega _{\boldsymbol {k}} \geq 0$, this term will therefore correspond to interactions between shear modes, which are not taken into account here. For this reason, we do not need to consider the last term of equation (3.2) to obtain the wave-kinetic equation. The next step is to consider an intermediate (between linear and nonlinear) time
$\omega _{\boldsymbol {k}} \geq 0$, this term will therefore correspond to interactions between shear modes, which are not taken into account here. For this reason, we do not need to consider the last term of equation (3.2) to obtain the wave-kinetic equation. The next step is to consider an intermediate (between linear and nonlinear) time ![]() $T$,
$T$, ![]() ${2{\rm \pi} }/{\omega _{\boldsymbol {k}}} \ll T = {2{\rm \pi} }/{\epsilon \omega _{\boldsymbol {k}}} \ll {2{\rm \pi} }/{\epsilon ^2 \omega _{\boldsymbol {k}}}$, use an expansion in
${2{\rm \pi} }/{\omega _{\boldsymbol {k}}} \ll T = {2{\rm \pi} }/{\epsilon \omega _{\boldsymbol {k}}} \ll {2{\rm \pi} }/{\epsilon ^2 \omega _{\boldsymbol {k}}}$, use an expansion in ![]() $\epsilon$ up to second order,
$\epsilon$ up to second order, ![]() $c_{\boldsymbol {k}}(T) = c_{\boldsymbol {k}}^{(0)} + \epsilon c_{\boldsymbol {k}}^{(1)} + \epsilon ^2 c_{\boldsymbol {k}}^{(2)} + O(\epsilon ^3)$ and obtain the following expression for the expansion of
$c_{\boldsymbol {k}}(T) = c_{\boldsymbol {k}}^{(0)} + \epsilon c_{\boldsymbol {k}}^{(1)} + \epsilon ^2 c_{\boldsymbol {k}}^{(2)} + O(\epsilon ^3)$ and obtain the following expression for the expansion of ![]() $c_{\boldsymbol {k}}(T)$:
$c_{\boldsymbol {k}}(T)$:
 \begin{align} c_{\boldsymbol{k}}^{(2)}(T) &={-} 2 \sum_{1,2,3,4} V_{12}^{\boldsymbol{k}} \delta_{12}^{\boldsymbol{k}} \left[V_{34}^2 \delta_{34}^2 c_1^{(0)} c_3^{(0)} c_4^{(0)} \varLambda_T(\omega_{34}^2, \omega_{12}^{\boldsymbol{k}}) \right.\nonumber\\ &\left.\quad +\, 2 V_{34}^2 \delta_{24}^3 c_1^{(0)} c_3^{(0)} c_4^{(0)*} \varLambda_T(-\omega_{24}^3, \omega_{12}^{\boldsymbol{k}}) \right]\nonumber\\ & \quad - 2 \sum_{1,2,3,4} V_{12}^{\boldsymbol{k}} \delta_{\boldsymbol{k}2}^1 \left[ V_{34}^1 \delta_{34}^1 c_2^{(0)*} c_3^{(0)} c_4^{(0)} \varLambda_T(\omega_{34}^1, -\omega_{\boldsymbol{k}2}^{1}) \right.\nonumber\\ &\left. \quad +\, 2 V_{34}^1 \delta_{14}^3 c_2^{(0)*} c_3^{(0)} c_4^{(0)*} \varLambda_T(-\omega_{14}^3, -\omega_{\boldsymbol{k}2}^{1}) \right]\nonumber\\ & \quad + 2 \sum_{1,2,3,4} V_{12}^{\boldsymbol{k}} \delta_{\boldsymbol{k}2}^1 \left[ V_{34}^2 \delta_{34}^2 c_1^{(0)} c_3^{(0)*} c_4^{(0)*} \varLambda_T(-\omega_{34}^2, -\omega_{\boldsymbol{k}2}^{1}) \right.\nonumber\\&\left. \quad +\, 2 V_{34}^2 \delta_{24}^3 c_1^{(0)} c_3^{(0)*} c_4^{(0)} \varLambda_T(\omega_{24}^3, -\omega_{\boldsymbol{k}2}^{1}) \right], \end{align}
\begin{align} c_{\boldsymbol{k}}^{(2)}(T) &={-} 2 \sum_{1,2,3,4} V_{12}^{\boldsymbol{k}} \delta_{12}^{\boldsymbol{k}} \left[V_{34}^2 \delta_{34}^2 c_1^{(0)} c_3^{(0)} c_4^{(0)} \varLambda_T(\omega_{34}^2, \omega_{12}^{\boldsymbol{k}}) \right.\nonumber\\ &\left.\quad +\, 2 V_{34}^2 \delta_{24}^3 c_1^{(0)} c_3^{(0)} c_4^{(0)*} \varLambda_T(-\omega_{24}^3, \omega_{12}^{\boldsymbol{k}}) \right]\nonumber\\ & \quad - 2 \sum_{1,2,3,4} V_{12}^{\boldsymbol{k}} \delta_{\boldsymbol{k}2}^1 \left[ V_{34}^1 \delta_{34}^1 c_2^{(0)*} c_3^{(0)} c_4^{(0)} \varLambda_T(\omega_{34}^1, -\omega_{\boldsymbol{k}2}^{1}) \right.\nonumber\\ &\left. \quad +\, 2 V_{34}^1 \delta_{14}^3 c_2^{(0)*} c_3^{(0)} c_4^{(0)*} \varLambda_T(-\omega_{14}^3, -\omega_{\boldsymbol{k}2}^{1}) \right]\nonumber\\ & \quad + 2 \sum_{1,2,3,4} V_{12}^{\boldsymbol{k}} \delta_{\boldsymbol{k}2}^1 \left[ V_{34}^2 \delta_{34}^2 c_1^{(0)} c_3^{(0)*} c_4^{(0)*} \varLambda_T(-\omega_{34}^2, -\omega_{\boldsymbol{k}2}^{1}) \right.\nonumber\\&\left. \quad +\, 2 V_{34}^2 \delta_{24}^3 c_1^{(0)} c_3^{(0)*} c_4^{(0)} \varLambda_T(\omega_{24}^3, -\omega_{\boldsymbol{k}2}^{1}) \right], \end{align}
where ![]() $\varGamma _T(x) \equiv \int _{0}^{T} {\rm e}^{ixt} \,\mathrm {d} t$ and
$\varGamma _T(x) \equiv \int _{0}^{T} {\rm e}^{ixt} \,\mathrm {d} t$ and ![]() $\varLambda _T(x,y) \equiv \int _{0}^{T} \varGamma _T(x) {\rm e}^{iyt} \,\mathrm {d} t$. We need to compute
$\varLambda _T(x,y) \equiv \int _{0}^{T} \varGamma _T(x) {\rm e}^{iyt} \,\mathrm {d} t$. We need to compute
at time ![]() $T$, where
$T$, where ![]() $\langle \cdot \rangle$ denotes an ensemble average over possible initial conditions. To this end, we need a closure hypothesis to compute the correlations. In WWT, we use the random phase and amplitude (RPA) hypothesis, which considers that waves have initially random and independent amplitudes and phases, with the phases uniformly distributed in
$\langle \cdot \rangle$ denotes an ensemble average over possible initial conditions. To this end, we need a closure hypothesis to compute the correlations. In WWT, we use the random phase and amplitude (RPA) hypothesis, which considers that waves have initially random and independent amplitudes and phases, with the phases uniformly distributed in ![]() $[0, 2 {\rm \pi}[$. Within this approximation, we have (Nazarenko Reference Nazarenko2011)
$[0, 2 {\rm \pi}[$. Within this approximation, we have (Nazarenko Reference Nazarenko2011)
 \begin{align} \left. \begin{aligned} \left\langle c_1 c_2 \right\rangle & = 0, \quad \left\langle c_1 c_2^* \right\rangle = \left\langle |c_1^{(0)}|^2 \right\rangle \delta_{12},\\ \left\langle c_1 c_2 c_3 \right\rangle & = \left\langle c_1 c_2 c_3^* \right\rangle = 0, \quad \left\langle c_1 c_2 c_3 c_4 \right\rangle = \left\langle c_1 c_2 c_3 c_4^* \right\rangle = 0,\\ \left\langle c_1 c_2 c_3^* c_4^* \right\rangle & = \delta_{13} \delta_{24} \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_2^{(0)}|^2 \right\rangle + \delta_{14} \delta_{23} \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_2^{(0)}|^2 \right\rangle - \delta_{12} \delta_{13} \delta_{14} \left\langle |c_1^{(0)} |^4\right\rangle. \end{aligned} \right\} \end{align}
\begin{align} \left. \begin{aligned} \left\langle c_1 c_2 \right\rangle & = 0, \quad \left\langle c_1 c_2^* \right\rangle = \left\langle |c_1^{(0)}|^2 \right\rangle \delta_{12},\\ \left\langle c_1 c_2 c_3 \right\rangle & = \left\langle c_1 c_2 c_3^* \right\rangle = 0, \quad \left\langle c_1 c_2 c_3 c_4 \right\rangle = \left\langle c_1 c_2 c_3 c_4^* \right\rangle = 0,\\ \left\langle c_1 c_2 c_3^* c_4^* \right\rangle & = \delta_{13} \delta_{24} \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_2^{(0)}|^2 \right\rangle + \delta_{14} \delta_{23} \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_2^{(0)}|^2 \right\rangle - \delta_{12} \delta_{13} \delta_{14} \left\langle |c_1^{(0)} |^4\right\rangle. \end{aligned} \right\} \end{align}It is then possible to compute all the terms in (A4) using ((A1)–(A3)) and the previous expressions (A5). The second term on the right-hand side in (A4) is
because the triple correlations vanish under the RPA hypothesis. The third term is
 \begin{align} \left\langle \left| c_{\boldsymbol{k}}^{(1)} \right|^2 \right\rangle &= 2 \sum_{1,2} |V_{12}^{\boldsymbol{k}}|^2 \delta_{12}^{\boldsymbol{k}} |\varGamma_T(\omega_{12}^{\boldsymbol{k}})|^2 \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_2^{(0)}|^2 \right\rangle\nonumber\\ &\quad + 4 \sum_{1,2} |V_{12}^{\boldsymbol{k}}|^2 \delta_{\boldsymbol{k}2}^1 |\varGamma_T(\omega_{\boldsymbol{k}2}^{1})|^2 \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_2^{(0)}|^2 \right\rangle\nonumber\\ &\quad + \sum_{1} |V_{11}^{\boldsymbol{k}}|^2 \delta_{11}^{\boldsymbol{k}} |\varGamma_T(\omega_{11}^{\boldsymbol{k}})|^2 \left\langle |c_1^{(0)}|^4 \right\rangle\nonumber\\ &\quad + 4 \sum_{1,3} V_{11}^{\boldsymbol{k}} V_{33}^{\boldsymbol{k}} \delta_{\boldsymbol{k}1}^1 \delta_{\boldsymbol{k}3}^3 \varGamma_T^*(\omega_{\boldsymbol{k}1}^{1}) \varGamma_T(\omega_{\boldsymbol{k}3}^{3}) \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_3^{(0)}|^2 \right\rangle\nonumber\\ &\quad + 4 \sum_{1} |V_{11}^{\boldsymbol{k}}|^2 \delta_{\boldsymbol{k}1}^{1} |\varGamma_T(\omega_{\boldsymbol{k}1}^{1})|^2 \left\langle |c_1^{(0)}|^4 \right\rangle. \end{align}
\begin{align} \left\langle \left| c_{\boldsymbol{k}}^{(1)} \right|^2 \right\rangle &= 2 \sum_{1,2} |V_{12}^{\boldsymbol{k}}|^2 \delta_{12}^{\boldsymbol{k}} |\varGamma_T(\omega_{12}^{\boldsymbol{k}})|^2 \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_2^{(0)}|^2 \right\rangle\nonumber\\ &\quad + 4 \sum_{1,2} |V_{12}^{\boldsymbol{k}}|^2 \delta_{\boldsymbol{k}2}^1 |\varGamma_T(\omega_{\boldsymbol{k}2}^{1})|^2 \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_2^{(0)}|^2 \right\rangle\nonumber\\ &\quad + \sum_{1} |V_{11}^{\boldsymbol{k}}|^2 \delta_{11}^{\boldsymbol{k}} |\varGamma_T(\omega_{11}^{\boldsymbol{k}})|^2 \left\langle |c_1^{(0)}|^4 \right\rangle\nonumber\\ &\quad + 4 \sum_{1,3} V_{11}^{\boldsymbol{k}} V_{33}^{\boldsymbol{k}} \delta_{\boldsymbol{k}1}^1 \delta_{\boldsymbol{k}3}^3 \varGamma_T^*(\omega_{\boldsymbol{k}1}^{1}) \varGamma_T(\omega_{\boldsymbol{k}3}^{3}) \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_3^{(0)}|^2 \right\rangle\nonumber\\ &\quad + 4 \sum_{1} |V_{11}^{\boldsymbol{k}}|^2 \delta_{\boldsymbol{k}1}^{1} |\varGamma_T(\omega_{\boldsymbol{k}1}^{1})|^2 \left\langle |c_1^{(0)}|^4 \right\rangle. \end{align}
At this point, we see that the last 3 lines will lead to interactions with shear modes. Generally speaking, all terms where the same index is repeated more than two times in a ![]() $\delta$ (e.g.
$\delta$ (e.g. ![]() $\delta _{11}^{\boldsymbol {k}}$,
$\delta _{11}^{\boldsymbol {k}}$, ![]() $\delta _{1\boldsymbol {k}}^{1}$,…) correspond to interactions with shear modes in the limit
$\delta _{1\boldsymbol {k}}^{1}$,…) correspond to interactions with shear modes in the limit ![]() $\epsilon \rightarrow 0$. To obtain the wave-kinetic equation, it is therefore sufficient to consider only the two first terms of the above equation in the following computations. The last term to compute in (A4) is
$\epsilon \rightarrow 0$. To obtain the wave-kinetic equation, it is therefore sufficient to consider only the two first terms of the above equation in the following computations. The last term to compute in (A4) is
 \begin{align} \left\langle c_{\boldsymbol{k}}^{(0)*} c_{\boldsymbol{k}}^{(2)} + {\rm c.c.} \right\rangle &={-} 8 \sum_{1,2} \delta_{12}^{\boldsymbol{k}} V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}1}^{2} \mathrm{Re} \left[ \varLambda_T(-\omega_{21}^{\boldsymbol{k}}, \omega_{12}^{\boldsymbol{k}}) \right] \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_{\boldsymbol{k}}^{(0)}|^2 \right\rangle\nonumber\\ &\quad - 8 \sum_{1,2} \delta_{\boldsymbol{k}2}^1 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}2}^{1} \mathrm{Re} \left[ \varLambda_T(\omega_{\boldsymbol{k}2}^{1}, -\omega_{\boldsymbol{k}2}^{1}) \right] \left\langle |c_2^{(0)}|^2 \right\rangle \left\langle |c_{\boldsymbol{k}}^{(0)}|^2 \right\rangle\nonumber\\ &\quad + 8 \sum_{1,2} \delta_{\boldsymbol{k}2}^1 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}1}^{2} \mathrm{Re} \left[ \varLambda_T(\omega_{\boldsymbol{k}2}^{1}, -\omega_{\boldsymbol{k}2}^{1}) \right] \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_{\boldsymbol{k}}^{(0)}|^2 \right\rangle, \end{align}
\begin{align} \left\langle c_{\boldsymbol{k}}^{(0)*} c_{\boldsymbol{k}}^{(2)} + {\rm c.c.} \right\rangle &={-} 8 \sum_{1,2} \delta_{12}^{\boldsymbol{k}} V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}1}^{2} \mathrm{Re} \left[ \varLambda_T(-\omega_{21}^{\boldsymbol{k}}, \omega_{12}^{\boldsymbol{k}}) \right] \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_{\boldsymbol{k}}^{(0)}|^2 \right\rangle\nonumber\\ &\quad - 8 \sum_{1,2} \delta_{\boldsymbol{k}2}^1 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}2}^{1} \mathrm{Re} \left[ \varLambda_T(\omega_{\boldsymbol{k}2}^{1}, -\omega_{\boldsymbol{k}2}^{1}) \right] \left\langle |c_2^{(0)}|^2 \right\rangle \left\langle |c_{\boldsymbol{k}}^{(0)}|^2 \right\rangle\nonumber\\ &\quad + 8 \sum_{1,2} \delta_{\boldsymbol{k}2}^1 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}1}^{2} \mathrm{Re} \left[ \varLambda_T(\omega_{\boldsymbol{k}2}^{1}, -\omega_{\boldsymbol{k}2}^{1}) \right] \left\langle |c_1^{(0)}|^2 \right\rangle \left\langle |c_{\boldsymbol{k}}^{(0)}|^2 \right\rangle, \end{align}where we have omitted interactions with the shear modes. The wave-action spectrum (3.3), therefore, satisfies the equation
The next step is to take the infinite size limit ![]() $L \rightarrow \infty$, which is achieved by replacing
$L \rightarrow \infty$, which is achieved by replacing ![]() $\sum _{1,2} \rightarrow ({L}/{2 {\rm \pi}})^{6} \int \,\mathrm {d}^3\boldsymbol {k}_1 \,\mathrm {d}^3\boldsymbol {k}_2$ and
$\sum _{1,2} \rightarrow ({L}/{2 {\rm \pi}})^{6} \int \,\mathrm {d}^3\boldsymbol {k}_1 \,\mathrm {d}^3\boldsymbol {k}_2$ and ![]() $\delta _{12}^{\boldsymbol {k}} \rightarrow ({2 {\rm \pi}}/{L})^3 \delta (\boldsymbol {k} - \boldsymbol {k}_1 - \boldsymbol {k}_2 )$ in (A9). Secondly, we take
$\delta _{12}^{\boldsymbol {k}} \rightarrow ({2 {\rm \pi}}/{L})^3 \delta (\boldsymbol {k} - \boldsymbol {k}_1 - \boldsymbol {k}_2 )$ in (A9). Secondly, we take ![]() $\epsilon \rightarrow 0$ such that
$\epsilon \rightarrow 0$ such that ![]() $\lim _{T \rightarrow \infty } | \varGamma _T(\omega ) |^2 = 2 {\rm \pi}T \delta (\omega )$ and
$\lim _{T \rightarrow \infty } | \varGamma _T(\omega ) |^2 = 2 {\rm \pi}T \delta (\omega )$ and ![]() $\lim _{T \rightarrow \infty } \mathrm {Re} [ \varLambda _T(-\omega,\omega ) ] = {\rm \pi}T \delta (\omega )$. In the end, we obtain
$\lim _{T \rightarrow \infty } \mathrm {Re} [ \varLambda _T(-\omega,\omega ) ] = {\rm \pi}T \delta (\omega )$. In the end, we obtain
 \begin{align}\frac{n_{\boldsymbol{k}}(T) - n_{\boldsymbol{k}}(0)}{T} &= 4 {\rm \pi}\epsilon^2 \int \,\mathrm{d}^3\boldsymbol{k}_1\,\mathrm{d}^3\boldsymbol{k}_2 \nonumber\\ &\quad \times \left\{|V_{12}^{\boldsymbol{k}}|^2 \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2 ) \delta(\omega_{\boldsymbol{k}} - \omega_{1} - \omega_{2} ) n_1(0) n_2(0) \right. \nonumber\\ &\quad + 2 |V_{12}^{\boldsymbol{k}}|^2 \delta(\boldsymbol{k}_1 - \boldsymbol{k} - \boldsymbol{k}_2 ) \delta(\omega_{1} - \omega_{\boldsymbol{k}} - \omega_{2} ) n_1(0) n_2(0) \nonumber\\ &\quad - 2 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}1}^{2} \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2 ) \delta(\omega_{\boldsymbol{k}} - \omega_{1} - \omega_{2} ) n_1(0) n_{\boldsymbol{k}}(0) \nonumber\\ &\quad- 2 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}2}^{1} \delta(\boldsymbol{k}_1 - \boldsymbol{k} - \boldsymbol{k}_2 ) \delta(\omega_{1} - \omega_{\boldsymbol{k}} - \omega_{2} ) n_2(0) n_{\boldsymbol{k}}(0) \nonumber\\ &\quad \left. +\, 2 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}1}^{2} \delta(\boldsymbol{k}_1 - \boldsymbol{k} - \boldsymbol{k}_2 ) \delta(\omega_{1} - \omega_{\boldsymbol{k}} - \omega_{2} ) n_1(0) n_{\boldsymbol{k}}(0) \right\} + O(\epsilon^3). \end{align}
\begin{align}\frac{n_{\boldsymbol{k}}(T) - n_{\boldsymbol{k}}(0)}{T} &= 4 {\rm \pi}\epsilon^2 \int \,\mathrm{d}^3\boldsymbol{k}_1\,\mathrm{d}^3\boldsymbol{k}_2 \nonumber\\ &\quad \times \left\{|V_{12}^{\boldsymbol{k}}|^2 \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2 ) \delta(\omega_{\boldsymbol{k}} - \omega_{1} - \omega_{2} ) n_1(0) n_2(0) \right. \nonumber\\ &\quad + 2 |V_{12}^{\boldsymbol{k}}|^2 \delta(\boldsymbol{k}_1 - \boldsymbol{k} - \boldsymbol{k}_2 ) \delta(\omega_{1} - \omega_{\boldsymbol{k}} - \omega_{2} ) n_1(0) n_2(0) \nonumber\\ &\quad - 2 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}1}^{2} \delta(\boldsymbol{k} - \boldsymbol{k}_1 - \boldsymbol{k}_2 ) \delta(\omega_{\boldsymbol{k}} - \omega_{1} - \omega_{2} ) n_1(0) n_{\boldsymbol{k}}(0) \nonumber\\ &\quad- 2 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}2}^{1} \delta(\boldsymbol{k}_1 - \boldsymbol{k} - \boldsymbol{k}_2 ) \delta(\omega_{1} - \omega_{\boldsymbol{k}} - \omega_{2} ) n_2(0) n_{\boldsymbol{k}}(0) \nonumber\\ &\quad \left. +\, 2 V_{12}^{\boldsymbol{k}} V_{\boldsymbol{k}1}^{2} \delta(\boldsymbol{k}_1 - \boldsymbol{k} - \boldsymbol{k}_2 ) \delta(\omega_{1} - \omega_{\boldsymbol{k}} - \omega_{2} ) n_1(0) n_{\boldsymbol{k}}(0) \right\} + O(\epsilon^3). \end{align}Using the approximation ![]() $({n_{\boldsymbol {k}}(T) - n_{\boldsymbol {k}}(0)})/{T} \simeq \dot {n}_{\boldsymbol {k}}$ and rearranging the terms allow us to obtain the kinetic equation for weakly nonlinear IGWs ((3.4)–(3.6)).
$({n_{\boldsymbol {k}}(T) - n_{\boldsymbol {k}}(0)})/{T} \simeq \dot {n}_{\boldsymbol {k}}$ and rearranging the terms allow us to obtain the kinetic equation for weakly nonlinear IGWs ((3.4)–(3.6)).




































