Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T10:50:07.081Z Has data issue: false hasContentIssue false
  • English
  • Français

On the internal flow of a ventilated supercavity

Published online by Cambridge University Press:  16 January 2019

Yue Wu ,
Yun Liu ,
Siyao Shao  and
Jiarong Hong Open the ORCID record for Jiarong Hong [Opens in a new window]
Yue Wu
Affiliation:
St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA
Yun Liu
Affiliation:
St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Mechanical and Civil Engineering, Purdue University Northwest, Westville, IN 46391, USA
Siyao Shao
Affiliation:
St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Jiarong Hong*
Affiliation:
St. Anthony Falls Laboratory, University of Minnesota, Minneapolis, MN 55414, USA Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study presents an experimental investigation on the internal flow of a ventilated supercavity using fog flow visualization and particle image velocimetry (PIV) measurements. The ventilated supercavity is generated on a backward-facing cavitator and studied in the high-speed water tunnel at St. Anthony Falls Laboratory. Fog particles are introduced into the supercavity through the ventilation line, and then illuminated by a laser sheet for flow visualizations and PIV measurements. The experiments are performed on the supercavities with two closure types, i.e. the re-entrant jet (RJ) and the twin vortex (TV), under the same water tunnel flow condition but different ventilation rates. The flow visualization revealed three distinct regions within the supercavity, including the ventilation influence region near the cavitator, the extended internal boundary layer along the liquid–gas interface and the reverse flow region occupying a large centre portion of the supercavity. The streamwise and vertical extent of the ventilation influence region, the streamwise growth of the internal boundary layer and the reverse flow within the supercavity are then quantified through PIV flow measurements. Compared to the RJ case, the results indicate that the TV supercavity yields a longer vertical extent of the ventilation influence region, a thinner internal boundary layer and a stronger reverse flow. The internal flow results suggest that at the upstream of the location of the maximum cavity diameter, the gas enters the forward flow (including the internal boundary layer and the forward moving portion of the ventilation influence region) from the reverse flow, while at the downstream of that location, the gas is stripped from the internal boundary layer and enters the reverse flow due to the increasing adverse pressure gradient in the streamwise direction. The above results are combined with visualization results of the supercavity geometry and closure patterns to further explain the influence of gas leakage mechanisms on cavity growth and closure transition. Specifically, visualization of the cavity geometry change during the RJ to TV supercavity transition indicates external flow separation associated with a critical incline angle of the bottom liquid–gas interface at the closure contributes to the onset of RJ closure. The closure visualization shows the coexistence of the toroidal vortex and twin-vortex tubes for the RJ supercavity leads to two gas leakage mechanisms: one associated with the shedding of toroidal vortices (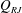$Q_{RJ}$) and the other due to the gas entrained by the internal boundary layer and leaking from the twin-vortex tubes (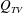$Q_{TV}$). For the RJ supercavity, with increasing ventilation input, due to the reduction of 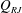$Q_{RJ}$, the supercavity needs to elongate to increase the gas entrained by the internal boundary layer (i.e. 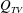$Q_{TV}$) to balance the ventilation increase. The elongation of the supercavity leads to reduced flow separation, and eventually a transition to the TV supercavity with ventilation above a critical value. For the TV supercavity, 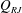$Q_{RJ}$ is absent. An increase of ventilation input can be balanced by the increase of 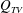$Q_{TV}$ associated with the widening of the twin-vortex tubes, and therefore, no appreciable elongation of cavity length is observed.

JFM classification

Drops and Bubbles: Cavitation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 1135 - 1165
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, P. S., Kays, W. M. & Moffat, R. J.1972 The turbulent boundary layer on a porous plate: an experimental study of the fluid mechanics for adverse free stream pressure gradients. NASA report.Google Scholar
Cao, L., Karn, A., Arndt, R., Wang, Z. & Hong, J. 2017 Numerical investigation of pressure distribution inside ventilated supercavity. J. Fluids Engng 139 (2), 021301.Google Scholar
Cebeci, T. & Bradshaw, P. 2012 Physical and Computational Aspects of Convective Heat Transfer. Springer Science & Business Media.Google Scholar
Cox, R. & Clayden, W. 1955 Air entrainment at the rear of a steady cavity. In Proceedings of the Symposium on Cavitation in Hydrodynamics. HMSO.Google Scholar
Epshtein, L. 1973 Characteristics of ventilated cavities and some scale effects. In Proceedings of the International Symposium IUTAM, Unsteady Water Flow with High Velocities, pp. 173–185. Nauka.Google Scholar
Gadd, G. & Grant, S. 1965 Some experiments on cavities behind disks. J. Fluid Mech. 23 (4), 645–656.10.1017/S002211206500160XGoogle Scholar
Ishak, A., Nazar, R. & Pop, I. 2007 Falkner–Skan equation for flow past a moving wedge with suction or injection. J. Appl. Maths Comput. 25 (1–2), 67–83.10.1007/BF02832339Google Scholar
Jackson, P. S. & Hunt, J. C. R. 1975 Turbulent wind flow over a low hill. Q. J. R. Meteorol. Soc. 101 (430), 929–955.10.1002/qj.49710143015Google Scholar
Karn, A., Arndt, R. E. A. & Hong, J. 2015 Dependence of supercavity closure upon flow unsteadiness. Exp. Therm. Fluid Sci. 68, 493–498.10.1016/j.expthermflusci.2015.06.011Google Scholar
Karn, A., Arndt, R. E. A. & Hong, J. 2016a An experimental investigation into supercavity closure mechanisms. J. Fluid Mech. 789, 259–284.10.1017/jfm.2015.680Google Scholar
Karn, A., Arndt, R. E. A. & Hong, J. 2016b Bubble coalescence and breakup in turbulent bubbly wake of a ventilated hydrofoil. Exp. Therm. Fluid Sci. 70, 397–407.10.1016/j.expthermflusci.2015.10.003Google Scholar
Karn, A., Arndt, R. E. A. & Hong, J. 2016c Gas entrainment behaviors in the formation and collapse of a ventilated supercavity. Exp. Therm. Fluid Sci. 79, 294–300.10.1016/j.expthermflusci.2016.08.003Google Scholar
Kawakami, E. & Arndt, R. E. A. 2011 Investigation of the behavior of ventilated supercavities. J. Fluid Engng 133 (9), 091305.Google Scholar
Kinzel, M. P., Krane, M. H., Kirschner, I. N. & Moeny, M. J. 2017 A numerical assessment of the interaction of a supercavitating flow with a gas jet. Ocean Engng 136, 304–313.10.1016/j.oceaneng.2017.03.042Google Scholar
Kinzel, M. P., Lindau, J. W. & Kunz, R. F. 2009 Air entrainment mechanisms from artificial supercavities: insight based on numerical simulations. In Proceedings of the 7th International Symposium on Cavitation, CAV 2009, Ann Arbor, vol. 136. University of Michigan.Google Scholar
Kirschner, I. N., Fine, N. E., Uhlman, J. S. & Kring, D. C.2001 Numerical modeling of supercavitating flows. Tech. Rep. Anteon/Engineering Technology Center.Google Scholar
Kubota, A., Kato, H. & Yamaguchi, H. 1992 A new modelling of cavitating flows: a numerical study of unsteady cavitation on a hydrofoil section. J. Fluid Mech. 240, 59–96.10.1017/S002211209200003XGoogle Scholar
Kumar, S. S. & Hong, J. 2018 Digital Fresnel reflection holography for high-resolution 3D near-wall flow measurement. Opt. Express 26 (10), 12779–12789.10.1364/OE.26.012779Google Scholar
Kumar, S. S., Karn, A., Arndt, R. E. & Hong, J. 2017 Internal flow measurements of drop impacting a solid surface. Exp. Fluids 58 (3), 12.10.1007/s00348-016-2293-7Google Scholar
Liu, X. & Katz, J. 2013 Vortex-corner interactions in a cavity shear layer elucidated by time-resolved measurements of the pressure field. J. Fluid Mech. 728, 417–457.10.1017/jfm.2013.275Google Scholar
Logvinovich, G. V. 1972 Hydrodynamics of Free-boundary Flows. Halsted Press.Google Scholar
Moore, F. K. 1958 On the separation of the unsteady laminar boundary layer. In Grenzschichtforschung/Boundary Layer Research, pp. 296–311. Springer.10.1007/978-3-642-45885-9_23Google Scholar
Nesteruk, I. 2012 Supercavitation: Advances and Perspectives. A Collection Dedicated to the 70th Jubilee of Yu. N. Savchenko. Springer Science and Business Media.10.1007/978-3-642-23656-3Google Scholar
Raffel, M., Willert, C. E. & Kompenhans, J. 2007 Particle Image Velocimetry: A Practical Guide. Springer Science and Business Media.10.1007/978-3-540-72308-0Google Scholar
Rhie, C. M. & Chow, W. L. 1983 Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 21 (11), 1525–1532.10.2514/3.8284Google Scholar
Riley, N. & Weidman, P. D. 1989 Multiple solutions of the Falkner–Skan equation for flow past a stretching boundary. J. Appl. Maths 49 (5), 1350–1358.Google Scholar
Roth, G. I. & Katz, J. 2001 Five techniques for increasing the speed and accuracy of PIV interrogation. Meas. Sci. Technol. 12 (3), 238–245.10.1088/0957-0233/12/3/302Google Scholar
Rott, N. 1956 Unsteady viscous flow in the vicinity of a stagnation point. Q. Appl. Maths 13 (4), 444–451.10.1090/qam/74194Google Scholar
Savchenko, Y. N. & Savchenko, G. Y. 2012 Gas flows in ventilated supercavities. In Supercavitation, pp. 115–126. Springer.10.1007/978-3-642-23656-3_7Google Scholar
Schlichting, H., Gersten, K., Krause, E. & Qertel, H. 1955 Boundary-layer Theory. vol. 7. McGraw-Hill.Google Scholar
Sears, W. R. & Telionis, D. P. 1975 Boundary-layer separation in unsteady flow. J. Appl. Maths 28 (1), 215–235.Google Scholar
Semenenko, V. N. 2001 Artificial Supercavitation: Physics and Calculation. Ukrainian Academy of Sciences, Kiev Institute of Hydromechanics.Google Scholar
Shao, S., Karn, A., Ahn, B. K., Arndt, R. E. A. & Hong, J. 2017 A comparative study of natural and ventilated supercavitation across two closed-wall water tunnel facilities. Exp. Therm. Fluid Sci. 88, 519–529.10.1016/j.expthermflusci.2017.07.005Google Scholar
Shao, S., Wu, Y., Haynes, J., Arndt, R. E. & Hong, J. 2018 Investigation into the behaviors of ventilated supercavities in unsteady flow. Phys. Fluids 30 (5), 052102.10.1063/1.5027629Google Scholar
Simons, M. & Simons, M. 1999 Model Aircraft Aerodynamics. Nexus Special Interests.Google Scholar
Spurk, J. 2002 On the gas loss from ventilated supercavities. Acta Mechanica 155, 125–135.10.1007/BF01176238Google Scholar
Stewartson, K. 1954 Further solutions of the Falkner–Skan equation. Math. Proc. Camb. Phil. Soc. 50 (3), 454–465.10.1017/S030500410002956XGoogle Scholar
Toloui, M., Mallery, K. & Hong, J. 2017 Improvements on digital inline holographic PTV for 3D wall-bounded turbulent flow measurements. Meas. Sci. Technol. 28 (4), 044009.10.1088/1361-6501/aa5c4dGoogle Scholar
Wang, Z., Huang, B., Zhang, M., Wang, G. & Zhao, X. A. 2018 Experimental and numerical investigation of ventilated cavitating flow structures with special emphasis on vortex shedding dynamics. Intl J. Multiphase Flow 98, 79–95.10.1016/j.ijmultiphaseflow.2017.08.014Google Scholar
Wu, T. 1972 Cavity and wake flows. Annu. Rev. Fluid Mech. 4, 243–284.10.1146/annurev.fl.04.010172.001331Google Scholar
Zhou, J., Yu, K., Min, J. & Yang, M. 2010 The comparative study of ventilated super cavity shape in water tunnel and infinite flow field. J. Hydrodyn. B 22 (5), 689–696.Google Scholar

Wu et al. supplementary movie 1

Supplemental movie showing the far view visualization of the internal flow of RJ supercavity using fog particles.

Download Wu et al. supplementary movie 1(Video)
Video 7 MB

Wu et al. supplementary movie 2

Supplemental movie showing the close view visualization of the internal flow near the cavitator of RJ supercavity using fog particles.

Download Wu et al. supplementary movie 2(Video)
Video 15.1 MB

Wu et al. supplementary movie 3

Supplemental movie showing the far view visualization of the internal flow of TV supercavity using fog particles.

Download Wu et al. supplementary movie 3(Video)
Video 8.5 MB

Wu et al. supplementary movie 4

Supplemental movie showing the close view visualization of the internal flow near the cavitator of TV supercavity using fog particles.

Download Wu et al. supplementary movie 4(Video)
Video 24.4 MB

Wu et al. supplementary movie 5

Supplemental movie showing the tracers in the water move towards the interface at the closure region.

Download Wu et al. supplementary movie 5(Video)
Video 17.3 MB