Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T09:17:51.883Z Has data issue: false hasContentIssue false
  • English
  • Français

On the interaction of a planar shock with a light polygonal interface

Published online by Cambridge University Press:  26 September 2014

Zhigang Zhai ,
Minghu Wang ,
Ting Si  and
Xisheng Luo
Zhigang Zhai
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Minghu Wang
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Ting Si
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Xisheng Luo*
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China State Key Laboratory of Fire Science, University of Science and Technology of China, Hefei 230026, China
*
†Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The interaction of a planar shock wave with a polygonal 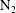$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathrm{N}}_2$ volume surrounded by 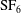${\mathrm{SF}}_6$ is investigated experimentally and numerically. Three polygonal interfaces (square, triangle and diamond) are formed by the soap film technique developed in our previous work, in which thin pins are introduced as angular vertexes to connect adjacent sides of polygonal soap films. The evolutions of the shock-accelerated polygonal interfaces are then visualized by a high-speed schlieren system. Wave systems and interface structures can be clearly identified in experimental schlieren images, and agree well with the numerical ones. Quantitatively, the movement of the distorted interface, and the length and height of the interface structures are further compared and good agreements are achieved between experimental and numerical results. It is found that the evolution of these polygonal interfaces is closely related to their initial shapes. In the square interface, two vortices are generated shortly after the shock impact around the left corner and dominate the flow field at late stages. In the triangular and diamond cases, the most remarkable feature is the small ‘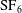${\mathrm{SF}}_6$ jet’ which grows constantly with time and penetrates the downstream boundary of the interface, forming two independent vortices. These distinct morphologies of the three polygonal interfaces also lead to the different behaviours of the interface features including the length and height. It is also found that the velocities of the vortex pair predicted from the theory of Rudinger and Somers (J. Fluid Mech., vol. 7, 1960, pp. 161–176) agree with the experimental ones, especially for the square case. Typical free precursor irregular refraction phenomena and the transitions among them are observed and analysed, which gives direct experimental evidence for wave patterns and their transitions at a slow/fast interface. The velocities of triple points and shocks are experimentally measured. It is found that the transmitted shock near the interface boundary has weakened into an evanescent wave.

JFM classification

Compressible Flows: Compressible Flows Mixing: Mixing Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 800 - 816
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© 2014 Cambridge University Press

References

Abd-el Fattah, A. M. & Henderson, L. F. 1978a Shock waves at a fast–slow gas interface. J. Fluid Mech. 86, 15–32.Google Scholar
Abd-el Fattah, A. M. & Henderson, L. F. 1978b Shock waves at a slow–fast gas interface. J. Fluid Mech. 89, 79–95.CrossRefGoogle Scholar
Abd-el Fattah, A. M., Henderson, L. F. & Lozzi, A. 1976 Precursor shock waves at a slow–fast gas interface. J. Fluid Mech. 76, 157–176.CrossRefGoogle Scholar
Arnett, W. D., Bahcall, J. N., Kirshner, R. P. & Woosley, S. E. 1989 Supernova 1987A. Annu. Rev. Astron. Astrophys. 27, 629–700.Google Scholar
Balakumar, B. J., Orlicz, G. C., Ristorcelli, J. R., Balasubramanian, S., Prestridge, K. P. & Tomkins, C. D. 2012 Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics. J. Fluid Mech. 696, 67–93.CrossRefGoogle Scholar
Balasubramanian, S., Orlicz, G. C., Prestridge, K. P. & Balakumar, B. J. 2012 Experimental study of initial condition dependence on Richtmyer–Meshkov instability in the presence of reshock. Phys. Fluids 24, 034103.CrossRefGoogle Scholar
Bates, K. R., Nikiforakis, N. & Holder, D. 2007 Richtmyer–Meshkov instability induced by the interaction of a shock wave with a rectangular block of ${\mathrm{SF}}_6$ . Phys. Fluids 19, 036101.CrossRefGoogle Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.CrossRefGoogle Scholar
Haas, J. F. & Sturtevant, B. 1987 Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities. J. Fluid Mech. 181, 41–76.CrossRefGoogle Scholar
Haehn, N., Ranjan, D., Weber, C., Oakley, J., Rothamer, D. & Bonazza, R. 2012 Reacting shock bubble interaction. Combust. Flame 159, 1339–1350.CrossRefGoogle Scholar
Haehn, N., Weber, C., Oakley, J. G., Anderson, M. H., Ranjan, D. & Bonazza, R. 2011 Experimental investigation of a twice-shocked spherical gas inhomogeneity with particle image velocimetry. Shock Waves 21, 225–231.CrossRefGoogle Scholar
Henderson, L. F. 1966 The refraction of a plane shock wave at a gas interface. J. Fluid Mech. 26, 607–637.Google Scholar
Henderson, L. F., Colella, P. & Puckett, E. G. 1991 On the refraction of shock waves at a slow–fast gas interface. J. Fluid Mech. 224, 1–27.CrossRefGoogle Scholar
Hosseini, S. H. R. & Takayama, K. 2005 Experimental study of Richtmyer–Meshkov instability induced by cylindrical shock waves. Phys. Fluids 17, 084101.CrossRefGoogle Scholar
Isenberg, C. 1992 The Science of Soap Films and Soap Bubbles. Dover.Google Scholar
Jacobs, J. W. 1992 Shock-induced mixing of a light-gas cylinder. J. Fluid Mech. 234, 629–649.CrossRefGoogle Scholar
Jacobs, J. W. 1993 The dynamics of shock accelerated light and heavy gas cylinders. Phys. Fluids A 5, 2239–2247.CrossRefGoogle Scholar
Jacobs, J. W., Klein, D. L., Jenkins, D. G. & Benjamin, R. F. 1993 Instability growth patterns of a shock-accelerated thin fluid layer. Phys. Rev. Lett. 70, 583–589.CrossRefGoogle ScholarPubMed
Jacobs, J. W. & Krivets, V. V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17, 034105.CrossRefGoogle Scholar
Jahn, R. G. 1956 The refraction of shock waves at a gaseous interface. J. Fluid Mech. 1, 457–489.CrossRefGoogle Scholar
Layes, G., Jourdan, G. & Houas, L. 2009 Experimental study on a plane shock wave accelerating a gas bubble. Phys. Fluids 21, 074102.CrossRefGoogle Scholar
Lindl, J. D., McCrory, R. L. & Campbell, E. M. 1992 Progress toward ignition and burn propagation in inertial confinement fusion. Phys. Today 45, 32–40.CrossRefGoogle Scholar
Long, C. C., Krivets, V. V., Greenough, J. A. & Jacobs, J. W. 2009 Shock tube experiments and numerical simulation of the single-mode, three-dimensional Richtmyer–Meshkov instability. Phys. Fluids 21, 114104.CrossRefGoogle Scholar
Luo, X., Wang, X. & Si, T. 2013 The Richtmyer–Meshkov instability of a three-dimensional air/ ${\mathrm{SF}}_6$ interface with a minimum-surface feature. J. Fluid Mech. 722, R2.CrossRefGoogle Scholar
Mariani, C., Vanderboomgaerde, M., Jourdan, G., Souffland, D. & Houas, L. 2008 Investigation of the Richtmyer–Meshkov instability with stereolithographed interfaces. Phys. Rev. Lett. 100, 254503.CrossRefGoogle ScholarPubMed
McFarland, J., Reilly, D., Creel, S., McDonald, C., Finn, T. & Ranjan, D. 2014 Experimental investigation of the inclined interface Richtmyer–Meshkov instability before and after reshock. Exp. Fluids 55, 1640–1653.CrossRefGoogle Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 101–104.CrossRefGoogle Scholar
Mikaelian, K. O. 2005 Richtmyer–Meshkov instability of arbitrary shapes. Phys. Fluids 17, 034101.CrossRefGoogle Scholar
Orlicz, G. C., Balakumar, B. J., Tomkins, C. D. & Prestridge, K. P. 2009 A Mach number study of the Richtmyer–Meshkov instability in a varicose, heavy-gas curtain. Phys. Fluids 21, 064102.CrossRefGoogle Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock–bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.CrossRefGoogle Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.CrossRefGoogle Scholar
Rudinger, G. & Somers, L. M. 1960 Behaviour of small regions of different gases carried in accelerated gas flows. J. Fluid Mech. 7, 161–176.CrossRefGoogle Scholar
Si, T., Zhai, Z., Luo, X. & Yang, J. 2012 Experimental studies of reshocked spherical gas interfaces. Phys. Fluids 24, 054101.CrossRefGoogle Scholar
Sun, M. & Takayama, K. 1999 Conservative smoothing on an adaptive quadrilateral grid. J. Comput. Phys. 150, 143–180.CrossRefGoogle Scholar
Tomkins, C. D., Balakumar, B. J., Orlicz, G. C., Prestridge, K. P. & Ristorcelli, J. R. 2013 Evolution of the density self-correlation in developing Richtmyer–Meshkov turbulence. J. Fluid Mech. 735, 288–306.CrossRefGoogle Scholar
Tomkins, C. D., Kumar, S., Orlicz, G. C. & Prestridge, K. P. 2008 An experimental investigation of mixing mechanisms in shock-accelerated flow. J. Fluid Mech. 611, 131–150.CrossRefGoogle Scholar
Wang, M., Si, T. & Luo, X. 2013 Generation of polygonal gas interfaces by soap film for Richtmyer–Meshkov instability study. Exp. Fluids 54, 1427–1435.CrossRefGoogle Scholar
Wang, T., Liu, J. H., Bai, J. S., Jiang, Y., Li, P. & Liu, K. 2012 Experimental and numerical investigation of inclined air/ ${\mathrm{SF}}_6$ interface instability under shock wave. Appl. Math. Mech. 33, 37–50.CrossRefGoogle Scholar
Zhai, Z., Si, T., Luo, X. & Yang, J. 2011 On the evolution of spherical gas interfaces accelerated by a planar shock wave. Phys. Fluids 23, 084104.CrossRefGoogle Scholar
Zhai, Z., Zhang, F., Si, T. & Luo, X. 2014 Evolution of heavy gas cylinder under reshock conditions. J. Vis. 17, 123–129.CrossRefGoogle Scholar
Zou, L. Y., Liu, C. L., Tan, D. W., Huang, W. B. & Luo, X. 2010 On interaction of shock wave with elliptic gas cylinder. J. Vis. 13, 347–353.CrossRefGoogle Scholar