Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T05:03:39.713Z Has data issue: false hasContentIssue false
  • English
  • Français

On the influence of collinear surface waves on turbulence in smooth-bed open-channel flows

Published online by Cambridge University Press:  04 August 2021

C. Peruzzi Open the ORCID record for C. Peruzzi [Opens in a new window] ,
D. Vettori Open the ORCID record for D. Vettori [Opens in a new window] ,
D. Poggi Open the ORCID record for D. Poggi [Opens in a new window] ,
P. Blondeaux Open the ORCID record for P. Blondeaux [Opens in a new window] ,
L. Ridolfi Open the ORCID record for L. Ridolfi [Opens in a new window]  and
C. Manes Open the ORCID record for C. Manes [Opens in a new window]
C. Peruzzi*
Affiliation:
Department of Environmental, Land and Infrastructure Engineering (DIATI), Politecnico di Torino, 10129Turin, Italy
D. Vettori
Affiliation:
Department of Environmental, Land and Infrastructure Engineering (DIATI), Politecnico di Torino, 10129Turin, Italy
D. Poggi
Affiliation:
Department of Environmental, Land and Infrastructure Engineering (DIATI), Politecnico di Torino, 10129Turin, Italy
P. Blondeaux
Affiliation:
Department of Civil, Chemical and Environmental Engineering (DICCA), University of Genoa, 16145Genoa, Italy
L. Ridolfi
Affiliation:
Department of Environmental, Land and Infrastructure Engineering (DIATI), Politecnico di Torino, 10129Turin, Italy
C. Manes
Affiliation:
Department of Environmental, Land and Infrastructure Engineering (DIATI), Politecnico di Torino, 10129Turin, Italy
*
Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

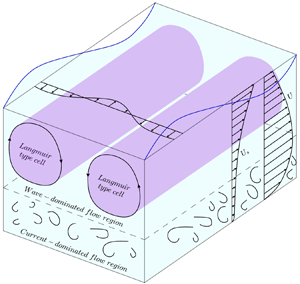
This work investigates how turbulence in open-channel flows is altered by the passage of surface waves by using experimental data collected with laboratory tests in a large-scale flume facility, wherein waves followed a current. Flow velocity data were measured with a laser Doppler anemometer and used to compute profiles of mean velocity and Reynolds stresses, and pre-multiplied spectra. The velocity signal containing contributions from the mean flow, wave motion and turbulence was decomposed using the empirical mode decomposition (EMD), which is considered a promising tool for the analysis of velocity time series measured in complex flows. A novel outer length scale $h_{0}$ is proposed which separates the flow into two regions depending on the competition between the vertical velocities associated with the wave motion and the turbulent velocities imposed by the current. This outer length scale allows for the identification of a genuine overlap layer and an insightful scaling of turbulent statistics in the current-dominated flow region (i.e. $y/h_{0} < 1$). As the wave contribution to the vertical velocity increases, the pre-multiplied spectra reveal two intriguing features: (i) in the current-dominated flow region, the very large-scale motions (VLSMs) are progressively weakened but attached eddies are still present; and (ii) in the wave-dominated flow region (i.e. $y/h_{0} > 1$), a new spectral signature associated with long turbulent structures (approximately 6 and 25 times the flow depth $h$) appears. These longitudinal structures present in the wave-dominated flow region seem to share many features with Langumir-type cells.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Turbulent Flows: Wave-turbulence interactions Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 924 , 10 October 2021 , A6
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: Department of Agricultural and Environmental Sciences (DiSAA), University of Milan, 20133 Milan, Italy.

References

REFERENCES

Baidya, R., Philip, J., Hutchins, N., Monty, J.P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.CrossRefGoogle Scholar
Banerjee, T., Muste, M. & Katul, G. 2015 Flume experiments on wind induced flow in static water bodies in the presence of protruding vegetation. Adv. Water Resour. 76, 11–28.CrossRefGoogle Scholar
Bell, J.H. & Mehta, R.D. 1988 Contraction design for small low-speed wind tunnels. NASA STI/Recon Tech. Rep. No. 89, 13753.Google Scholar
Bendat, J.S. & Piersol, A.G. 2011 Random Data: Analysis and Measurement Procedures, IV edn. John Wiley & Sons.Google Scholar
Benjamin, T.B. 1967 Instability of periodic wavetrains in nonlinear dispersive systems. Proc. R. Soc. Lond. A 299 (1456), 59–76.Google Scholar
Benjamin, T.B. & Feir, J.E. 1967 The disintegration of wave trains on deep water. Part 1. Theory. J. Fluid Mech. 27 (3), 417–430.CrossRefGoogle Scholar
Blondeaux, P. 1987 Turbulent boundary layer at the bottom of gravity waves. J. Hydraul. Res. 25 (4), 447–464.CrossRefGoogle Scholar
Blondeaux, P. 2001 Mechanics of coastal forms. Annu. Rev. Fluid Mech. 33 (1), 339–370.CrossRefGoogle Scholar
Cameron, S.M., Nikora, V.I. & Stewart, M.T. 2017 Very-large-scale motions in rough-bed open-channel flow. J. Fluid Mech. 814, 416–429.CrossRefGoogle Scholar
Carstensen, S., Sumer, B.M. & Fredsøe, J. 2010 Coherent structures in wave boundary layers. Part 1. Oscillatory motion. J. Fluid Mech. 646, 169–206.CrossRefGoogle Scholar
Clauser, F.H. 1956 The turbulent boundary layer. Adv. Appl. Maths 4, 1–51.Google Scholar
Davies, A.G., Soulsby, R.L. & King, H.L. 1988 A numerical model of the combined wave and current bottom boundary layer. J. Geophys. Res. 93 (C1), 491–508.CrossRefGoogle Scholar
De Jesus Henriques, T.A., Tedds, S.C., Botsari, A., Najafian, G., Hedges, T.S., Sutcliffe, C.J., Owen, I. & Poole, R.J. 2014 The effects of wave–current interaction on the performance of a model horizontal axis tidal turbine. Intl J. Mar. Energy 8, 17–35.CrossRefGoogle Scholar
De Souza Machado, A.A., Spencer, K., Kloas, W., Toffolon, M. & Zarfl, C. 2016 Metal fate and effects in estuaries: a review and conceptual model for better understanding of toxicity. Sci. Total Environ. 541, 268–281.CrossRefGoogle Scholar
Dean, R.G. & Dalrymple, R.A. 1991 Water Wave Mechanics for Engineers and Scientists. World Scientific.CrossRefGoogle Scholar
Deng, B.Q., Yang, Z., Xuan, A. & Shen, L. 2019 Influence of Langmuir circulations on turbulence in the bottom boundary layer of shallow water. J. Fluid Mech. 861, 275–308.CrossRefGoogle Scholar
Deng, B.Q., Yang, Z., Xuan, A. & Shen, L. 2020 Localizing effect of Langmuir circulations on small-scale turbulence in shallow water. J. Fluid Mech. 893, A6.CrossRefGoogle Scholar
Dogan, E., Örlü, R., Gatti, D., Vinuesa, R. & Schlatter, P. 2019 Quantification of amplitude modulation in wall-bounded turbulence. Fluid Dyn. Res. 51 (1), 011408.CrossRefGoogle Scholar
Draycott, S., Sellar, B., Davey, T., Noble, D.R., Venugopal, V. & Ingram, D.M. 2019 Capture and simulation of the ocean environment for offshore renewable energy. Renew. Sust. Energ. Rev. 104, 15–29.CrossRefGoogle Scholar
Duan, Y., Chen, Q., Li, D. & Zhong, Q. 2020 Contributions of very large-scale motions to turbulence statistics in open channel flows. J. Fluid Mech. 892, A3.CrossRefGoogle Scholar
Dyer, K.R. & Soulsby, R.L. 1988 Sand transport on the continental shelf. Annu. Rev. Fluid Mech. 20 (1), 295–324.CrossRefGoogle Scholar
Escudier, M.P., Nickson, A.K. & Poole, R.J. 2009 Turbulent flow of viscoelastic shear-thinning liquids through a rectangular duct: quantification of turbulence anisotropy. J. Non-Newtonian Fluid Mech. 160 (1), 2–10.CrossRefGoogle Scholar
Fagherazzi, S., Edmonds, D.A., Nardin, W., Leonardi, N., Canestrelli, A., Falcini, F., Jerolmack, D.J, Mariotti, G., Rowland, J.C. & Slingerland, R.L. 2015 Dynamics of river mouth deposits. Rev. Geophys. 53 (3), 642–672.CrossRefGoogle Scholar
Fagherazzi, S., et al. 2012 Numerical models of salt marsh evolution: ecological, geomorphic, and climatic factors. Rev. Geophys. 50 (1), RG1002.CrossRefGoogle Scholar
Flandrin, P., Rilling, G. & Goncalves, P. 2004 Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 11 (2), 112–114.CrossRefGoogle Scholar
Franca, M.J. & Brocchini, M. 2015 Turbulence in rivers. In Rivers–Physical, Fluvial and Environmental Processes (ed. P. Rowiński & A. Radecki-Pawlik), pp. 51–78. Springer.CrossRefGoogle Scholar
Francalanci, S., Bendoni, M., Rinaldi, M. & Solari, L. 2013 Ecomorphodynamic evolution of salt marshes: experimental observations of bank retreat processes. Geomorphology 195, 53–65.CrossRefGoogle Scholar
Fredsøe, J., Andersen, K.H. & Sumer, B.M. 1999 Wave plus current over a ripple-covered bed. Coast. Engng 38 (4), 177–221.CrossRefGoogle Scholar
Gaurier, B., Davies, P., Deuff, A. & Germain, G. 2013 Flume tank characterization of marine current turbine blade behaviour under current and wave loading. Renew. Energy 59, 1–12.CrossRefGoogle Scholar
Grant, W.D. & Madsen, O.S. 1979 Combined wave and current interaction with a rough bottom. J. Geophys. Res. 84 (C4), 1797–1808.CrossRefGoogle Scholar
Green, M.O & Coco, G. 2014 Review of wave–driven sediment resuspension and transport in estuaries. Rev. Geophys. 52 (1), 77–117.CrossRefGoogle Scholar
Grosch, C.E., Ward, L.W. & Lukasik, S.J. 1960 Viscous dissipation of shallow water waves. Phys. Fluids 3 (3), 477–479.CrossRefGoogle Scholar
Guasto, J.S., Rusconi, R. & Stocker, R. 2012 Fluid mechanics of planktonic microorganisms. Annu. Rev. Fluid Mech. 44, 373–400.CrossRefGoogle Scholar
Hackett, E.E., Luznik, L., Nayak, A.R., Katz, J. & Osborn, T.R. 2011 Field measurements of turbulence at an unstable interface between current and wave bottom boundary layers. J. Geophys. Res. 116 (C2), C02022.Google Scholar
Hedges, T.S. 1995 Regions of validity of analytical wave theories. In Proceedings of the Institution of Civil Engineers–Water, Maritime and Energy, pp. 111–114.Google Scholar
Huang, N.E., Shen, Z. & Long, S.R. 1999 A new view of nonlinear water waves: the Hilbert spectrum. Annu. Rev. Fluid Mech. 31 (1), 417–457.CrossRefGoogle Scholar
Huang, N.E., Shen, Z., Long, S.R., Wu, M.C., Shih, H.H., Zheng, Q., Yen, N.C., Tung, C.C. & Liu, H.H. 1998 The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 454 (1971), 903–995.CrossRefGoogle Scholar
Huang, N.E., Wu, M.C., Long, S.R., Shen, S.S.P., Qu, W., Gloersen, P. & Fan, K.L. 2003 A confidence limit for the empirical mode decomposition and Hilbert spectral analysis. Proc. R. Soc. Lond. A 459 (2037), 2317–2345.CrossRefGoogle Scholar
Huang, Y.X., Schmitt, F.G., Lu, Z.M., Fougairolles, P., Gagne, Y. & Liu, Y.L. 2010 Second-order structure function in fully developed turbulence. Phys. Rev. E 82 (2), 026319.CrossRefGoogle ScholarPubMed
Huang, Y.X., Schmitt, F.G., Lu, Z.M. & Liu, Y.L. 2008 An amplitude-frequency study of turbulent scaling intermittency using empirical mode decomposition and Hilbert spectral analysis. Europhys. Lett. 84 (4), 40010.CrossRefGoogle Scholar
Huang, Z. & Mei, C.C. 2003 Effects of surface waves on a turbulent current over a smooth or rough seabed. J. Fluid Mech. 497, 253–287.CrossRefGoogle Scholar
Huang, Z. & Mei, C.C. 2006 Wave-induced longitudinal vortices in a shallow current. J. Fluid Mech. 551, 323–356.CrossRefGoogle Scholar
Hunt, J.N. 1952 Viscous damping of waves over an inclined bed in a channel of finite width. La Houille Blanche 7, 836–842.CrossRefGoogle Scholar
Hussain, A.K.M.F. & Reynolds, W.C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41 (2), 241–258.CrossRefGoogle Scholar
Isaacson, M. 1991 Measurement of regular wave reflection. J. Waterways Port Coast. Ocean Engng 117 (6), 553–569.CrossRefGoogle Scholar
Kemp, P.H. & Simons, R.R. 1982 The interaction between waves and a turbulent current: waves propagating with the current. J. Fluid Mech. 116, 227–250.CrossRefGoogle Scholar
Kemp, P.H. & Simons, R.R. 1983 The interaction of waves and a turbulent current: waves propagating against the current. J. Fluid. Mech. 130, 73–89.CrossRefGoogle Scholar
Klopman, G. 1994 Vertical structure of the flow due to waves and currents – Laser-Doppler flow measurements for waves following or opposing a current. Progress Rep. No. H840-30. Part II, for Rijkswaterstaat (Tidal Hydraulic Division).Google Scholar
Lei, Y., Lin, J., He, Z. & Zuo, M.J. 2013 A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal. Pr. 35 (1-2), 108–126.CrossRefGoogle Scholar
Li, M., Garrett, C. & Skyllingstad, E. 2005 A regime diagram for classifying turbulent large eddies in the upper ocean. Deep-Sea Res. I 52 (2), 259–278.CrossRefGoogle Scholar
Lodahl, C.R., Sumer, B.M. & Fredsøe, J. 1998 Turbulent combined oscillatory flow and current in a pipe. J. Fluid Mech. 373, 313–348.CrossRefGoogle Scholar
Madsen, O.S. & Grant, W.D. 1976 Quantitative description of sediment transport by waves. In Proceedings of the 15th International Conference on Coastal Engineering, pp. 1092–1112.Google Scholar
Manes, C., Poggi, D. & Ridolfi, L. 2011 Turbulent boundary layers over permeable walls: scaling and near-wall structure. J. Fluid Mech. 687, 141–170.CrossRefGoogle Scholar
Marino, M., Rabionet, I.C., Musumeci, R.E. & Foti, E. 2018 Reliability of pressure sensors to measure wave height in the shoaling region. In Proceedings of the 36th International Conference on Coastal Engineering, vol. 36, paper 10.Google Scholar
Marusic, I., McKeon, B.J., Monkewitz, P.A., Nagib, H.M., Smits, A.J. & Sreenivasan, K.R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.CrossRefGoogle Scholar
McWilliams, J.C., Sullivan, P.P. & Moeng, C.H. 1997 Langmuir turbulence in the ocean. J. Fluid Mech. 334, 1–30.CrossRefGoogle Scholar
Monismith, S.G. 2020 Stokes drift: theory and experiments. J. Fluid Mech. 884, F1.CrossRefGoogle Scholar
Myrhaug, D. 1984 A theoretical model of combined wave and current boundary layers near a rough sea bottom. In Proceedings of the 3rd Offshore Mechanics and Arctic Engineering, pp. 559–568.Google Scholar
Nagib, H.M. & Chauhan, K.A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20 (10), 101518.CrossRefGoogle Scholar
Nayak, A.R., Li, C., Kiani, B.T. & Katz, J. 2015 On the wave and current interaction with a rippled seabed in the coastal ocean bottom boundary layer. J. Geophys. Res. 120 (7), 4595–4624.CrossRefGoogle Scholar
Nepf, H.M. & Monismith, S.G. 1991 Experimental study of wave-induced longitudinal vortices. J. Hydraul. Engng 117 (12), 1639–1649.CrossRefGoogle Scholar
Nezu, I. & Nakagawa, H. 1993 Turbulence in Open-Channel Flows. A. A. Balkema.Google Scholar
Nickels, T.B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M.S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. A 365 (1852), 807–822.Google ScholarPubMed
Nielsen, P. 1992 Coastal Bottom Boundary Layers and Sediment Transport. World Scientific.CrossRefGoogle Scholar
Nikora, V.I. & Goring, D. 2000 Eddy convection velocity and Taylor's hypothesis of'frozen’turbulence in a rough-bed open-channel flow. J. Hydrosci. Hydraul. Engng 18 (2), 75–91.Google Scholar
Noble, D.R., Draycott, S., Nambiar, A., Sellar, B.G., Steynor, J. & Kiprakis, A. 2020 Experimental assessment of flow, performance, and loads for tidal turbines in a closely-spaced array. Energies 13 (8), 1977.CrossRefGoogle Scholar
Olabarrieta, M., Medina, R. & Castanedo, S. 2010 Effects of wave–current interaction on the current profile. Coast. Engng 57 (7), 643–655.CrossRefGoogle Scholar
Peruzzi, C. 2020 Turbulence properties of smooth-bed open-channel flows with and without collinear gravity waves. PhD thesis, Politecnico di Torino.Google Scholar
Peruzzi, C., Poggi, D., Ridolfi, L. & Manes, C. 2020 On the scaling of large-scale structures in smooth-bed turbulent open-channel flows. J. Fluid Mech. 889, A1.CrossRefGoogle Scholar
Poggi, D., Porporato, A. & Ridolfi, L. 2002 An experimental contribution to near-wall measurements by means of a special Laser Doppler Anemometry technique. Exp. Fluids 32 (3), 366–375.CrossRefGoogle Scholar
Poggi, D., Porporato, A. & Ridolfi, L. 2003 Analysis of the small-scale structure of turbulence on smooth and rough walls. Phys. Fluids 15 (1), 35–46.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent flows. IOP Publishing.CrossRefGoogle Scholar
Qiao, F., Yuan, Y., Deng, J., Dai, D. & Song, Z. 2016 Wave–turbulence interaction-induced vertical mixing and its effects in ocean and climate models. Phil. Trans. R. Soc. Lond. A 374 (2065), 20150201.Google ScholarPubMed
Rato, R.T., Ortigueira, M.D. & Batista, A.G. 2008 On the HHT, its problems, and some solutions. Mech. Syst. Signal. Pr. 22 (6), 1374–1394.CrossRefGoogle Scholar
Robinson, A., Ingram, D., Bryden, I. & Bruce, T. 2015 The effect of inlet design on the flow within a combined waves and current flumes, test tank and basins. Coast. Engng 95, 117–129.CrossRefGoogle Scholar
Roy, S., Debnath, K. & Mazumder, B.S. 2017 Distribution of eddy scales for wave current combined flow. Appl. Ocean Res. 63, 170–183.CrossRefGoogle Scholar
Roy, S., Samantaray, S.S. & Debnath, K. 2018 Study of turbulent eddies for wave against current. Ocean Engng 150, 176–193.CrossRefGoogle Scholar
Schmitt, F.G., Huang, Y.X., Lu, Z.M., Liu, Y.L. & Fernandez, N. 2009 Analysis of velocity fluctuations and their intermittency properties in the surf zone using empirical mode decomposition. J. Mar. Syst. 77 (4), 473–481.CrossRefGoogle Scholar
Sellar, B.G., Wakelam, G., Sutherland, D.R.J., Ingram, D.M. & Venugopal, V. 2018 Characterisation of tidal flows at the European marine energy centre in the absence of ocean waves. Energies 11 (1), 176.CrossRefGoogle Scholar
Shaw, W.J. & Trowbridge, J.H. 2001 The direct estimation of near-bottom turbulent fluxes in the presence of energetic wave motions. J. Atmos. Ocean. Technol. 18 (9), 1540–1557.2.0.CO;2>CrossRefGoogle Scholar
Singh, S.K. & Debnath, K. 2016 Combined effects of wave and current in free surface turbulent flow. Ocean Engng 127, 170–189.CrossRefGoogle Scholar
Sinha, N., Tejada-Martínez, A.E., Akan, C. & Grosch, C.E. 2015 Toward a K-profile parameterization of Langmuir turbulence in shallow coastal shelves. J. Phys. Oceanogr. 45 (12), 2869–2895.CrossRefGoogle Scholar
Soulsby, R.L., Hamm, L., Klopman, G., Myrhaug, D., Simons, R.R. & Thomas, G.P. 1993 Wave-current interaction within and outside the bottom boundary layer. Coast. Engng 21 (1–3), 41–69.CrossRefGoogle Scholar
Sumer, B.M. 2014 Flow–structure–seabed interactions in coastal and marine environments. J. Hydraul Res. 52 (1), 1–13.CrossRefGoogle Scholar
Sumer, B.M., Petersen, T.U., Locatelli, L., Fredsøe, J., Musumeci, R.E. & Foti, E. 2013 Backfilling of a scour hole around a pile in waves and current. J. Waterways Port Coast. Ocean Engng 139 (1), 9–23.CrossRefGoogle Scholar
Tabrizi, A.A., Garibaldi, L., Fasana, A. & Marchesiello, S. 2014 Influence of stopping criterion for sifting process of empirical mode decomposition (EMD) on roller bearing fault diagnosis. In Advances in Condition Monitoring of Machinery in Non-Stationary Operations (G. Dalpiaz, R. Rubini, G. D'Elia, M. Cocconcelli, F. Chaari, R. Zimroz, W. Bartelmus & M. Haddar), pp. 389–398. Springer.CrossRefGoogle Scholar
Tambroni, N., Blondeaux, P. & Vittori, G. 2015 A simple model of wave–current interaction. J. Fluid Mech. 775, 328–348.CrossRefGoogle Scholar
Taylor, G.I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164 (919), 476–490.Google Scholar
Tejada-Martínez, A.E. & Grosch, C.E. 2007 Langmuir turbulence in shallow water. Part 2. Large-eddy simulation. J. Fluid Mech. 576, 63–108.CrossRefGoogle Scholar
Tejada-Martínez, A.E., Grosch, C.E., Sinha, N., Akan, C. & Martinat, G. 2012 Disruption of the bottom log layer in large-eddy simulations of full-depth Langmuir circulation. J. Fluid Mech. 699, 79–93.CrossRefGoogle Scholar
Umeyama, M. 2005 Reynolds stresses and velocity distributions in a wave-current coexisting environment. J. Waterways Port Coast. Ocean Engng 131 (5), 203–212.CrossRefGoogle Scholar
Umeyama, M. 2009 a Changes in turbulent flow structure under combined wave-current motions. J. Waterways Port Coast. Ocean Engng 135 (5), 213–227.CrossRefGoogle Scholar
Umeyama, M. 2009 b Mean velocity changes due to interaction between bichromatic waves and a current. J. Waterways Port Coast. Ocean Engng 135 (1), 11–23.CrossRefGoogle Scholar
Van Hoften, J.D.A. & Karaki, S. 1976 Interaction of waves and a turbulent current. In Proceedings of the 15th International Conference on Coastal Engineering, pp. 404–422.Google Scholar
Vettori, D. 2016 Hydrodynamic performance of seaweed farms: an experimental study at seaweed blade scale. PhD thesis, University of Aberdeen.Google Scholar
Xuan, A., Deng, B.Q. & Shen, L. 2019 Study of wave effect on vorticity in Langmuir turbulence using wave-phase-resolved large-eddy simulation. J. Fluid Mech. 875, 173–224.CrossRefGoogle Scholar
Yaglom, A.M. 1979 Similarity laws for constant-pressure and pressure-gradient turbulent wall flows. Annu. Rev. Fluid Mech. 11 (1), 505–540.CrossRefGoogle Scholar
Yuan, J. & Madsen, O.S. 2015 Experimental and theoretical study of wave–current turbulent boundary layers. J. Fluid Mech. 765, 480–523.CrossRefGoogle Scholar
Zampiron, A., Cameron, S. & Nikora, V.I. 2020 Secondary currents and very-large-scale motions in open-channel flow over streamwise ridges. J. Fluid Mech. 887, A17.CrossRefGoogle Scholar
Zhang, X. & Simons, R.R. 2019 Experimental investigation on the structure of turbulence in the bottom wave-current boundary layers. Coast. Engng 152, 103511.CrossRefGoogle Scholar