Published online by Cambridge University Press: 19 October 2018
Linear disturbance development in the von Kármán boundary layer on an infinite rotating-disc is investigated for an extensive range of azimuthal mode numbers  $n$. The study expands upon earlier investigations that were limited to those values of
$n$. The study expands upon earlier investigations that were limited to those values of  $n$ located near the onset of absolute instability (Lingwood, J. Fluid Mech., vol. 299, 1995, pp. 17–33), where disturbances to the genuine inhomogeneous flow were shown to be globally stable (Davies & Carpenter, J. Fluid Mech., vol. 486, 2003, pp. 287–329). Numerical simulations corresponding to azimuthal mode numbers greater than the conditions for critical absolute instability display a form of global linear instability that is characterised by a faster than exponential temporal growth, similar in appearance to that found on the rotating-disc with mass suction (Thomas & Davies, J. Fluid Mech., vol. 724, 2010, pp. 510–526) and other globally unstable flows (Huerre & Monkewitz, Annu. Rev. Fluid Mech., vol. 22, 1990, pp. 473–537). Solutions indicate that a change in the global behaviour arises for
$n$ located near the onset of absolute instability (Lingwood, J. Fluid Mech., vol. 299, 1995, pp. 17–33), where disturbances to the genuine inhomogeneous flow were shown to be globally stable (Davies & Carpenter, J. Fluid Mech., vol. 486, 2003, pp. 287–329). Numerical simulations corresponding to azimuthal mode numbers greater than the conditions for critical absolute instability display a form of global linear instability that is characterised by a faster than exponential temporal growth, similar in appearance to that found on the rotating-disc with mass suction (Thomas & Davies, J. Fluid Mech., vol. 724, 2010, pp. 510–526) and other globally unstable flows (Huerre & Monkewitz, Annu. Rev. Fluid Mech., vol. 22, 1990, pp. 473–537). Solutions indicate that a change in the global behaviour arises for 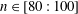 $n\in [80:100]$ that is marginally greater than those disturbances studied previously. Furthermore, the Reynolds number associated with the larger azimuthal mode numbers coincides with the upper bound of experimental predictions for transition. Thus, the local–global linear stability of the infinite rotating-disc is similar to the scenario outlined by Huerre & Monkewitz (1990) that states a region of local absolute instability is necessary but not sufficient for global instability to ensue. Conditions are derived to predict the azimuthal mode number needed to bring about a change in global behaviour, based on solutions of the linearised complex Ginzburg–Landau equation coupled with numerical simulations of disturbances to the radially homogeneous flow. The long term response is governed by a detuning effect, based on radial variations of the temporal frequency and matching shifts in temporal growth that increases for larger
$n\in [80:100]$ that is marginally greater than those disturbances studied previously. Furthermore, the Reynolds number associated with the larger azimuthal mode numbers coincides with the upper bound of experimental predictions for transition. Thus, the local–global linear stability of the infinite rotating-disc is similar to the scenario outlined by Huerre & Monkewitz (1990) that states a region of local absolute instability is necessary but not sufficient for global instability to ensue. Conditions are derived to predict the azimuthal mode number needed to bring about a change in global behaviour, based on solutions of the linearised complex Ginzburg–Landau equation coupled with numerical simulations of disturbances to the radially homogeneous flow. The long term response is governed by a detuning effect, based on radial variations of the temporal frequency and matching shifts in temporal growth that increases for larger  $n$, eventually attaining values sufficient to engineer global linear instability. The analysis is extended to include mass transfer through the disc surface, with similar conclusions drawn for disturbances to large enough azimuthal mode numbers. Finally, we conclude that the high
$n$, eventually attaining values sufficient to engineer global linear instability. The analysis is extended to include mass transfer through the disc surface, with similar conclusions drawn for disturbances to large enough azimuthal mode numbers. Finally, we conclude that the high  $n$ modes are unlikely to have a strong influence on disturbance development and transition in the von Kármán flow, as they will be unable to establish themselves across an extended radial range before nonlinear effects are triggered by the huge growth associated with the wavepacket maxima of the lower
$n$ modes are unlikely to have a strong influence on disturbance development and transition in the von Kármán flow, as they will be unable to establish themselves across an extended radial range before nonlinear effects are triggered by the huge growth associated with the wavepacket maxima of the lower  $n$-valued convective instabilities.
$n$-valued convective instabilities.