Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-19T17:46:06.622Z Has data issue: false hasContentIssue false
  • English
  • Français

On the generation of lift forces in random soft porous media

Published online by Cambridge University Press:  25 January 2009

P. MIRBOD ,
Y. ANDREOPOULOS  and
S. WEINBAUM
P. MIRBOD
Affiliation:
Departments of Biomedical and Mechanical Engineering, The City College of the City University of New York, New York, NY 10031, USA
Y. ANDREOPOULOS
Affiliation:
Departments of Biomedical and Mechanical Engineering, The City College of the City University of New York, New York, NY 10031, USA
S. WEINBAUM*
Affiliation:
Departments of Biomedical and Mechanical Engineering, The City College of the City University of New York, New York, NY 10031, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we examine the generation of pressure and lift forces in a random soft fibrous media layer that is confined between two planar surfaces, an infinite horizontal lower boundary and a horizontal inclined upper boundary, in the lubrication limit where the characteristic thickness of the fibre layer H ≪ L the length of the inclined surface. The model for the fibre layer is a Brinkman equation and the Darcy permeability Kp is described by the widely used Carman–Kozeny equation for random porous media. Two cases are considered: (a) an inclined upper boundary which slides freely on top of a stationary fibre layer which is firmly attached to the lower boundary and (b) an inclined stationary upper boundary with an attached fibre layer in which the horizontal lower boundary slides freely in its own plane beneath it. Superficially, the problems appear equivalent to the classical problem for a slider bearing where the solutions for the pressure distribution and lift force are independent of which boundary is moving. In this problem there is an optimum compression ratio k = h1/h2 = 2.2, where h1 and h2 are the heights at the leading and trailing edges, for maximum lift force. However, this symmetry is lost if the intervening space is filled with a soft porous fibrous material since the Brinkman equation is not invariant under a transformation of coordinates in which the inherently unsteady problem in case (a) is transformed to a steady reference frame in which the inclined upper boundary is stationary and the horizontal boundary with the adhered fibre layer moves below it. Although in the steady reference frame case (a) now appears to resemble case (b), the solutions are strikingly different and depend critically on the value of the dimensionless fibre interaction layer thickness 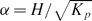. For α ≪ 1 the solutions for both cases approach the classical solution for a slider bearing. For α ≫ 1 we show, using asymptotic analysis that the solutions diverge dramatically. In case (a) the pressure and lift force increase as α2 and asymptotically approach a limiting behaviour for large values of α, first predicted in Feng and Weinbaum (J. Fluid Mech., vol. 422, 2000, p. 288), while in case (b) the pressure and lift force decay as α−2 since the inclined upper boundary is screened by the fibre layer and the amount of fluid dragged through the fluid gap decreases as α increases and vanishes for α ≫ 1. The solution in case (a), where the inclined upper boundary moves, is of particular interest since it reveals the potential to generate enormous lift forces using commercially available inexpensive soft porous materials provided the lateral leakage at the edge of the planform can be eliminated through the use of a channel with impermeable sidewalls as first proposed in the work by Wu, Andreopolous and Weinbaum (Phys. Rev. Lett., vol. 93, 2004, p. 194501). The behaviour is illustrated for both a toboggan sliding in such a channel and a larger planform that might be useful in commercial transportation.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 619 , 25 January 2009 , pp. 147 - 166
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Brinkman, H. C. 1947 A calculation of the viscous force exerted by a flowing fluid in a dense swarm of particles. Appl. Sci. Res. A 1, 27–34.CrossRefGoogle Scholar
Chien, S., Usami, S. & Skalak, R. 1984 Blood flow in small tubes. In Handbook of Physiology, Circulation. Section on Microcirculation (ed. Renkin, E. M. & Michel, C.), pp. 217–249. American Physiological Society.Google Scholar
Damiano, E. R. 1998 The effect of the endothelial-cell glycocalyx on the motion of red blood cells through capillaries. Microvasc. Res. 55, 77–91.CrossRefGoogle ScholarPubMed
Damiano, E. R. & Stace, T. M. 2002 A mechano-electrochemical model of radial deformation of the capillary glycocalyx. Biophys. J. 82, 1153–1175.CrossRefGoogle ScholarPubMed
Feng, J. & Weinbaum, S. 2000 Lubrication theory in highly compressible porous media: the mechanics of skiing, from red cells to humans. J. Fluid Mech. 422, 288–317.CrossRefGoogle Scholar
Han, Y., Ganatos, P. & Weinbaum, S. 2005 Transmission of steady and oscillatory fluid shear stress across epithelial and endothelial surface layers. Phys. Fluids 17, 031508(1–13).CrossRefGoogle Scholar
Han, Y., Weinbaum, S., Spaan, J. A. E. & Vink, H. 2006 Large-deformation analysis of the elastic recoil of fibre layers in a Brinkman medium with application to the endothelial glycocalyx. J. Fluid Mech. 554, 217–235.CrossRefGoogle Scholar
Happel, J. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media. Springer.CrossRefGoogle Scholar
Mirbod, P., Andreopoulos, Y. & Weinbaum, S. An airborne jet train that flies on a soft porous track. Proc. Natl. Acad. Sci. in press.Google Scholar
Pries, A. R., Secomb, T. W. & Gaehtgens, P. 2000 The endothelial surface layer. Pflugers Arch. 440, 653–666.CrossRefGoogle ScholarPubMed
Pries, A. R., Secomb, T. W., Gessner, T., Sperandio, M. B., Gross, J. F. & Gaehtgens, P. 1994 Resistance to blood flow in microvessels in vivo. Circ. Res. 75, 904–915.CrossRefGoogle ScholarPubMed
Roy, B. C. & Damiano, E. R. 2008 On the motion of a porous sphere in a Stokes flow parallel to a planar confining boundary. J. Fluid Mech. 606, 75–104.CrossRefGoogle Scholar
Sangani, A. S. & Acrivos, A. 1982 Slow flow past periodic arrays of cylinders with application to heat transfer. Intl J. Multiphase Flow 8, 193–206.CrossRefGoogle Scholar
Schlichting, H. 1979 Boundary Layer Theory, sixth edn.McGraw-Hill.Google Scholar
Secomb, T. W., Hsu, R. & Pries, A. R. 1998 A model for red blood cell motion in glycocalyx-lined capillaries. Am. J. Physiol. Heart Ciric. Physiol. 274, H1016–H1022.CrossRefGoogle Scholar
Secomb, T. W., Hsu, R. & Pries, A. R. 2001 Motion of red blood cells in a capillary with an endothelial surface layer: effect of flow velocity. Am. J. Physiol. Heart Circ. Physiol. 281, H629–H636.CrossRefGoogle Scholar
Thi, M. M., Tarbell, J. M., Weinbaum, S. & Spray, C. D. 2004 The role of the glycocalyx in reorganization of the actin cytoskeleton under fluid shear stress: A “bumper-car” model. Proc. Natl. Acad. Sci. 101, 16483–16488.CrossRefGoogle Scholar
Truskey, G. A., Yuan, F. & Katz, D. F. 2004 Transport Phenomena in Biological Systems. Prentice Hall.Google Scholar
Vink, H. & Duling, B. R. 1996 Identification of distinct luminal domains for macromolecules, erythrocytes and leukocytes within mammalian capillaries. Circ. Res. 71, 581–589.CrossRefGoogle Scholar
Weinbaum, S., Tarbell, J. M. & Damiano, E. R. 2007 The structure and function of the endothelial glycocalyx layer. Annu. Rev. Biomed. Eng. 9, 121–167.CrossRefGoogle ScholarPubMed
Weinbaum, S., Zhang, X., Han, Y., Vink, H. & Cowin, S. 2003 Mechanotransduction and flow across the endothelial glycocalyx. Proc. Natl. Acad. Sci. 100, 7988–7996.CrossRefGoogle ScholarPubMed
Wu, Q., Andreopolous, Y. & Weinbaum, S. 2004 From red cells to snowboarding: a new concept for a train track. Phys. Rev. Lett. 93 (19), 194501.CrossRefGoogle ScholarPubMed
Wu, Q., Andreopoloulos, Y., Xanthos, S. & Weinbaum, S. 2005 Dynamic compression of highly compressible porous media with application to snow compaction. J. Fluid Mech. 542, 281–304.CrossRefGoogle Scholar
Wu, Q., Igci, Y., Andreopoulos, Y. & Weinbaum, S. 2006 Lift mechanics of downhill skiing and snowboarding. Med. Sci. Sports Exer. 38 (6), 1132–1146.CrossRefGoogle ScholarPubMed