On the flux Richardson number in stably stratified turbulence

Abstract

The flux Richardson number 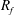$R_{f}$ (often referred to as the mixing efficiency) is a widely used parameter in stably stratified turbulence which is intended to provide a measure of the amount of turbulent kinetic energy 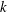$k$ that is irreversibly converted to background potential energy (which is by definition the minimum potential energy that a stratified fluid can attain that is not available for conversion back to kinetic energy) due to turbulent mixing. The flux Richardson number is traditionally defined as the ratio of the buoyancy flux 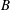$B$ to the production rate of turbulent kinetic energy 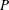$P$. An alternative generalized definition for 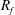$R_{f}$ was proposed by Ivey & Imberger (J. Phys. Oceanogr., vol. 21, 1991, pp. 650–658), where the non-local transport terms as well as unsteady contributions were included as additional sources to the production rate of 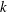$k$. While this definition precludes the need to assume that turbulence is statistically stationary, it does not properly account for countergradient fluxes that are typically present in more strongly stratified flows. Hence, a third definition that more rigorously accounts for only the irreversible conversions of energy has been defined, where only the irreversible fluxes of buoyancy and production (i.e. the dissipation rates of 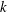$k$ and turbulent potential energy (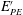$E_{PE}^{\prime }$)) are used. For stationary homogeneous shear flows, all of the three definitions produce identical results. However, because stationary and/or homogeneous flows are typically not found in realistic geophysical situations, clarification of the differences/similarities between these various definitions of 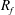$R_{f}$ is imperative. This is especially true given the critical role 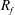$R_{f}$ plays in inferring turbulent momentum and heat fluxes using indirect methods, as is commonly done in oceanography, and for turbulence closure parameterizations. To this end, a careful analysis of two existing direct numerical simulation (DNS) datasets of stably stratified homogeneous shear and channel flows was undertaken in the present study to compare and contrast these various definitions. We find that all three definitions are approximately equivalent when the gradient Richardson number 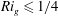$Ri_{g}\leqslant 1/4$. Here, 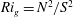$Ri_{g}=N^{2}/S^{2}$, where 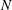$N$ is the buoyancy frequency and 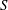$S$ is the mean shear rate, provides a measure of the stability of the flow. However, when 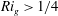$Ri_{g}>1/4$, significant differences are noticeable between the various definitions. In addition, the irreversible formulation of 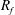$R_{f}$ based on the dissipation rates of 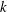$k$ and 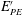$E_{PE}^{\prime }$ is the only definition that is free from oscillations at higher gradient Richardson numbers. Both the traditional definition and the generalized definition of 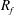$R_{f}$ exhibit significant oscillations due to the persistence of linear internal wave motions and countergradient fluxes that result in reversible exchanges between 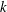$k$ and 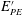$E_{PE}^{\prime }$. Finally, we present a simple parameterization for the irreversible flux Richardson number 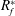$R_{f}^{\ast }$ based on 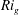$Ri_{g}$ that produces excellent agreement with the DNS results for 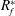$R_{f}^{\ast }$.