Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T02:32:28.704Z Has data issue: false hasContentIssue false
  • English
  • Français

On the flow of buoyant fluid injected into an aquifer with a background flow

Published online by Cambridge University Press:  12 July 2012

Iain Gunn  and
Andrew W. Woods
Iain Gunn
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods*
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the dispersal of a plume of incompressible buoyant fluid injected into a confined inclined aquifer in which there is a background flow. We assume that, to prevent pressure buildup in the system, there is an outflow from the aquifer, with flux equal to the injection flux, through a producing well. Using the method of characteristics, we identify that the trajectory of the plume of injected fluid depends on the magnitudes of both the injection flux 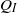and the background aquifer flux 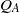relative to the buoyancy-driven exchange flow of injected and original fluid within the aquifer 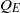, on the direction of the background aquifer flow, and on whether the producing well lies upslope or downslope from the injecting well. 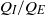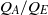We find the values of the controlling parameters and for which all injected fluid flows up-dip, for which the injected fluid partitions into a component moving up-dip and a component moving down-dip, and for which all injected fluid flows down-dip. A key learning from the analysis is that there may be very different plume trajectories when a buoyant fluid is injected into a confined, inclined aquifer, and prediction of the trajectory depends on knowledge of the background flow as well as the injection rate and location of the producing wells. In the process of 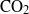sequestration, this range of initial plume geometries can inform analysis of longer-term geological storage and assessment of the risk of activating different possible leakage pathways to the surface.

JFM classification

Low-Reynolds-number flows: Porous media Geophysical and Geological Flows: Gravity currents Convection: Convection in porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 274 - 294
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Barenblatt, G. I. 1996 Dimensional Analysis, Self-Similarity and Intermediate Asymptotics. Cambridge University Press.CrossRefGoogle Scholar
2. Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover.Google Scholar
3. Bickle, M., Chadwick, A., Huppert, H. E., Hallworth, M. & Lyle, S. 2007 Modelling carbon dioxide accumulation at Sleipner: implications for underground carbon storage. Earth Planet. Sci. Lett. 255, 164–176.CrossRefGoogle Scholar
4. Cavanagh, A. & Ringrose, P. 2010 Salah high-resolution heterogeneous simulations of CO2 storage. Search and Discovery, 80092.Google Scholar
5. Farcas, A. & Woods, A. W. 2009 The effect of drainage on the capillary retention of in a layered permeable rock. J. Fluid Mech. 618, 349–359.CrossRefGoogle Scholar
6. Garven, G. 1995 Continental-scale groundwater flow and geologic processes. Annu. Rev. Earth Planet. Sci. 23, 89–117.CrossRefGoogle Scholar
7. Gunn, I. & Woods, A. W. 2011 On the flow of buoyant fluid injected into a confined, inclined aquifer. J. Fluid Mech. 672, 109–129.CrossRefGoogle Scholar
8. Hesse, M. A., Orr, F. M. Jr & Tchelepi, H. A. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.CrossRefGoogle Scholar
9.IPCC 2005 IPCC Special Report on Carbon Dioxide Capture and Storage. Cambridge University Press.Google Scholar
10. Juanes, R., MacMinn, C. W. & Szulczewski, M. L. 2010 The footprint of the plume during carbon dioxide storage in saline aquifers: storage efficiency for capillary trapping at the basin scale. Transp. Porous Med. 82, 19–30.CrossRefGoogle Scholar
11. Juanes, R. E., Spiteri, J., Orr, F. M. & Blunt, M. J. 2006 Impact of relative permeability hysteresis on geological storage. Water Resour. Res. 42, W12418.CrossRefGoogle Scholar
12. Mitchell, V. & Woods, A. W. 2006 Gravity driven flow in confined aquifers. J. Fluid Mech. 566, 345–355.CrossRefGoogle Scholar
13. Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404.CrossRefGoogle Scholar
14. Neufeld, J. A., Vella, D. & Huppert, H. E. 2009 The effect of a fissure on storage in a porous medium. J. Fluid Mech. 639, 239–259.CrossRefGoogle Scholar
15. Nordbotten, J. M. & Celia, M. A. 2006 Similarity solutions for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327.CrossRefGoogle Scholar
16. Nordbotten, J. M., Kavetski, D., Celia, M. A. & Bachu, S. 2009 Model for leakage including multiple geological layers and multiple leaky wells. Environ. Sci. Technol. 43, 739–749.CrossRefGoogle Scholar
17. Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1992 Numerical Recipes in Fortran 77. Cambridge University Press.Google Scholar
18. Pritchard, D. 2007 Gravity currents over fractured substrates in a porous medium. J. Fluid Mech. 584, 415–431.CrossRefGoogle Scholar
19. Pruess, K., Xu, T., Apps, J. & Garcia, J. 2003 Numerical modelling of aquifer disposal of . SPE J. 8 (1), 49–60.CrossRefGoogle Scholar
20. Vella, D. & Huppert, H. E. 2006 Gravity currents in a porous medium at an inclined plane. J. Fluid Mech. 555, 353–362.CrossRefGoogle Scholar
21. Verdon, J. & Woods, A. W. 2007 Gravity driven reacting flows in a confined porous aquifer. J. Fluid Mech. 588, 29–41.CrossRefGoogle Scholar
22. Woods, A. W. & Norris, S. 2010 On the role of caprock and fracture zones in dispersing gas plumes in the subsurface. Water Resour. Res. 46, W08522.CrossRefGoogle Scholar
23. Yortsos, Y. C. 1995 A theoretical analysis of vertical flow equilibrium. Trans. Porous Med. 18, 107–129.CrossRefGoogle Scholar