Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T06:45:09.476Z Has data issue: false hasContentIssue false
  • English
  • Français

On the evolution of the plume function and entrainment in the near-source region of lazy plumes

Published online by Cambridge University Press:  05 October 2017

G. Marjanovic ,
G. N. Taub  and
S. Balachandar Open the ORCID record for S. Balachandar [Opens in a new window]
G. Marjanovic*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA
G. N. Taub
Affiliation:
School of Mechanical and Materials Engineering, Washington State University, Everett, WA 98201, USA
S. Balachandar
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Plumes occur in many natural and industrial settings, such as chimney smoke, volcanic eruptions and deep water oil spills. A plume function, $\unicode[STIX]{x1D6E4}$, is used to characterize plumes and jets. The far-field behaviour of these flows has been studied in great detail while the near-field behaviour has not quite received the same attention. We examine near-field phenomena such as radial constriction, termed necking, and vortex structure formations with new high resolution direct numerical simulations. Four lazy plumes with increasing values of the source plume parameter, 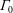$\unicode[STIX]{x1D6E4}_{0}$, are simulated. We study the evolution of entrainment and the plume function. The original assumptions, that Reynolds stresses dominate viscous shear stresses, do not hold for lazy plumes in the near field. Due to this, a deviation from self-similarity occurs initially and is corrected by a large entrainment coefficient caused by vortex stretching and compression. After correcting for the virtual origin, comparison between theory and simulations shows a monotonic decay of 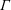$\unicode[STIX]{x1D6E4}$ towards pure plume behaviour. The entrainment coefficient asymptotes to a widely accepted constant value for plumes.

JFM classification

Convection: Convection Convection: Plumes/thermals Wakes/Jets: Shear layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 830 , 10 November 2017 , pp. 736 - 759
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, G. 1965 Entrainment principle and its restrictions to solve problems of jets. J. Hydraulic Res. 3 (2), 1–23.Google Scholar
Aissia, H. B., Zaouali, Y. & El Salem, G. 2002 Numerical study of the influence of dynamic and thermal exit conditions on axisymmetric laminar buoyant jet. Numer. Heat Transfer A 42, 427.CrossRefGoogle Scholar
Anwar, H. O. 1969 Experiment on an effluent discharging from a slot into stationary or slow moving fluid of greater density. J. Hydraulic Res. 7 (4), 411–431.CrossRefGoogle Scholar
Boersma, B. J., Brethouwer, G. & Nieuwstadt, F. T. M. 1998 A numerical investigation on the effect of the inflow conditions on the self-similar region of a round jet. Phys. Fluids 10, 899–909.Google Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2006 The route to self-similarity in turbulent jets and plumes. J. Fluid Mech. 547, 137–148.Google Scholar
Carlotti, P. & Hunt, G. R. 2017 An entrainment model for lazy turbulent plumes. J. Fluid Mech. 811, 682–700.Google Scholar
Caulfield, C. C.1991 Stratification and buoyancy in geophysical flows. PhD thesis, University of Cambridge, UK.Google Scholar
Caulfield, C. C. & Woods, A. W. 1995 Plumes with non-monotonic mixing behavior. Geophys. Astrophys. Fluid Dyn. 79, 173–199.Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.CrossRefGoogle Scholar
Chen, C. J. & Rodi, W. 1980 Vertical turbulent buoyant jets: a review of experimental data. NASA STI/Recon Tech. Rep. A 80, 21–58.Google Scholar
Citriniti, J. H. & George, W. K. 2000 Reconstruction of the global velocity field in the axisymmetric mixing layer utilizing the proper orthogonal decomposition. J. Fluid Mech. 418, 137–166.Google Scholar
Fiedler, H. E. 1988 Coherent structures in turbulent flows. Prog. Aerosp. Sci. 25 (3), 231–269.CrossRefGoogle Scholar
Fischer, H. B., List, E. J., Koh, R. C. Y., Imberger, J. & Brooks, N. H. 1979 Mixing in Coastal and Inland Waters. Academic.Google Scholar
Fox, D. G. 1970 Forced plume in a stratified fluid. J. Geophys. Res. 75 (33), 6818–6835.Google Scholar
George, W. K., Alpert, R. L. & Tamanini, F. 1977 Turbulence measurements in an axisymmetric buoyant plume. Intl J. Heat Mass Transfer 20 (11), 1145–1154.Google Scholar
Hargreaves, D. M., Scase, M. M. & Evans, I. 2012 A simplified computational analysis of turbulent plumes and jets. Environ. Fluid Mech. 12 (6), 555–578.Google Scholar
Harris, R. P.1999 Densimetric flows caused by the discharge of heated two-dimensional jets beneath a free surface. PhD thesis, University of Bristol.Google Scholar
Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.Google Scholar
Hunt, G. R. & Kaye, N. B. 2005 Lazy plumes. J. Fluid Mech. 533, 329–338.CrossRefGoogle Scholar
Kaminski, E., Tait, S. & Carazzo, G. 2005 Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 526, 361–376.Google Scholar
Kaye, N. B. 2008 Turbulent plumes in stratified environments: a review of recent work. Atmos.-Ocean 46 (4), 433–441.Google Scholar
Kaye, N. B. & Hunt, G. R. 2009 An experimental study of large area source turbulent plumes. Intl J. Heat Fluid Flow 30 (6), 1099–1105.Google Scholar
Kotsovinos, N. E.1975 A study of the entrainment and turbulence in a plane buoyant jet. PhD thesis, California Institute of Technology, Pasadena, California.Google Scholar
Lee, S. L. & Emmons, H. W. 1961 A study of natural convection above a line fire. J. Fluid Mech. 11 (03), 353–368.Google Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.Google Scholar
Matulka, A., López, P., Redondo, J. M. & Tarquis, A. 2014 On the entrainment coefficient in a forced plume: quantitative effects of source parameters. Nonlinear Process. Geophys. 21 (1), 269–278.CrossRefGoogle Scholar
Mcilwain, S. & Pollard, A. 2002 Large eddy simulation of the effects of mild swirl on the near field of a round free jet. Phys. Fluids 14 (2), 653–661.Google Scholar
Morton, B. R. 1959 Forced plumes. J. Fluid Mech. 5 (1), 151–163.Google Scholar
Morton, B. R. & Middleton, J. 1973 Scale diagrams for forced plumes. J. Fluid Mech. 58, 165–176.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. 234 (1196), 1–23.Google Scholar
Nakagome, H. & Hirata, M. 1977 The structure of turbulent diffusion in an axisymmetrical thermal plume. In Proc. 1976 ICHMT Seminar on Turbulent Buoyant Convection, pp. 361–372.Google Scholar
Papanicolaou, P. N. & List, E. J. 1987 Statistical and spectral properties of tracer concentration in round buoyant jets. Intl J. Heat Mass Transfer 30 (10), 2059–2071.Google Scholar
Papanicolaou, P. N. & List, E. J. 1988 Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 195, 341–391.Google Scholar
Pham, M. V., Plourde, F. & Doan, K. S. 2007 Direct and large-eddy simulations of a pure thermal plume. Phys. Fluids 19, 125103.Google Scholar
Pham, M. V., Plourde, F., Kim, S. D. & Balachandar, S. 2006 Large-eddy simulation of a pure thermal plume under rotating conditions. Phys. Fluids 18, 015101.CrossRefGoogle Scholar
Priestley, C. H. B. & Ball, F. K. 1955 Continuous convection from an isolated source of heat. Q. J. R. Meteorol. Soc. 81 (348), 144–157.Google Scholar
Railston, W. 1954 The temperature decay law of a naturally convected air stream. Proc. Phys. Soc. Section B 67 (1), 42.Google Scholar
van Reeuwijk, M. & Craske, J. 2015 Energy-consistent entrainment relations for jets and plumes. J. Fluid Mech. 782, 333–355.Google Scholar
van Reeuwijk, M., Salizzoni, P., Hunt, G. R. & Craske, J. 2016 Turbulent transport and entrainment in jets and plumes: a dns study. Phys. Rev. Fluids 1 (7), 074301.Google Scholar
Rouse, H., Yih, C. S. & Humphreys, H. W. 1952 Gravitational convection from a boundary source. Tellus 4, 201.Google Scholar
Schmidt, W. 1941 Turbulente ausbreitung eines stromes erhitzter luft. Z. Angew. Math. Mech. 21 (5), 265–278.Google Scholar
Shabbir, A. & George, W.K 1994 Experiments on a round turbulent buoyant plume. J. Fluid Mech. 275, 1–25.CrossRefGoogle Scholar
Taub, G. N., Lee, H., Balachandar, S. & Sherif, S. A. 2015 An examination of the high-order statistics of developing jets, lazy and forced plumes at various axial distances from their source. J. Turbul. 16 (10), 950–978.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Wang, H. & Law, A. W. K. 2002 Second-order integral model for a round turbulent buoyant jet. J. Fluid Mech. 459, 397–428.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vorticies in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar