Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T04:49:51.764Z Has data issue: false hasContentIssue false
  • English
  • Français

On the dispersion of a drug delivered intrathecally in the spinal canal

Published online by Cambridge University Press:  27 December 2018

J. J. Lawrence ,
W. Coenen Open the ORCID record for W. Coenen [Opens in a new window] ,
A. L. Sánchez Open the ORCID record for A. L. Sánchez [Opens in a new window] ,
G. Pawlak ,
C. Martínez-Bazán ,
V. Haughton  and
J. C. Lasheras
J. J. Lawrence
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, USA
W. Coenen
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, USA
A. L. Sánchez*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, USA
G. Pawlak
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, USA
C. Martínez-Bazán
Affiliation:
Department of Mechanical and Mining Engineering, University of Jaén, Spain
V. Haughton
Affiliation:
Department of Radiology, University of Wisconsin, USA
J. C. Lasheras
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, USA Department of Bioengineering, University of California San Diego, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates the transport of a solute carried by the cerebrospinal fluid (CSF) in the spinal canal. The analysis is motivated by the need for a better understanding of drug dispersion in connection with intrathecal drug delivery (ITDD), a medical procedure used for treatment of some cancers, infections and pain, involving the delivery of the drug to the central nervous system by direct injection into the CSF via the lumbar route. The description accounts for the CSF motion in the spinal canal, described in our recent publication (Sánchez et al., J. Fluid Mech., vol. 841, 2018, pp. 203–227). The Eulerian velocity field includes an oscillatory component with angular frequency 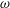$\unicode[STIX]{x1D714}$, equal to that of the cardiac cycle, and associated tidal volumes that are a factor 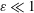$\unicode[STIX]{x1D700}\ll 1$ smaller than the total CSF volume in the spinal canal, with the small velocity corrections resulting from convective acceleration providing a steady-streaming component with characteristic residence times of order 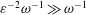$\unicode[STIX]{x1D700}^{-2}\unicode[STIX]{x1D714}^{-1}\gg \unicode[STIX]{x1D714}^{-1}$. An asymptotic analysis for 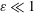$\unicode[STIX]{x1D700}\ll 1$ accounting for the two time scales 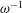$\unicode[STIX]{x1D714}^{-1}$ and 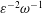$\unicode[STIX]{x1D700}^{-2}\unicode[STIX]{x1D714}^{-1}$ is used to investigate the prevailing drug-dispersion mechanisms and their dependence on the solute diffusivity, measured by the Schmidt number 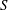$S$. Convective transport driven by the time-averaged Lagrangian velocity, obtained as the sum of the Eulerian steady-streaming velocity and the Stokes-drift velocity associated with the non-uniform pulsating flow, is found to be important for all values of $S$. By way of contrast, shear-enhanced Taylor dispersion, which is important for values of 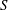$S$ of order unity, is shown to be negligibly small for the large values 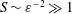$S\sim \unicode[STIX]{x1D700}^{-2}\gg 1$ corresponding to the molecular diffusivities of all ITDD drugs. Results for a model geometry indicate that a simplified equation derived in the intermediate limit $1\ll S\ll \unicode[STIX]{x1D700}^{-2}$ provides sufficient accuracy under most conditions, and therefore could constitute an attractive reduced model for future quantitative analyses of drug dispersion in the spinal canal. The results can be used to quantify dependences of the drug-dispersion rate on the frequency and amplitude of the pulsation of the intracranial pressure, the compliance and specific geometry of the spinal canal and the molecular diffusivity of the drug.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Biomedical flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 679 - 720
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhadelia, R. A., Bogdan, A. R., Kaplan, R. F. & Wolpert, S. M. 1997 Cerebrospinal fluid pulsation amplitude and its quantitative relationship to cerebral blood flow pulsations: a phase-contrast MR flow imaging study. Neuroradiology 39 (4), 258–264.Google Scholar
Blasberg, R. G., Patlak, C. & Fenstermacher, J. D. 1975 Intrathecal chemotherapy: brain tissue profiles after ventriculociternal perfusion. J. Pharmacol. Exp. Ther. 195, 73–83.Google Scholar
Borhani, N., Nelissen, R. M. & Buchser, E.2011 Fluid dynamics of drug spread in the intrathecal space. Neurohydrodynamics Working Group Meeting.Google Scholar
Bottros, M. M. & Christo, P. J. 2014 Current perspectives on intrathecal drug delivery. J. Pain Res. 7, 615–626.Google Scholar
du Boulay, G. H. 1966 Pulsatile movements in the CSF pathways. Br. J. Radiol. 39, 255–262.Google Scholar
Buchser, E., Durrer, A., Chdel, D. & Mustaki, J. 2004 Efficacy of intrathecal bupivacaine: How important is the flow rate? Pain Med. 5, 248–252.Google Scholar
Carpenter, P. W., Berkouk, K. & Lucey, A. D. 2003 Pressure wave propagation in fluid-filled co-axial elastic tubes. Part 2. Mechanisms for the pathogenesis of syringomyelia. J. Biomech. Engng 125 (6), 857–863.Google Scholar
Di Chiro, G. 1964 Movement of the cerebrospinal fluid in human beings. Nature 204, 290–291.Google Scholar
Dreha-Kulaczewski, S., Joseph, A. A., Merboldt, K. D., Ludwig, H. C., Gärtner, J. & Frahm, J. 2015 Inspiration is the major regulator of human CSF flow. J. Neurosci. 35 (6), 2485–2491.Google Scholar
Flack, S. H. & Bernards, C. M. 2010 Cerebrospinal fluid and spinal cord distribution of hyperbaric bupivacaine and baclofen during slow intrathecal infusion in pigs. Anesthesiology 112 (1), 165–173.Google Scholar
Grotberg, J. B. 1994 Pulmonary flow and transport phenomena. Annu. Rev. Fluid Mech. 26 (1), 529–571.Google Scholar
Hettiarachchi, H. D. M., Hsu, Y., Harris, T. J. & Linninger, A. A. 2011 The effect of pulsatile flow on intrathecal drug delivery in the spinal canal. Ann. Biomed. Engng 39 (10), 2592–2602.Google Scholar
Hsu, Y., Hettiarachchi, H. D. M., Zhu, D. C. & Linninger, A. A. 2012 The frequency and magnitude of cerebrospinal fluid pulsations influence intrathecal drug distribution: key factors for interpatient variability. Anesth. Analg. 115 (2), 386–394.Google Scholar
Hydon, P. E. & Pedley, T. J. 1993 Axial dispersion in a channel with oscillating walls. J. Fluid Mech. 249, 535–555.Google Scholar
Kalata, W., Martin, B. A., Oshinski, J. N., Jerosch-Herold, M., Royston, T. J. & Loth, F. 2009 MR measurement of cerebrospinal fluid velocity wave speed in the spinal canal. IEEE Trans. Biomed. Engng 56 (6), 1765–1768.Google Scholar
Kamran, S. & Wright, B. D. 2001 Complications of intrathecal drug delivery systems. Neuromodulation 4, 111–115.Google Scholar
Kao, Y. H., Guo, W. Y., Liou, A. J. K., Hsiao, Y. H. & Chou, C. C. 2008 The respiratory modulation of intracranial cerebrospinal fluid pulsation observed on dynamic echo planar images. Magn. Reson. Imaging 26 (2), 198–205.Google Scholar
Khani, M., Sass, L. R., Xing, T., Sharp, M. K., Balédent, O. & Martin, B. A. 2018 Anthropomorphic model of intrathecal cerebrospinal fluid dynamics within the spinal subarachnoid space: spinal cord nerve roots increase steady-streaming. J. Biomech. Engng 140 (8), 081012.Google Scholar
Kroin, J. S., Ali, A., York, M. & Penn, R. D. 1993 The distribution of medication along the spinal canal after chronic intrathecal administration. Neurosurgery 33 (2), 226–230.Google Scholar
Kurtcuoglu, V. 2011 Computational fluid dynamics for the assessment of cerebrospinal fluid flow and its coupling with cerebral blood flow. In Biomechanics of the Brain (ed. Miller, K.), pp. 169–188. Springer.Google Scholar
Lanz, E., Däubler, F., Eissner, D., Brod, K. H. & Theiss, D. 1986 Effect of spinal CSF dynamics on the subarachnoid diffusion of a substance applied close to the spinal cord. Reg. Anaesth. 9 (1), 4–8.Google Scholar
Larrieu, E., Hinch, E. J. & Charru, F. 2009 Lagrangian drift near a wavy boundary in a viscous oscillating flow. J. Fluid Mech. 630, 391–411.Google Scholar
Lee, Y. C., Hsieh, C. C., Chuang, J. P. & Li, C. Y. 2017 The necessity of intrathecal chemotherapy for the treatment of breast cancer patients with leptomeningeal metastasis: a systematic review and pooled analysis. Curr. Probl. Cancer 41, 355–370.Google Scholar
Linninger, A. A., Tangen, K., Hsu, C. Y. & Frim, D. 2016 Cerebrospinal fluid mechanics and its coupling to cerebrovascular dynamics. Annu. Rev. Fluid Mech. 48, 219–257.Google Scholar
Lynch, L. 2014 Intrathecal drug delivery systems. Contin. Educ. Anaesth. Crit. Care Pain 14, 27–31.Google Scholar
Marmarou, A., Shulman, K. & Lamorgese, J. 1975 Compartmental analysis of compliance and outflow resistance of the cerebrospinal fluid system. J. Neurosurg. 43 (5), 523–534.Google Scholar
Mokri, B. 2001 The Monro–Kellie hypothesis applications in CSF volume depletion. Neurology 56 (12), 1746–1748.Google Scholar
Nelissen, R. M.2008 Fluid mechanics of intrathecal drug delivery. PhD thesis, École Polytechnique Fédérale de Lausanne.Google Scholar
Onofrio, B. M., Yaksh, T. L. & Arnold, P. G. 1981 Continuous low-dose intrathecal morphine administration in the treatment of chronic pain of malignant origin. Mayo Clin. Proc. 56, 516–520.Google Scholar
Pardridge, W. M. 2011 Drug transport in brain via the cerebrospinal fluid. Fluids Barriers CNS 8, 7.Google Scholar
Penn, R. D. 2003 Intrathecal medication delivery. Neurosurg. Clin. N. Am. 14 (3), 381–387.Google Scholar
Pizzichelli, G.2016 Modelling approaches of innovative drug delivery strategies for the central nervous system. PhD thesis, Scuola Superiore Sant’Anna.Google Scholar
Remeš, F., Tomáš, R., Jindrák, V., Vaniš, V. & Setlík, M. 2013 Intraventricular and lumbar intrathecal administration of antibiotics in postneurosurgical patients with meningitis and/or ventriculitis in a serious clinical state. J. Neurosurg. 119, 1596–1602.Google Scholar
Riley, N. 2001 Steady streaming. Annu. Rev. Fluid Mech. 33, 43–65.Google Scholar
Sánchez, A. L., Martínez-Bazán, C., Gutiérrez-Montes, C., Criado-Hidalgo, E., Pawlak, G., Bradley, W., Haughton, V. & Lasheras, J. C. 2018 On the bulk motion of the cerebrospinal fluid in the spinal canal. J. Fluid Mech. 841, 203–227.Google Scholar
Sass, L. R., Khani, M., Natividad, G. C., Tubbs, S., Baledent, O. & Martin, B. A. 2017 A 3D subject-specific model of the spinal subarachnoid space with anatomically realistic ventral and dorsal spinal cord nerve rootlets. Fluids Barriers CNS 14 (36), 1–16.Google Scholar
Shafer, S. L., Eisenach, J. C., Hood, D. D. & Tong, C. 1998 Cerebrospinal fluid pharmacokinetics and pharmacodynamics of intrathecal neostigmine methylsulfate in humans. Anesthesiology 89, 1074–1088.Google Scholar
Shapiro, K., Marmarou, A. & Shulman, K. 1980 Characterization of clinical CSF dynamics and neural axis compliance using the pressure–volume index. Part I. The normal pressure–volume index. Ann. Neurol. 7 (6), 508–514.Google Scholar
Stockman, H. W. 2007 Effect of anatomical fine structure on the dispersion of solutes in the spinal subarachnoid space. J. Biomech. Engng 129 (5), 666–675.Google Scholar
Tangen, K., Leval, R., Mehta, A. I. & Linninger, A. A. 2017 Computational and in vitro experimental investigation of intrathecal drug distribution: parametric study of the effect of injection volume, cerebrospinal fluid pulsatility, and drug uptake. Anesth. Analg. 124, 1686–1696.Google Scholar
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Wallace, M. & Yaksh, T. L. 2012 Characteristics of distribution of morphine and metabolites in cerebrospinal fluid and plasma with chronic intrathecal morphine infusion in humans. Anesth. Analg. 115, 797–804.Google Scholar
Watson, E. J. 1983 Diffusion in oscillatory pipe flow. J. Fluid Mech. 133, 233–244.Google Scholar