Article contents
On the correlation between vortex breakdown bubble and planar helicity in Vogel–Escudier flow
Published online by Cambridge University Press: 06 February 2020
Abstract
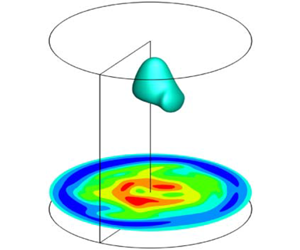
Bubble-type vortex breakdown in axial vortices is investigated numerically through a model problem of flow inside a cylinder with a top rotating lid, referred to as ‘Vogel–Escuider flow’. The parameters of the flow are Reynolds number ( $Re$), based on the rotation speed of the top plate, and aspect ratio (
$Re$), based on the rotation speed of the top plate, and aspect ratio ( $\unicode[STIX]{x1D6E4}$), which is the ratio of height to radius of the cylinder, depending on which the flow exhibits steady or unsteady breakdown bubble topologies. The flow is analysed for Reynolds number up to 5000 for
$\unicode[STIX]{x1D6E4}$), which is the ratio of height to radius of the cylinder, depending on which the flow exhibits steady or unsteady breakdown bubble topologies. The flow is analysed for Reynolds number up to 5000 for  $\unicode[STIX]{x1D6E4}=2.5$ using helicity density. In the absence of vortex breakdown, the helicity density does not change the sign in the bulk, while in the event of a breakdown, it changes the sign from positive to negative in the vicinity of the breakdown bubble. The three-dimensional flow is further represented as the sum of a two-dimensional velocity field in the
$\unicode[STIX]{x1D6E4}=2.5$ using helicity density. In the absence of vortex breakdown, the helicity density does not change the sign in the bulk, while in the event of a breakdown, it changes the sign from positive to negative in the vicinity of the breakdown bubble. The three-dimensional flow is further represented as the sum of a two-dimensional velocity field in the  $rz$ plane and an out-of-plane velocity vector based on the respective energies, referred to as two-dimensional three-component flow. Here
$rz$ plane and an out-of-plane velocity vector based on the respective energies, referred to as two-dimensional three-component flow. Here  $r$ is the radial coordinate,
$r$ is the radial coordinate,  $z$ is the axial coordinate and
$z$ is the axial coordinate and  $\unicode[STIX]{x1D703}$ is the azimuthal coordinate. Helicity density of the flow is then decomposed into planar helicity
$\unicode[STIX]{x1D703}$ is the azimuthal coordinate. Helicity density of the flow is then decomposed into planar helicity  $(h_{r,z})$ and out-of-plane helicity
$(h_{r,z})$ and out-of-plane helicity  $(h_{\unicode[STIX]{x1D703}})$. We show that a correlation exists between planar helicity and the vortex breakdown bubble. We also show that the topology of the breakdown bubbles is described by the planar helicity. Using only this planar helicity, the entire breakdown bubble is reconstructed for axisymmetric as well as non-axisymmetric flows.
$(h_{\unicode[STIX]{x1D703}})$. We show that a correlation exists between planar helicity and the vortex breakdown bubble. We also show that the topology of the breakdown bubbles is described by the planar helicity. Using only this planar helicity, the entire breakdown bubble is reconstructed for axisymmetric as well as non-axisymmetric flows.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 16
- Cited by


