On the contact region of a diffusion-limited evaporating drop: a local analysis

Abstract

Motivated by experiments showing that a sessile drop of volatile perfectly wetting liquid initially advances over the substrate, but then reverses, we formulate the problem describing the contact region at reversal. Assuming a separation of scales, so that the radial extent of this region is small compared with the instantaneous radius $a$ of the apparent contact line, we show that the time scale characterizing the contact region is small compared with that on which the bulk drop is evolving. As a result, the contact region is governed by a boundary-value problem, rather than an initial-value problem: the contact region has no memory, and all its properties are determined by conditions at the instant of reversal. We conclude that the apparent contact angle 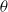$\theta $ is a function of the instantaneous drop radius $a$, as found in the experiments. We then non-dimensionalize the boundary-value problem, and find that its solution depends on one parameter 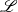$\mathscr{L}$, a dimensionless surface tension. According to this formulation, the apparent contact angle is well-defined: at the outer edge of the contact region, the film slope approaches a limit that is independent of the curvature of bulk drop. In this, it differs from the dynamic contact angle observed during spreading of non-volatile drops. Next, we analyse the boundary-value problem assuming 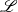$\mathscr{L}$ to be small. Though, for arbitrary 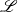$\mathscr{L}$, determining 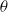$\theta $ requires solving the steady diffusion equation for the vapour, there is, for small 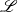$\mathscr{L}$, a further separation of scales within the contact region. As a result, 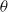$\theta $ is now determined by solving an ordinary differential equation. We predict that 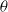$\theta $ varies as 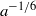${a}^{- 1/ 6} $, as found experimentally for small drops (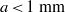$a\lt 1~\mathrm{mm} $). For these drops, predicted and measured angles agree to within 10–30 %. Because the discrepancy increases with $a$, but 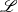$\mathscr{L}$ is a decreasing function of $a$, we infer that some process occurring outside the contact region is required to explain the observed behaviour of larger drops having 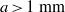$a\gt 1~\mathrm{mm} $.