1. Introduction
Anyone who has found themselves strolling along the beach on a pleasant day and idly attempted to skim a choice pebble across the incoming waves has perhaps developed an intuition as to what increases the chances of a good bounce. Some might conjecture it is the angle or speed of release, the shape of the pebble or the calmness of the sea – it is true that each of these can play an important role. However, perhaps less frequently considered is the air that is trapped between stone and water as it nears the surface, although the so-called air cushioning phenomenon is one that has fascinated researchers for many decades in the pages of Journal of Fluid Mechanics and further afield. A recent surge of interest in the interactions between impacts, air cushioning and bouncing has been excited in part by the work of Couder et al. (Reference Couder, Protiere, Fort and Boudaoud2005), whereby droplets heading towards a liquid bath may be driven to repeatedly bounce by vibrating the bath: a phenomenon that has inspired a slew of research into how fluid mechanics may provide a useful analogue for problems in quantum mechanics (Bush Reference Bush2015).
Characteristic in air cushioning dynamics is the interaction between comparatively large solid or liquid regions and the intervening air layer, which is typically significantly smaller in depth than in horizontal extent, so that it acts to lubricate the potential impact. Impact dynamics is characterized by a short time scale over which fluid surfaces may undergo rapid topological changes. This can be challenging to capture experimentally or numerically, so that a hybrid approach combining reduced models, direct numerical simulation (DNS) and experiments is often needed to gain physical insights.
Mathematical models for impact dynamics have a long history, tracing back to the pioneering work of von Kármán (Reference von Kármán1929) and Wagner (Reference Wagner1932), who were interested in predicting impact forces on alighting sea-planes. In particular, the latter's eponymous theory has long since been the standard in high-speed impact models, where effects such as gravity, capillarity, liquid viscosity and the surrounding air are considered negligible compared with liquid inertia to a first approximation. Despite these simplifications, Wagner theory holds up remarkably well both in solid and droplet impacts (Oliver Reference Oliver2007; Cimpeanu & Moore Reference Cimpeanu and Moore2018), particularly for predicting the growth of the effective wetted area. However, Wagner theory predicts an initially infinite liquid pressure at the keel of a solid impactor, whereas experimental data show an oscillating pressure profile (Howison, Ockendon & Wilson Reference Howison, Ockendon and Wilson1991). Moreover, for droplet impacts, the theory fails to describe the well-known bubble entrapment phenomenon (Thoroddsen et al. Reference Thoroddsen, Etoh, Takehara, Ootsuka and Hatsuki2005). Air cushioning is pivotal in both effects, which has driven extensive research to build air–liquid interactions into high-speed impacts (see e.g. Smith, Li & Wu Reference Smith, Li and Wu2003; Hicks & Purvis Reference Hicks and Purvis2013; Moore Reference Moore2021). The air layer acts to reduce the liquid pressure, while simultaneously deforming the air–liquid free surface. For a vertical impact, the free surface is pushed down below, and rises away from, the keel of the impactor, so that first contact (if it occurs) is away from the keel. Such air cushioning models have been successfully validated against both experiments and numerical simulations in the impact regime (see e.g. Hicks et al. Reference Hicks, Ermanyuk, Gavrilov and Purvis2012).
However, impact theory traditionally assumes a high-speed object that, even when affected by air cushioning, still makes contact with its target, leading to splashing. In the experiments of Couder et al. (Reference Couder, Protiere, Fort and Boudaoud2005), the droplets bounce rather than splash, which typically occurs due to lower impact speeds which allow for increased importance of effects such as capillarity, gravity and fluid viscosity. Galeano-Rios, Milewski & Vanden-Broeck (Reference Galeano-Rios, Milewski and Vanden-Broeck2017, Reference Galeano-Rios, Milewski and Vanden-Broeck2019) and Galeano-Rios et al. (Reference Galeano-Rios, Cimpeanu, Bauman, MacEwen, Milewski and Harris2021) develop an extension of inertial Wagner theory that can account for these effects through a quasi-potential formulation, in which a Helmholtz decomposition of the fluid velocity allows one to rewrite the governing fluid problem as a linearized Laplace problem for the velocity potential, with the additional physical effects incorporated into the free surface conditions. In these papers, the effect of the air layer is ignored and bouncing is mimicked by considering the impact of superhydrophobic spheres (i.e. with a contact angle of  $180^\circ$) on a liquid bath and imposing a so-called kinematic match (KM) for the liquid free surface that does not allow for the sphere to penetrate the liquid. The free surface is moved by matching its position and velocity to that of the sphere, while all contact is assumed to be tangential due to the hydrophobicity. Despite these simplifications, the KM model is shown to capture well bouncing behaviours such as the maximum penetration depth and the coefficient of restitution in the low-Weber-number regime, all at a significantly reduced cost to full DNS. Alventosa, Cimpeanu & Harris (Reference Alventosa, Cimpeanu and Harris2023) extend the KM model to droplet impacts and, in an effort to further reduce computational cost, perform the match at just the south pole of the droplet, again with promising results.
$180^\circ$) on a liquid bath and imposing a so-called kinematic match (KM) for the liquid free surface that does not allow for the sphere to penetrate the liquid. The free surface is moved by matching its position and velocity to that of the sphere, while all contact is assumed to be tangential due to the hydrophobicity. Despite these simplifications, the KM model is shown to capture well bouncing behaviours such as the maximum penetration depth and the coefficient of restitution in the low-Weber-number regime, all at a significantly reduced cost to full DNS. Alventosa, Cimpeanu & Harris (Reference Alventosa, Cimpeanu and Harris2023) extend the KM model to droplet impacts and, in an effort to further reduce computational cost, perform the match at just the south pole of the droplet, again with promising results.
Phillips & Milewski (Reference Phillips and Milewski2024) present a re-imagining of the KM model that directly couples the liquid flow to that in the intervening air layer, thereby capturing the full cushioning dynamics. They develop their model in such a way to cover both droplet impingement onto a liquid pool as well as impact by solid spheres, and compare their results with previous iterations of the KM model, DNS and experimental data. In so doing, Phillips & Milewski (Reference Phillips and Milewski2024) have made a significant step forwards in mathematical modelling of bouncing dynamics which, due to its substantial reduction in computing costs while capturing key physics, may play an important role in future developments in hydrodynamic-quantum analogues.
2. Overview
Phillips & Milewski (Reference Phillips and Milewski2024) present their model for droplet impact onto a deep bath of the same liquid, although the methodology is readily extended to solid–liquid problems. The model relies on a series of assumptions to simplify the Navier–Stokes equations in each of the three fluid regions. In the liquid bath, the main assumptions underlying the model are that the liquid flow is almost inviscid and that perturbations to the liquid free surface are small compared with the depth of the pool. They are therefore able to follow the KM model (Galeano-Rios et al. Reference Galeano-Rios, Milewski and Vanden-Broeck2017) by writing the fluid velocity using a Helmholtz decomposition, which reduces the bath problem to determining a potential that is harmonic in the lower half-space, with the viscous terms appearing in the kinematic and dynamic boundary conditions, where they appear as surface Laplacians of the potential and free surface perturbation, respectively. A similar velocity decomposition follows in the droplet, where the assumption of small free surface perturbations is here interpreted as small oscillations of the droplet around its steady spherical shape.
Formally, these reduced models are derived in the limit that capillarity is the dominant effect in free surface deformation, which is characteristic of low-speed impacts that lead to rebounding behaviour. The viscous terms enter at first order in the small Ohnesorge number  $Oh = \sqrt {We}/Re$, where
$Oh = \sqrt {We}/Re$, where  $We = \rho RU^2/\sigma$ and
$We = \rho RU^2/\sigma$ and  $Re = \rho RU/\mu$ are respectively the liquid Weber and Reynolds numbers based on the fluid density
$Re = \rho RU/\mu$ are respectively the liquid Weber and Reynolds numbers based on the fluid density  $\rho$ and dynamic viscosity
$\rho$ and dynamic viscosity  $\mu$, the air–liquid surface tension coefficient
$\mu$, the air–liquid surface tension coefficient  $\sigma$, and the droplet radius
$\sigma$, and the droplet radius  $R$ and impact speed
$R$ and impact speed  $U$. Since even low-speed impacts are characterized by high Reynolds numbers – for example, for a millimetric water droplet impacting at 10 cm s
$U$. Since even low-speed impacts are characterized by high Reynolds numbers – for example, for a millimetric water droplet impacting at 10 cm s $^{-1}$, we have
$^{-1}$, we have  $Re \approx 100$,
$Re \approx 100$,  $We \approx 0.14$ – this assumption is widely met.
$We \approx 0.14$ – this assumption is widely met.
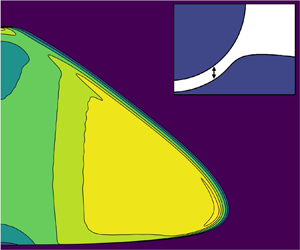
The key difference with the KM model and that of Phillips & Milewski (Reference Phillips and Milewski2024) is the presence of the air pressure in the dynamic boundary conditions. This pressure is determined by taking the lubrication limit in the air layer, so that the Reynolds equation must be solved in the evolving gap. Notably, the gap evolves both parallel and normal to the impact: the former is particularly important in modelling rebounds, where it is to be expected that the air cushioning region will contract as the impactor pulls away from the liquid bath. The flow problems are further coupled to an equation for the motion of the droplet centre of mass, which falls under gravity mediated by the pressure force exerted by the cushioning air layer. It is this pressure force that can induce bouncing.
The final piece of the modelling jigsaw employed by Phillips & Milewski (Reference Phillips and Milewski2024) is to exploit Dirichlet-to-Neumann maps for the Laplace problems in each liquid to rewrite the boundary conditions solely in terms of the potentials on the free surface rather than their derivatives. In this manner, Phillips & Milewski (Reference Phillips and Milewski2024) have elegantly reduced the full flow to determining the potentials on the free surface and corresponding Dirichlet-to-Neumann maps – which may be readily achieved using suitable eigenfunction decompositions depending on the geometry at hand – coupled to the lubrication equation in the air layer and the motion of the droplet centre of mass. The authors refer to the model as the lubrication-mediated (LM) model. The LM model is amenable to probing the conditions for bouncing, as well as the behaviours of the impactor and air cushioning layer in detail. When rebounds occur, the authors characterize them in terms of three key measures: the maximum penetration depth achieved by the impactor, the pressing time (defined as the time between the south pole of the impactor crossing the undisturbed waterline of the liquid bath on its up- and downwards trajectories) and third, the square of the coefficient of restitution, which is the ratio of the mechanical energies of the impactor at the start and end of the pressing time.
As alluded to above, it is in particular the potential for decomposing the variables that much of the computational expense and effort is reduced: rather than solving the full partial differential equations, whether Laplace's equation or Navier–Stokes, many impact scenarios may be reduced to solving ordinary differential equations for the coefficients of a suitable eigenfunction expansion. Phillips & Milewski (Reference Phillips and Milewski2024) illustrate this advantage by considering the example of an approximately millimetric solid hydrophobic sphere approaching a deep pool. This geometry admits axisymmetric solutions in cylindrical polar coordinates, with an associated eigenfunction expansion in terms of Bessel functions. Beyond geometric convenience, this example also allows for comparison with existing results of Galeano-Rios et al. (Reference Galeano-Rios, Cimpeanu, Bauman, MacEwen, Milewski and Harris2021), including experiments, DNS data and predictions of the KM model. The predictions of the LM model are shown to align well with this existing data, particularly in terms of the pressing time and restitution coefficient.
With this validation in hand, Phillips & Milewski (Reference Phillips and Milewski2024) conclude by using the LM model to reveal that the rebound has three distinct phases. The first phase is a rapid horizontal expansion of the air cushioning region as the impactor approaches the bath, typically lasting approximately a millisecond. The impactor feels a sharp pressure spike in this phase. In the second phase, the air layer gradually begins to contract as the impactor begins to rebound. This phase lasts approximately 10 ms and is characterized by a quasi-static pressure in the interior of the air cushioning layer, where the layer thickness is approximately 1  $\mathrm {\mu }$m. This pressure does the bulk of the work on the impactor in the rebound. The third phase is a rapid suction event as the impactor fully lifts off, lasting approximately 1 ms, and with an associated large, negative suction pressure on the south pole of the body. These behaviours are qualitatively consistent with existing studies on air cushioning (e.g. Tang et al. Reference Tang, Saha, Law and Sun2019).
$\mathrm {\mu }$m. This pressure does the bulk of the work on the impactor in the rebound. The third phase is a rapid suction event as the impactor fully lifts off, lasting approximately 1 ms, and with an associated large, negative suction pressure on the south pole of the body. These behaviours are qualitatively consistent with existing studies on air cushioning (e.g. Tang et al. Reference Tang, Saha, Law and Sun2019).
3. Future directions
It is this level of detail in the impact dynamics at a relatively cheap computational cost – of the order of hours on a personal laptop – that the LM model represents a step improvement in the field of impacts and promises to be a powerful tool in future research. The authors themselves note that the preliminary comparisons with other models presented in the study need to be expanded going forward, and it is a natural question to wonder in which particular areas the LM model excels as compared with other reduced models such as the KM model or full DNS. Understanding the flexibility and limitations of the toolkit at the modeller's disposal will prove a critical factor going forward.
Another potentially important avenue of extension will be to consider non-vertical rebounds, which are more closely aligned to walking droplets (Couder et al. Reference Couder, Protiere, Fort and Boudaoud2005) or applications to autonomous walking robots modelled on water striders that have been proposed for environmental exploration (Yang et al. Reference Yang, Liu, Yan, Wang, Zhang and Zhao2016). Oblique impact problems also break the axisymmetry of the impacting sphere or spherical droplet: given the general derivation of the LM model, it will be interesting to see it employed to fully three-dimensional problems, which always present a challenge for direct computations.
Perhaps a longer term goal might be to think about how the model parameters can be tuned or controlled to get the desired behaviour of the impactor. Is it readily predictable for what parameters the droplet may bounce once before being captured by the liquid bath? What happens if the two liquids are different or if the depth of the pool is reduced? As always with an exciting new mathematical model, the possibilities are varied and numerous: the future of impact dynamics is positively bouncing.




1. Introduction
Anyone who has found themselves strolling along the beach on a pleasant day and idly attempted to skim a choice pebble across the incoming waves has perhaps developed an intuition as to what increases the chances of a good bounce. Some might conjecture it is the angle or speed of release, the shape of the pebble or the calmness of the sea – it is true that each of these can play an important role. However, perhaps less frequently considered is the air that is trapped between stone and water as it nears the surface, although the so-called air cushioning phenomenon is one that has fascinated researchers for many decades in the pages of Journal of Fluid Mechanics and further afield. A recent surge of interest in the interactions between impacts, air cushioning and bouncing has been excited in part by the work of Couder et al. (Reference Couder, Protiere, Fort and Boudaoud2005), whereby droplets heading towards a liquid bath may be driven to repeatedly bounce by vibrating the bath: a phenomenon that has inspired a slew of research into how fluid mechanics may provide a useful analogue for problems in quantum mechanics (Bush Reference Bush2015).
Characteristic in air cushioning dynamics is the interaction between comparatively large solid or liquid regions and the intervening air layer, which is typically significantly smaller in depth than in horizontal extent, so that it acts to lubricate the potential impact. Impact dynamics is characterized by a short time scale over which fluid surfaces may undergo rapid topological changes. This can be challenging to capture experimentally or numerically, so that a hybrid approach combining reduced models, direct numerical simulation (DNS) and experiments is often needed to gain physical insights.
Mathematical models for impact dynamics have a long history, tracing back to the pioneering work of von Kármán (Reference von Kármán1929) and Wagner (Reference Wagner1932), who were interested in predicting impact forces on alighting sea-planes. In particular, the latter's eponymous theory has long since been the standard in high-speed impact models, where effects such as gravity, capillarity, liquid viscosity and the surrounding air are considered negligible compared with liquid inertia to a first approximation. Despite these simplifications, Wagner theory holds up remarkably well both in solid and droplet impacts (Oliver Reference Oliver2007; Cimpeanu & Moore Reference Cimpeanu and Moore2018), particularly for predicting the growth of the effective wetted area. However, Wagner theory predicts an initially infinite liquid pressure at the keel of a solid impactor, whereas experimental data show an oscillating pressure profile (Howison, Ockendon & Wilson Reference Howison, Ockendon and Wilson1991). Moreover, for droplet impacts, the theory fails to describe the well-known bubble entrapment phenomenon (Thoroddsen et al. Reference Thoroddsen, Etoh, Takehara, Ootsuka and Hatsuki2005). Air cushioning is pivotal in both effects, which has driven extensive research to build air–liquid interactions into high-speed impacts (see e.g. Smith, Li & Wu Reference Smith, Li and Wu2003; Hicks & Purvis Reference Hicks and Purvis2013; Moore Reference Moore2021). The air layer acts to reduce the liquid pressure, while simultaneously deforming the air–liquid free surface. For a vertical impact, the free surface is pushed down below, and rises away from, the keel of the impactor, so that first contact (if it occurs) is away from the keel. Such air cushioning models have been successfully validated against both experiments and numerical simulations in the impact regime (see e.g. Hicks et al. Reference Hicks, Ermanyuk, Gavrilov and Purvis2012).
However, impact theory traditionally assumes a high-speed object that, even when affected by air cushioning, still makes contact with its target, leading to splashing. In the experiments of Couder et al. (Reference Couder, Protiere, Fort and Boudaoud2005), the droplets bounce rather than splash, which typically occurs due to lower impact speeds which allow for increased importance of effects such as capillarity, gravity and fluid viscosity. Galeano-Rios, Milewski & Vanden-Broeck (Reference Galeano-Rios, Milewski and Vanden-Broeck2017, Reference Galeano-Rios, Milewski and Vanden-Broeck2019) and Galeano-Rios et al. (Reference Galeano-Rios, Cimpeanu, Bauman, MacEwen, Milewski and Harris2021) develop an extension of inertial Wagner theory that can account for these effects through a quasi-potential formulation, in which a Helmholtz decomposition of the fluid velocity allows one to rewrite the governing fluid problem as a linearized Laplace problem for the velocity potential, with the additional physical effects incorporated into the free surface conditions. In these papers, the effect of the air layer is ignored and bouncing is mimicked by considering the impact of superhydrophobic spheres (i.e. with a contact angle of $180^\circ$) on a liquid bath and imposing a so-called kinematic match (KM) for the liquid free surface that does not allow for the sphere to penetrate the liquid. The free surface is moved by matching its position and velocity to that of the sphere, while all contact is assumed to be tangential due to the hydrophobicity. Despite these simplifications, the KM model is shown to capture well bouncing behaviours such as the maximum penetration depth and the coefficient of restitution in the low-Weber-number regime, all at a significantly reduced cost to full DNS. Alventosa, Cimpeanu & Harris (Reference Alventosa, Cimpeanu and Harris2023) extend the KM model to droplet impacts and, in an effort to further reduce computational cost, perform the match at just the south pole of the droplet, again with promising results.
$180^\circ$) on a liquid bath and imposing a so-called kinematic match (KM) for the liquid free surface that does not allow for the sphere to penetrate the liquid. The free surface is moved by matching its position and velocity to that of the sphere, while all contact is assumed to be tangential due to the hydrophobicity. Despite these simplifications, the KM model is shown to capture well bouncing behaviours such as the maximum penetration depth and the coefficient of restitution in the low-Weber-number regime, all at a significantly reduced cost to full DNS. Alventosa, Cimpeanu & Harris (Reference Alventosa, Cimpeanu and Harris2023) extend the KM model to droplet impacts and, in an effort to further reduce computational cost, perform the match at just the south pole of the droplet, again with promising results.
Phillips & Milewski (Reference Phillips and Milewski2024) present a re-imagining of the KM model that directly couples the liquid flow to that in the intervening air layer, thereby capturing the full cushioning dynamics. They develop their model in such a way to cover both droplet impingement onto a liquid pool as well as impact by solid spheres, and compare their results with previous iterations of the KM model, DNS and experimental data. In so doing, Phillips & Milewski (Reference Phillips and Milewski2024) have made a significant step forwards in mathematical modelling of bouncing dynamics which, due to its substantial reduction in computing costs while capturing key physics, may play an important role in future developments in hydrodynamic-quantum analogues.
2. Overview
Phillips & Milewski (Reference Phillips and Milewski2024) present their model for droplet impact onto a deep bath of the same liquid, although the methodology is readily extended to solid–liquid problems. The model relies on a series of assumptions to simplify the Navier–Stokes equations in each of the three fluid regions. In the liquid bath, the main assumptions underlying the model are that the liquid flow is almost inviscid and that perturbations to the liquid free surface are small compared with the depth of the pool. They are therefore able to follow the KM model (Galeano-Rios et al. Reference Galeano-Rios, Milewski and Vanden-Broeck2017) by writing the fluid velocity using a Helmholtz decomposition, which reduces the bath problem to determining a potential that is harmonic in the lower half-space, with the viscous terms appearing in the kinematic and dynamic boundary conditions, where they appear as surface Laplacians of the potential and free surface perturbation, respectively. A similar velocity decomposition follows in the droplet, where the assumption of small free surface perturbations is here interpreted as small oscillations of the droplet around its steady spherical shape.
Formally, these reduced models are derived in the limit that capillarity is the dominant effect in free surface deformation, which is characteristic of low-speed impacts that lead to rebounding behaviour. The viscous terms enter at first order in the small Ohnesorge number $Oh = \sqrt {We}/Re$, where
$Oh = \sqrt {We}/Re$, where  $We = \rho RU^2/\sigma$ and
$We = \rho RU^2/\sigma$ and  $Re = \rho RU/\mu$ are respectively the liquid Weber and Reynolds numbers based on the fluid density
$Re = \rho RU/\mu$ are respectively the liquid Weber and Reynolds numbers based on the fluid density  $\rho$ and dynamic viscosity
$\rho$ and dynamic viscosity  $\mu$, the air–liquid surface tension coefficient
$\mu$, the air–liquid surface tension coefficient  $\sigma$, and the droplet radius
$\sigma$, and the droplet radius  $R$ and impact speed
$R$ and impact speed  $U$. Since even low-speed impacts are characterized by high Reynolds numbers – for example, for a millimetric water droplet impacting at 10 cm s
$U$. Since even low-speed impacts are characterized by high Reynolds numbers – for example, for a millimetric water droplet impacting at 10 cm s $^{-1}$, we have
$^{-1}$, we have  $Re \approx 100$,
$Re \approx 100$,  $We \approx 0.14$ – this assumption is widely met.
$We \approx 0.14$ – this assumption is widely met.
The key difference with the KM model and that of Phillips & Milewski (Reference Phillips and Milewski2024) is the presence of the air pressure in the dynamic boundary conditions. This pressure is determined by taking the lubrication limit in the air layer, so that the Reynolds equation must be solved in the evolving gap. Notably, the gap evolves both parallel and normal to the impact: the former is particularly important in modelling rebounds, where it is to be expected that the air cushioning region will contract as the impactor pulls away from the liquid bath. The flow problems are further coupled to an equation for the motion of the droplet centre of mass, which falls under gravity mediated by the pressure force exerted by the cushioning air layer. It is this pressure force that can induce bouncing.
The final piece of the modelling jigsaw employed by Phillips & Milewski (Reference Phillips and Milewski2024) is to exploit Dirichlet-to-Neumann maps for the Laplace problems in each liquid to rewrite the boundary conditions solely in terms of the potentials on the free surface rather than their derivatives. In this manner, Phillips & Milewski (Reference Phillips and Milewski2024) have elegantly reduced the full flow to determining the potentials on the free surface and corresponding Dirichlet-to-Neumann maps – which may be readily achieved using suitable eigenfunction decompositions depending on the geometry at hand – coupled to the lubrication equation in the air layer and the motion of the droplet centre of mass. The authors refer to the model as the lubrication-mediated (LM) model. The LM model is amenable to probing the conditions for bouncing, as well as the behaviours of the impactor and air cushioning layer in detail. When rebounds occur, the authors characterize them in terms of three key measures: the maximum penetration depth achieved by the impactor, the pressing time (defined as the time between the south pole of the impactor crossing the undisturbed waterline of the liquid bath on its up- and downwards trajectories) and third, the square of the coefficient of restitution, which is the ratio of the mechanical energies of the impactor at the start and end of the pressing time.
As alluded to above, it is in particular the potential for decomposing the variables that much of the computational expense and effort is reduced: rather than solving the full partial differential equations, whether Laplace's equation or Navier–Stokes, many impact scenarios may be reduced to solving ordinary differential equations for the coefficients of a suitable eigenfunction expansion. Phillips & Milewski (Reference Phillips and Milewski2024) illustrate this advantage by considering the example of an approximately millimetric solid hydrophobic sphere approaching a deep pool. This geometry admits axisymmetric solutions in cylindrical polar coordinates, with an associated eigenfunction expansion in terms of Bessel functions. Beyond geometric convenience, this example also allows for comparison with existing results of Galeano-Rios et al. (Reference Galeano-Rios, Cimpeanu, Bauman, MacEwen, Milewski and Harris2021), including experiments, DNS data and predictions of the KM model. The predictions of the LM model are shown to align well with this existing data, particularly in terms of the pressing time and restitution coefficient.
With this validation in hand, Phillips & Milewski (Reference Phillips and Milewski2024) conclude by using the LM model to reveal that the rebound has three distinct phases. The first phase is a rapid horizontal expansion of the air cushioning region as the impactor approaches the bath, typically lasting approximately a millisecond. The impactor feels a sharp pressure spike in this phase. In the second phase, the air layer gradually begins to contract as the impactor begins to rebound. This phase lasts approximately 10 ms and is characterized by a quasi-static pressure in the interior of the air cushioning layer, where the layer thickness is approximately 1 $\mathrm {\mu }$m. This pressure does the bulk of the work on the impactor in the rebound. The third phase is a rapid suction event as the impactor fully lifts off, lasting approximately 1 ms, and with an associated large, negative suction pressure on the south pole of the body. These behaviours are qualitatively consistent with existing studies on air cushioning (e.g. Tang et al. Reference Tang, Saha, Law and Sun2019).
$\mathrm {\mu }$m. This pressure does the bulk of the work on the impactor in the rebound. The third phase is a rapid suction event as the impactor fully lifts off, lasting approximately 1 ms, and with an associated large, negative suction pressure on the south pole of the body. These behaviours are qualitatively consistent with existing studies on air cushioning (e.g. Tang et al. Reference Tang, Saha, Law and Sun2019).
3. Future directions
It is this level of detail in the impact dynamics at a relatively cheap computational cost – of the order of hours on a personal laptop – that the LM model represents a step improvement in the field of impacts and promises to be a powerful tool in future research. The authors themselves note that the preliminary comparisons with other models presented in the study need to be expanded going forward, and it is a natural question to wonder in which particular areas the LM model excels as compared with other reduced models such as the KM model or full DNS. Understanding the flexibility and limitations of the toolkit at the modeller's disposal will prove a critical factor going forward.
Another potentially important avenue of extension will be to consider non-vertical rebounds, which are more closely aligned to walking droplets (Couder et al. Reference Couder, Protiere, Fort and Boudaoud2005) or applications to autonomous walking robots modelled on water striders that have been proposed for environmental exploration (Yang et al. Reference Yang, Liu, Yan, Wang, Zhang and Zhao2016). Oblique impact problems also break the axisymmetry of the impacting sphere or spherical droplet: given the general derivation of the LM model, it will be interesting to see it employed to fully three-dimensional problems, which always present a challenge for direct computations.
Perhaps a longer term goal might be to think about how the model parameters can be tuned or controlled to get the desired behaviour of the impactor. Is it readily predictable for what parameters the droplet may bounce once before being captured by the liquid bath? What happens if the two liquids are different or if the depth of the pool is reduced? As always with an exciting new mathematical model, the possibilities are varied and numerous: the future of impact dynamics is positively bouncing.
Acknowledgements
I would like to acknowledge helpful feedback from Dr A. Wray and Dr R. Cimpeanu on drafts of this article.
Declaration of interests
The author reports no conflict of interests.