On the absence of a secondary vortex street in three-dimensional and turbulent cylinder wakes

Abstract

Bluff-body wakes generally become three-dimensional (3-D) and then turbulent when the Reynolds number exceeds a few hundred. Other than an alternate shedding of the spanwise vortices behind the body and a gradual decay and annihilation of the vortices with distance downstream, whether a secondary vortex street would develop in the relatively far wake has been a long-standing argument in the literature. This argument is addressed in the present study. Specifically, direct numerical simulations and transient growth analysis are performed to examine the two-dimensional and 3-D wakes of different bluff bodies, including circular cylinder, square cylinder, diamond cylinder and rectangular cylinders with different cross-sectional aspect ratios. We found that a secondary vortex street is absent for most 3-D and turbulent wakes. The root cause is the weakening of spanwise vortices by 3-D wake instability modes and streamwise circulation/vorticity. The weakened spanwise vortices induce reduced mean shear in the intermediate wake, which then induces much smaller perturbation energy growth that is below the threshold for the emergence of a secondary vortex street. This finding suggests that the 3-D and turbulence characteristics, and the momentum, mass and heat transport in the relatively far wake of bluff bodies, would not be influenced by extra anisotropy or inhomogeneity caused by a secondary vortex street.

1. Introduction

Vortex shedding is a defining feature of the wake of cylindrical bluff bodies – e.g. mountainous island (figure 1), tall building, heat exchange tube, subsea cable and riser. The evolution and propagation of the vortices in the wake is an important topic of interest because the vortices affect strongly the strength and spatiotemporal distribution of the turbulence characteristics (Batchelor 1953; Hussain & Hayakawa 1987; Chen et al. 2016,  2018; Jiang et al. 2022) and the momentum, mass and heat transport in the wake (Antonia et al. 1987; Matsumura & Antonia 1993; Chen et al. 2016). In particular, the influence of the spanwise vortices extends well beyond the near-wake region (Antonia et al. 1987; Hussain & Hayakawa 1987; Matsumura & Antonia 1993; Chen et al. 2016,  2018; Jiang et al. 2022), which calls for an understanding of the downstream evolution of the vortex pattern.

Figure 1. Primary (Kármán) vortex street in the wake of Jan Mayen Island, visualised by a cloud layer. The wind is from left to right, and the measured area is 365 km by 158 km. Image credit: NASA/GSFC/LaRC/JPL, MISR Team.

The vortex patterns in laminar bluff-body wakes have been well studied in the literature. For various bodies, such as a circular cylinder (Taneda 1959; Cimbala, Nagib & Roshko 1988; Kumar & Mittal 2012), rectangular cylinder (Ju & Jiang 2022), triangular cylinder (Kim 2019) and rotated square cylinder (Jiang 2021a), a common phenomenon is that the primary (Kármán) vortex street may transition to a two-layered pattern in the intermediate wake, followed by a second transition to a secondary vortex street in the relatively far wake (figure 2a). In contrast to the time-periodic evolution of the primary vortices, the secondary vortices have irregular spatiotemporal distributions, increased sizes and reduced frequencies (Taneda 1959; Cimbala et al. 1988; Kumar & Mittal 2012). The transition to the two-layered and secondary vortex streets may also alter the hydrodynamic forces on the body and the three-dimensional (3-D) flow structures in the wake (Ju & Jiang 2024).

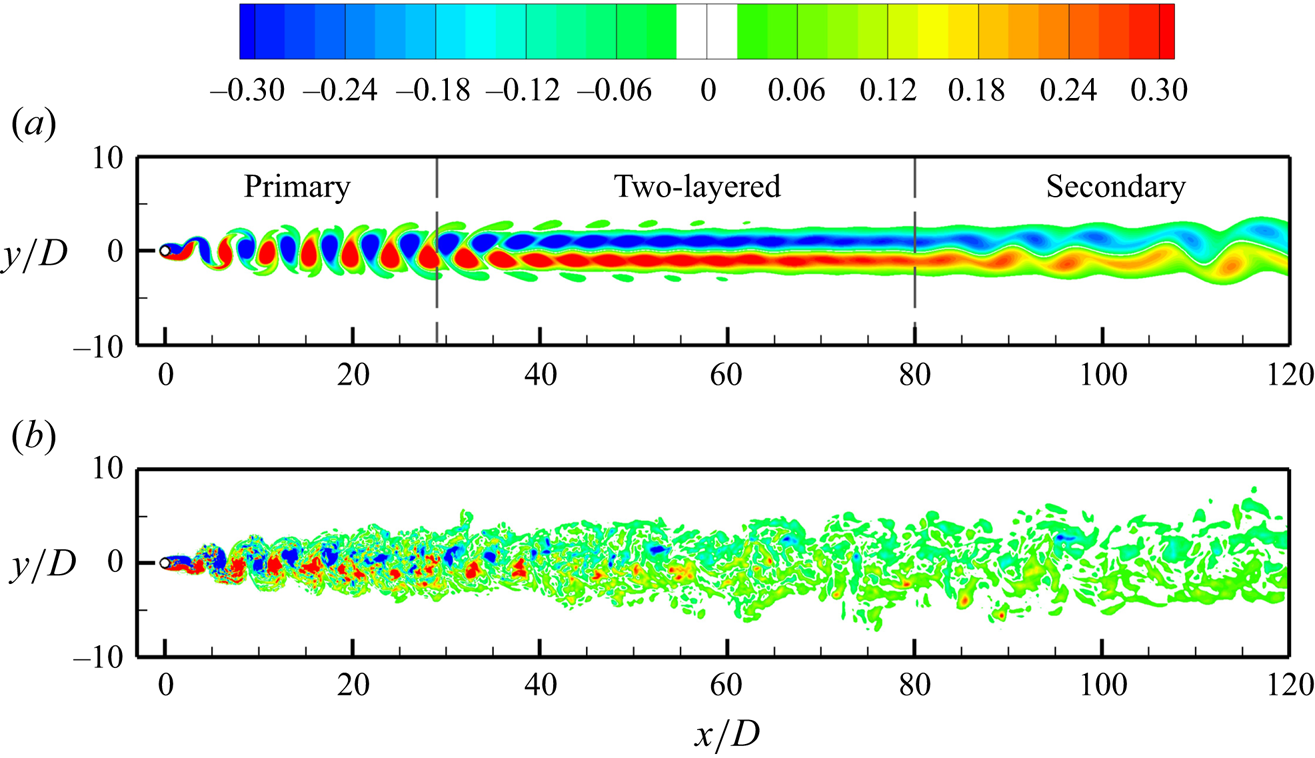
Figure 2. Instantaneous spanwise vorticity field in the wake of a circular cylinder: (a) two-dimensional laminar wake at $\textit {Re} = 200$, and (b) span-averaged three-dimensional turbulent wake at $\textit {Re} = 1000$. The flow is from left to right past the cylinder on the left.

Bluff-body wakes generally become 3-D and then turbulent when the Reynolds number $\textit {Re}$ ($= UD/\nu$), defined based on the free-stream velocity ($U$), length scale of the cylinder perpendicular to the free stream ($D$) and kinematic viscosity of the fluid ($\nu$), exceeds a few hundred. Bluff-body wakes in practice mostly sit in the turbulent regime. For 3-D and turbulent wakes, however, there has been no solid evidence in the literature justifying either the existence or absence of the secondary vortex street.

1. (i) Several early experimental studies reported groups, bursts or bulges of large-scale spanwise vortical structures in the far wake of a circular cylinder – e.g. by Grant (1958) at $\textit {Re} = 1300$ and $x/D = 533$, by Townsend (1979) at $\textit {Re} \sim 8000$ and $x/D = 170$, by Antonia et al. (1987) at $\textit {Re} \sim 1200$ and $x/D = 420$, and by Cimbala et al. (1988) at $\textit {Re} = 2200$ and $x/D \sim 250$ – but Cimbala et al. (1988) also stated that they could not find a well-organised, easily recognisable secondary vortex street in the turbulent regime. Without clear flow visualisation or theoretical justification, one cannot conclude if the groups, bursts or bulges were indeed secondary vortex streets, or if they were generated by e.g. a common experimental artefact called oblique shedding (Williamson 1989) and the consequent far-wake 3-D honeycomb pattern elucidated by Williamson & Prasad (1993) more recently, the residual smoke/dye pattern of the upstream flow (Cimbala et al. 1988), or a group of small-scale turbulent structures, to name a few.

2. (ii) To eliminate the influence of oblique shedding and residual smoke/dye patterns, 3-D direct numerical simulations (DNS) may be employed. However, our 3-D DNS results of flow past a circular cylinder at $\textit {Re} = 1000$ (figure 2b) show that organised large-scale spanwise vortical structures can hardly be identified beyond $x/D \sim 20\unicode{x2013}40$.

3. (iii) Because it is difficult to identify organised large-scale spanwise vortical structures in a turbulent wake through visualisation, phase average was commonly used by experimental and numerical studies to reveal the Kármán-type vortices (e.g. Antonia et al. 1987; Matsumura & Antonia 1993; Chen et al. 2016; Jiang et al. 2022). The phase average was performed following a distinct primary vortex shedding frequency. However, after annihilation of the primary vortices in the intermediate wake (e.g. at $x/D \sim 40\unicode{x2013}75$ for a turbulent circular cylinder wake with $\textit {Re} > 500$), there is no longer a distinct frequency peak (Roshko 1954; Cimbala et al. 1988; Browne, Antonia & Shah 1989; Jiang et al. 2022), such that the phase-averaging technique cannot be used to identify the irregular secondary vortices.

4. (iv) Tang et al. (2018) used the proper orthogonal decomposition (POD) method to decompose the instantaneous vorticity field at $\textit {Re} = 3460$ into several POD modes, and suggested co-existence of the POD patterns resembling the primary and secondary vortex streets in the intermediate wake (over their view window $22 < x/D < 47$ and $-3 < y/D < 3$). However, the POD modes corresponding to the secondary vortex street accounted for only 2.4 % of the total enstrophy in their intermediate-wake view window (Tang et al. 2018), and we believe that such a small component is unlikely to have a global effect in the intermediate wake. Instead, the POD modes may imply existence of perturbation for the secondary vortex street, but it remains a question whether the perturbation would grow strong enough further downstream to produce the secondary vortices.

In light of the earlier studies, the present study aims to address the long-standing argument on the existence/absence of the secondary vortex street in 3-D and turbulent wakes. Previous studies have shown that it is difficult to justify the existence/absence of the secondary vortex street through flow visualisation, phase averaging or POD techniques. Therefore, the present study will tackle this problem through new perspectives.

2. Numerical model

2.1. Direct numerical simulations

For the present DNS, the governing equations were the continuity and incompressible Navier–Stokes equations:

(2.1)$$\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u}=0, \end{gather}$$

(2.2)$$\begin{gather}\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u}={-}\boldsymbol{\nabla}p+\nu\,\nabla^{2}\boldsymbol{u}, \end{gather}$$

where $\boldsymbol {u}(\boldsymbol {x}, t) = (u_x, u_y, u_z)(x, y, z, t)$ is the velocity field in Cartesian coordinates, $p(\boldsymbol {x}, t)$ is kinematic pressure defined as pressure divided by fluid density, $t$ is time, and $\nu$ is kinematic viscosity.

Equations (2.1) and (2.2) were solved by the open-source code Nektar++ (Cantwell et al. 2015) through the so-called quasi-3-D approach, where the flow in the $x$–$y$ plane was solved by a high-order spectral/hp element method (Karniadakis & Sherwin 2005), while that along the spanwise direction was expressed by a Fourier expansion (Karniadakis 1990). The same numerical approach was used by Jiang et al. (2022) and Jiang & Cheng (2021) for the simulation of flow past a circular cylinder over $\textit {Re} = 400\unicode{x2013}3900$, and more details on the numerical set-up can be found therein.

2.2. Numerical cases

A series of numerical cases was performed in this study to examine the effects of wake three-dimensionality, chaos and turbulence on the existence/absence of the secondary vortex street. For a circular cylinder, the wake transitions to three-dimensionality at $\textit {Re} \sim 180\unicode{x2013}205$, depending on the experimental set-up and end condition employed (Miller & Williamson 1994; Williamson 1996).

1. (i) The two-dimensional (2-D) DNS were performed over $\textit {Re} = 100\unicode{x2013}200$ to examine the 2-D laminar regime (figures 2a and 3a).

2. (ii) The 3-D DNS were performed at $\textit {Re} = 200$ and spanwise domain length $L_{z}/D = 3.5$ (comparable to the spanwise period of the mode A wake structure; Williamson 1996) to force development of one spanwise period of perfectly time-periodic mode A structure in the wake, such that the wake is 3-D but not chaotic or turbulent (figure 3b).

3. (iii) The 3-D DNS were also performed at $\textit {Re} = 200$ and $L_{z}/D = 12$, which accommodates at least three spanwise periods of the mode A structure and thus allows development of a 3-D chaotic wake (figure 3c).

4. (iv) More 3-D DNS were performed at $\textit {Re} = 1000$ and $L_{z}/D = 6$, where the wake is 3-D, chaotic and turbulent (figure 3d).

In figure 3, the spanwise vorticity ($\omega _{z}$) and streamwise vorticity ($\omega _{x}$) are defined in a non-dimensional form:

(2.3)$$\begin{gather} \omega_{z}=\left(\frac{\partial{u_y}}{\partial{x}}-\frac{\partial{u_x}}{\partial{y}}\right)\frac{D}{U}, \end{gather}$$

(2.4)$$\begin{gather}\omega_{x}=\left(\frac{\partial{u_z}}{\partial{y}}-\frac{\partial{u_y}}{\partial{z}}\right)\frac{D}{U}. \end{gather}$$

Figure 3. Instantaneous spanwise vorticity field in the wake of a circular cylinder: (a) 2-D laminar wake at $\textit {Re} = 200$; (b) 3-D time-periodic wake at $\textit {Re} = 200$ with $L_{z}/D = 3.5$; (c) 3-D chaotic wake at $\textit {Re} = 200$ with $L_{z}/D = 12$; and (d) 3-D turbulent wake at $\textit {Re} = 1000$ with $L_{z}/D = 6$. The translucent iso-surfaces represent spanwise vortices ($\omega _{z} = \pm 0.5$ for $\textit {Re} = 200$, and $\omega _{z} = \pm 2$ for $\textit {Re} = 1000$), while the opaque iso-surfaces represent streamwise vortices ($\omega _{x} =\pm 0.3$ for $\textit {Re} = 200$, and $\omega _{x} = \pm 3$ for $\textit {Re} = 1000$). Dark grey and light yellow denote positive and negative vorticity values, respectively. The flow is from left to right past the cylinder on the left.

2.3. Computational domain and mesh

The present DNS adopted a rectangular computational domain in the $x$–$y$ plane. The centre of the cylinder was located at the origin. The domain size was $-30\,{\leqslant}\,x/D\,{\leqslant}\,120$ in the streamwise direction, and $-30 \leqslant y/D \leqslant 30$ in the transverse direction. The boundary conditions for the velocity included a uniform streamwise velocity $U$ for the inlet ($x/D = -30$) and transverse ($y/D = \pm 30$) boundaries, a Neumann condition for the outlet ($x/D = 120$), and a no-slip condition for the cylinder surface. The boundary conditions for the pressure included a reference of zero for the outlet, and a high-order Neumann condition (Karniadakis, Israeli & Orszag 1991) for other boundaries. For the 3-D simulations, periodic boundary conditions were employed at the two boundaries perpendicular to the cylinder axis.

The present macro-element mesh was identical to that used by Jiang et al. (2022) for $\textit {Re} = 1000$. Although Jiang et al. (2022) demonstrated through a detailed mesh convergence study that a quadrilateral expansion of fourth-order Lagrange polynomials (denoted $N_p = 4$) for each macro element was adequate, a finer resolution of $N_p = 5$ was used in the present study. For $\textit {Re} = 1000$, the 3-D mesh was constructed by using 128 Fourier planes over the spanwise domain length $L_z/D = 6$, which was the same as that used by Jiang et al. (2022). For $\textit {Re} = 300$, 128 Fourier planes were used over $L_z/D = 12$, which was finer than that used by Jiang et al. (2016) for $\textit {Re} = 300$.

2.4. Transient growth analysis

In addition to the DNS, transient growth analysis was used in §§ 3.3 and 3.4 to determine the optimal/maximum growth of perturbation energy that is achievable in a given shear flow. As demonstrated in the laminar wakes of a circular cylinder over $\textit {Re} = 100\unicode{x2013}200$, although the secondary vortex street develops at very different streamwise locations for different $\textit {Re}$, it consistently develops at the streamwise locations where the maximum energy growth $G(\tau )$ grows to $10^5$–$10^7$ (Jiang 2021b), such that the degree of energy growth may serve as an indicator for the development of the secondary vortex street.

For a given time interval $\tau$ for the time evolution of perturbation, the transient growth analysis determines an optimal initial perturbation field (at $t^* = 0$) that leads to the maximum energy growth $G(\tau )$ at $t^* = \tau$, where $G(\tau )$ is calculated as

(2.5)\begin{equation} G(\tau)=\max\frac{E(t^*=\tau)}{E(t^*=0)}, \end{equation}

and the perturbation energy is calculated as

(2.6)\begin{equation} E=\tfrac{1}{2}\int_\varOmega(u_x'^2+u_y'^2)\,\mathrm{d}\varOmega, \end{equation}

where $u' = (u_x', u_y')$ is the perturbation velocity, and $\varOmega$ is the area of the computational domain. More details on the transient growth analysis can be found in Blackburn, Barkley & Sherwin (2008) and Jiang (2021b). For the 3-D turbulent cases, span-averaged flows were used for the transient growth analysis, such that the numerical set-up followed directly that used by Jiang (2021b) for the analysis of the 2-D laminar flows.

3. Results and discussion

3.1. Characteristics of the mean shear in a circular cylinder wake

Previous studies on the laminar wake of a circular cylinder have shown that the physical mechanism for the development of the secondary vortices is the hydrodynamic/convective instability of the mean wake flow (Cimbala et al. 1988; Williamson & Prasad 1993; Kumar & Mittal 2012), in particular over the region of the two-layered vortex street where large velocity deficit near the wake centreline induces large shear rates in the wake, which results in massive transient growth (amplification) of the perturbation energy to a point where flapping/waviness of the two shear layers induces individual secondary vortices (Jiang 2021b).

Because the secondary vortex street is fundamentally induced by large shear rates in the wake (Jiang 2021b), the shear rates for different cases are examined. Figure 4(a) illustrates the mean streamwise velocity ($\overline{u_x}$) profiles sampled at the intermediate wake of $x/D = 40$. To maximise the statistical accuracy, the mean quantities are averaged over time (of at least 200 vortex shedding periods), over cylinder span, and between the two sides of the wake centreline ($y = 0$). To approximately compare the level of mean shear of different cases, several metrics may be used, which include:

1. (i) the velocity deficit at the wake centreline $U_0$, defined as the difference between the free-stream velocity $U$ and the mean streamwise velocity at the wake centreline (illustrated in figure 4a)

2. (ii) the wake half-width $L$, defined as the transverse distance between the wake centreline and the location where the velocity deficit is $U_0/2$ (illustrated in figure 4a), as this definition is commonly used for quantifying the intermediate- and far-wake characteristics of a cylinder (e.g. Matsumura & Antonia 1993; Tang et al. 2016)

3. (iii) the maximum shear rate $(\partial \overline{u_x}/\partial y)_{max}$ along the streamwise velocity profile.

Figure 4. Characteristics of the mean shear in the wake: (a) time- and span-averaged streamwise velocity profiles sampled at $x/D = 40$; (b) streamwise variation of the velocity deficit at the wake centreline; (c) streamwise variation of the wake half-width; and (d) streamwise variation of the maximum shear rate.

Figures 4(b–d) quantify the streamwise variation of $U_0$, $L$ and $(\partial \overline{u_x}/\partial y)_{max}$ for different cases. At $\textit {Re} = 200$, the 2-D wake displays significantly larger $U_0$, smaller $L$, and significantly larger $(\partial \overline{u_x}/\partial y)_{max}$ than the 3-D wake with $L_{z}/D = 3.5$, which suggests that the mean shear in the wake is significantly reduced as the wake transitions from two to three dimensions, even before chaos and turbulence develop. To further explore the effect of this significant reduction in the mean shear, we perform an addition simulation with $\textit {Re} = 200$ and $L_{z}/D = 3.5$, but the wake length is significantly expanded to 400$D$. For this case, a regular two-layered pattern is observed up to the outflow boundary, which serves as strong evidence for the absence of a secondary vortex street.

For the cases with $\textit {Re} \geqslant 200$ and $L_{z}/D$ at least three times the spanwise period of the wake mode (Jiang, Cheng & An 2017), the wake becomes spatiotemporally chaotic (figures 3c,d), such that the far-wake pattern can hardly be determined by flow visualisation. Nevertheless, the similar levels of mean shear for $\textit {Re} = 200$ with $L_{z}/D = 3.5$ and 12 (figure 4) suggests that in reality (i.e. for a long span), a secondary vortex street is also absent at $\textit {Re} = 200$. The main reason for the absence of a secondary vortex street is the development of three-dimensionality, whereas the effect of spatiotemporal chaos is minor. With the increase in $\textit {Re}$ from 200 to 300 and 1000 (and beyond), the mean shear continues to decrease (figure 4), which suggests increasing unlikelihood of development of a secondary vortex street.

3.2. Reason for the decrease in the mean shear in 3-D wakes

For the 2-D wake of $\textit {Re} = 200$, the strong mean shear in the intermediate wake (peaked at $x/D \sim 40$; figure 4) is induced by the development of the two-layered vortex pattern (figure 2a) and the associated generation of a ‘calm region’ near the wake centreline with large velocity deficit (Durgin & Karlsson 1971; Jiang & Cheng 2019). Therefore, the significant reduction in the mean shear at the wake transition to three dimensions is attributed to weakened spanwise vortices constituting the two-layered pattern.

For a circular cylinder, the first 3-D wake instability mode is mode A (figure 3b), which is induced by an elliptic instability of the spanwise vortices and formation of streamwise vortex pairs through Biot–Savart induction (Williamson 1996). When the spanwise vortices are distorted (figure 3b versus figure 3a) by 3-D wake instability modes, their strength is reduced. In figure 5, the strength of the spanwise vortices is quantified by the spanwise circulation ($\varGamma _z$) within each vortex, where $\varGamma _z$ is calculated as

(3.1)\begin{equation} \varGamma_z=\int_{\varOmega}{\omega_z}\,\mathrm{d}\varOmega, \end{equation}

where $\varOmega$ represents the area of the vortex, which is determined as the area within which the vorticity is larger than one-third of the peak vorticity. The streamwise location of the vortex is determined at the centroid of a vortex

(3.2)\begin{equation} x_c=\frac{\displaystyle\int\nolimits_{\varOmega}{\omega_z}x\,\mathrm{d}\varOmega} {\displaystyle\int\nolimits_{\varOmega}{\omega_z}\,\mathrm{d}\varOmega}. \end{equation}

As shown in figure 5, at $\textit {Re} = 200$, the distorted spanwise vortices in the 3-D flows are noticeably weaker than the parallel spanwise vortices in the 2-D regime, which induce reduced mean shear (figure 4) and eventually absence of a secondary vortex street.

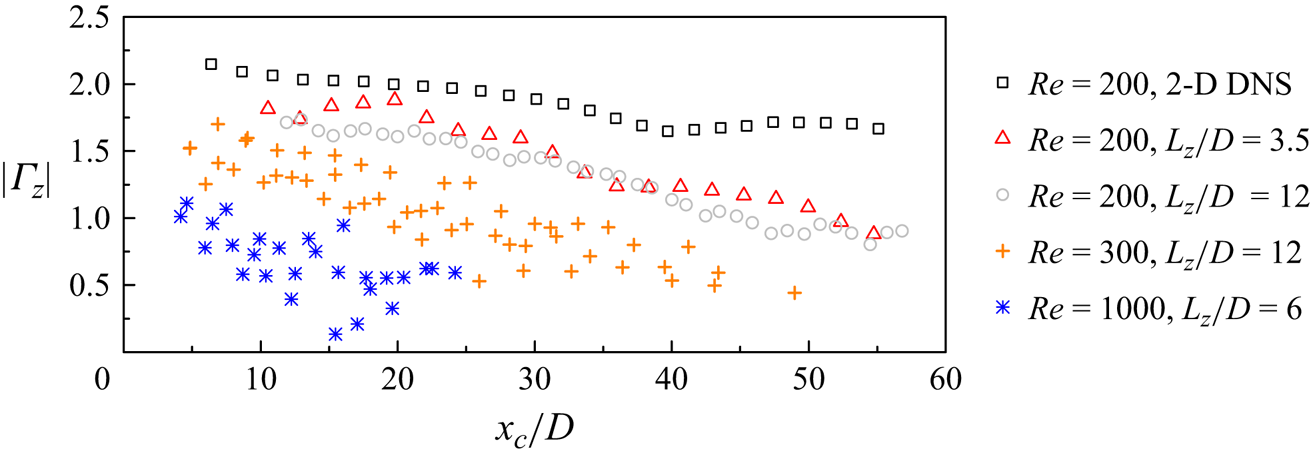
Figure 5. Streamwise variation of the circulation of spanwise vortices.

With the increase in $\textit {Re}$ from 200 to 300 and 1000 (and beyond), the strength of the spanwise vortices continues to decrease (figure 5). This is because when the level of flow three-dimensionality increases with increasing $\textit {Re}$ (Jiang 2020), the increase in the streamwise circulation/vorticity occurs at the expense of the spanwise circulation/vorticity (Norberg 2003; Menon, Kumar & Mittal 2022). Consequently, a secondary vortex street becomes increasingly unlikely to occur.

The above analysis suggests that flow three-dimensionality is not the root cause for the absence of a secondary vortex street. The root cause is the weakening of spanwise vortices by 3-D wake instability modes and streamwise circulation/vorticity. Therefore, a secondary vortex street may be observed in 3-D flows under rare scenarios, where the spanwise vortices are hardly affected by flow three-dimensionality. Specifically: (i) the 3-D wake instability mode does not distort the spanwise vortices (e.g. for hyperbolic wake instability modes such as mode B; Williamson 1996); and (ii) the streamwise circulation/vorticity is minor (e.g. for $\textit {Re}$ close to the onset of three-dimensionality). An example is the 3-D wake of a rectangular cylinder with cross-sectional aspect ratio $AR$ (the ratio between the streamwise and transverse lengths of the body) 0.125 and $\textit {Re} = 200$ (slightly beyond an onset of three-dimensionality at $\textit {Re} = 167.5$), where a secondary vortex street is observed by Ju & Jiang (2024).

3.3. Transient growth analysis of a circular cylinder wake

To relate the mean shear examined in § 3.1 to the existence/absence of the secondary vortex street in a more quantitative manner, transient growth analysis is performed, which quantifies integrated contribution of the mean shear in the wake.

Figure 6(a) summarises the optimal energy growth $G(\tau )$ computed with various $\textit {Re}$ values. For the laminar wakes, Jiang (2021b) found that the emergence of a secondary vortex street corresponded to $G(\tau )$ in the range $10^5$–$10^7$. For the 3-D wakes, the significantly reduced mean shear in the wake produces maximum $G(\tau )$ of merely $10^1$–$10^3$, which is several orders of magnitude smaller than the threshold of $G(\tau ) = O(10^5)$ (highlighted with a dashed line in figure 6a) for the emergence of the secondary vortex street. This analysis demonstrates that it is fundamentally impossible for these 3-D wakes to generate a secondary vortex street. It is also worth noting that even though the domain length downstream of the cylinder is finite (120$D$ for the present cases), the asymptotic $G(\tau )\unicode{x2013}\tau$ relationships demonstrate the absence of the secondary vortex street for any downstream location, which is a merit compared with flow visualisation or POD analysis.

Figure 6. Optimal energy growth $G(\tau )$ as a function of the time interval $\tau$ for various $\textit {Re}$ values: (a) results based on the time-averaged flow; and (b) comparison of results based on the time-averaged and instantaneous flows.

In addition, the validity of using the time-averaged flow for the transient growth analysis is examined in figure 6(b), where the transient growth analyses for $\textit {Re} = 200$ are also performed based on several instantaneous flows. Figure 6(b) shows that the use of time-averaged and instantaneous flows for the transient growth analysis yields similar results, such that the main conclusions are unaffected.

3.4. Secondary vortex streets in other bluff-body wakes

To generalise the present finding to other bluff-body wakes, several typical bodies other than a circular cylinder are considered, including square cylinders with incidence angles $0^\circ$ (called square cylinders for short) and $45^\circ$ (called diamond cylinders), and rectangular cylinders with $AR = 0.5$ and 0.0625 (and 1.0 for a square cylinder). For these bluff bodies, 2-D DNS were performed over a range of $\textit {Re}$ values, and the streamwise locations for the wake transitions to the two-layered and secondary vortex streets under the laminar wake assumption are summarised in figures 7(a) and 7(b), respectively. It is found that a thin rectangular cylinder (with $AR = 0.0625$) induces wake transitions closest to the bluff body, followed by the case of a diamond cylinder.

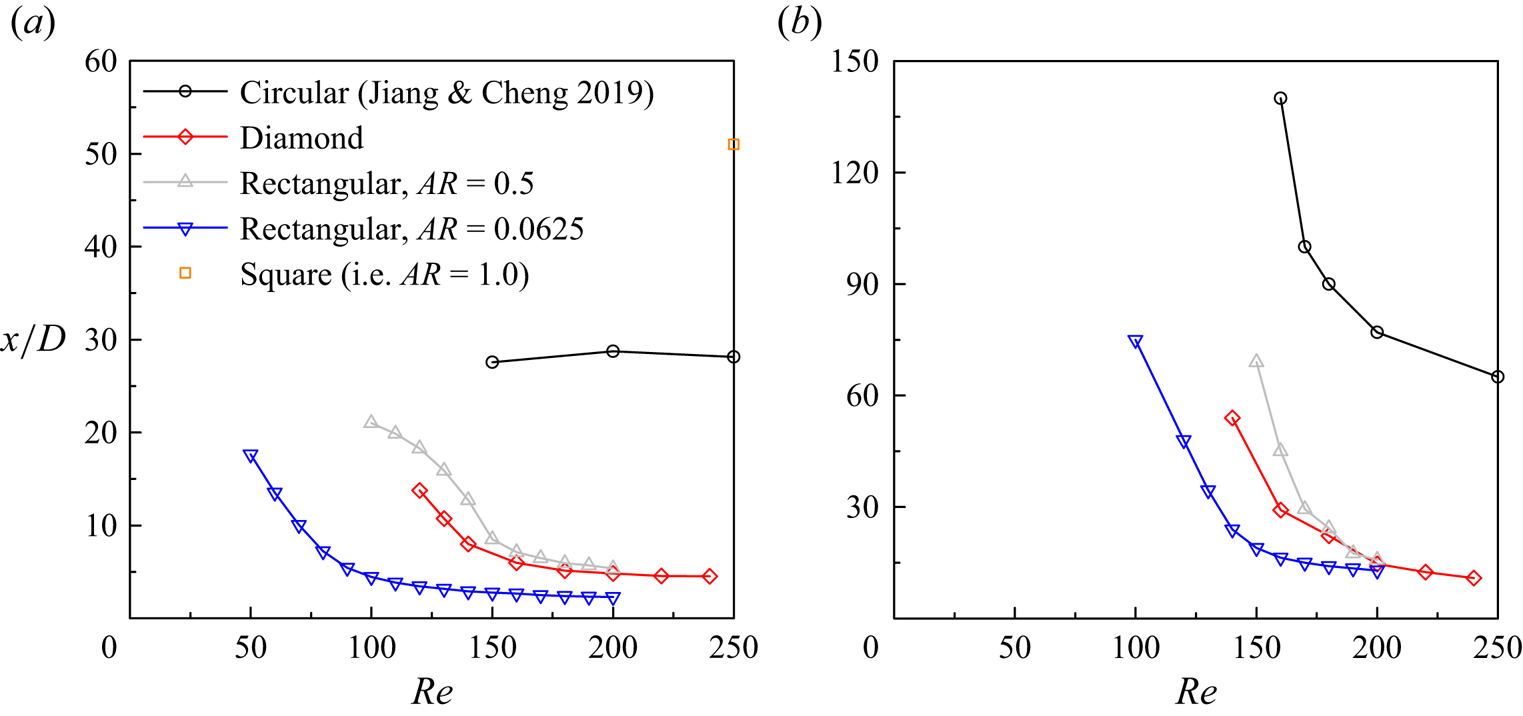
Figure 7. Streamwise locations for the two wake transitions behind different bluff bodies under the laminar wake assumption: (a) the first transition from the primary vortex street to the two-layered vortex street; and (b) earliest (in terms of the streamwise distance from the cylinder) detection of the second transition from the two-layered vortex street to the secondary vortex street.

Therefore, a thin rectangular cylinder with $AR = 0.0625$ and a diamond cylinder are selected for further demonstration of the absence of the secondary vortex street in 3-D wakes. For these two bluff bodies, the 3-D wake transitions occur at $\textit {Re} = 141$ (Choi & Yang 2014) and $\textit {Re} = 121$ (Jiang 2021a), respectively. Therefore, further analyses are focused on the 2-D wake at $\textit {Re} = 100$ and 3-D wake at $\textit {Re} = 300$. Figure 8(a) shows the streamwise variation of the maximum shear rate for different bluff-body wakes, while figure 8(b) shows the transient growth results. For the 2-D wakes at $\textit {Re} = 100$, a thin rectangular cylinder induces largest mean shear and transient growth in the wake, followed by diamond and circular cylinders, which explains the same sequencing of bluff bodies for the transition to the secondary vortex street observed in figure 7(b). For the 3-D wakes at $\textit {Re} = 300$, however, the thin rectangular and diamond cylinder wakes display shear rates and energy growths comparable to those of a circular cylinder. The saturation of $G(\tau )$ at $O(10^1)$ for these 3-D bluff-body wakes reinforces the conclusion that a secondary vortex street is absent in 3-D wakes (with the requirement that $\textit {Re}$ is not close to the onset of three-dimensionality). This conclusion is consistent with the observation in figure 1, where no secondary vortex street is observed.

Figure 8. Comparison among circular, thin rectangular (with $AR = 0.0625$) and diamond cylinder wakes: (a) streamwise variation of the maximum shear rate; and (b) optimal energy growth as a function of the time interval.

4. Conclusions

This study addresses the long-standing argument on the existence/absence of a secondary vortex street in 3-D and turbulent bluff-body wakes. We found that a secondary vortex street is absent for most 3-D and turbulent wakes.

For the case of a circular cylinder, the mean shear and perturbation energy growth in the wake are significantly reduced as the wake transitions from two to three dimensions, even before chaos and turbulence develop, which suggests that the main reason for the absence of secondary vortex street is the development of flow three-dimensionality, rather than spatiotemporal chaos or turbulence. However, flow three-dimensionality is not the root cause for the absence of secondary vortex street. The root cause is the weakening of spanwise vortices by 3-D wake instability modes and streamwise circulation/vorticity (so that under rare scenarios where the spanwise vortices are hardly affected by flow three-dimensionality, a secondary vortex street may be observed in 3-D flows). The weakened spanwise vortices over the two-layered vortex pattern induce reduced mean shear in the intermediate wake, which then induces much smaller perturbation energy growth that is below the threshold for the emergence of a secondary vortex street.

This conclusion is also generalised to various bluff-body flows, including those where the 2-D wakes produce stronger mean shear and thus earlier emergence of the secondary vortex street than those of a canonical circular cylinder. This finding also suggests that the 3-D and turbulence characteristics, and the momentum, mass and heat transport in the relatively far wake of bluff bodies, would not be influenced by extra anisotropy or inhomogeneity caused by a secondary vortex street.