Article contents
On standing gravity wave-depression cavity collapse and jetting
Published online by Cambridge University Press: 05 March 2019
Abstract
Parametrically forced gravity waves can give rise to high-velocity surface jets via the wave-depression cavity implosion. The present results have been obtained in circular cylindrical containers of 10 and 15 cm in diameter (Bond number of order 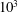 $10^{3}$) in the large fluid depth limit. First, the phase diagrams of instability threshold and wave breaking conditions are determined for the working fluid used, here water with 1 % detergent added. The collapse of the wave-depression cavity is found to be self-similar. The exponent
$10^{3}$) in the large fluid depth limit. First, the phase diagrams of instability threshold and wave breaking conditions are determined for the working fluid used, here water with 1 % detergent added. The collapse of the wave-depression cavity is found to be self-similar. The exponent  $\unicode[STIX]{x1D6FC}$ of the variation of the cavity radius
$\unicode[STIX]{x1D6FC}$ of the variation of the cavity radius 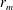 $r_{m}$ with time
$r_{m}$ with time  $\unicode[STIX]{x1D70F}$, in the form
$\unicode[STIX]{x1D70F}$, in the form 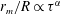 $r_{m}/R\propto \unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}$, is close to 0.5, indicative of inertial collapse, followed by a viscous cut-off of
$r_{m}/R\propto \unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}$, is close to 0.5, indicative of inertial collapse, followed by a viscous cut-off of 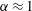 $\unicode[STIX]{x1D6FC}\approx 1$. This supports a Froude number scaling of the surface jet velocity caused by cavity collapse. The dimensionless jet velocity scales with the cavity depth that is shown to be proportional to the last stable wave amplitude. It can be expressed by a power law or in terms of finite time singularity related to a singular wave amplitude that sets the transition from a non-pinching to pinch-off cavity collapse scenario. In terms of forcing amplitude, cavity collapse and jetting are found to occur in bands of events of non-pinching and pinching of a bubble at the cavity base. At large forcing amplitudes, incomplete cavity collapse and splashing can occur and, at even larger forcing amplitudes, wave growth is again stable up to the singular wave amplitude. When the cavity is formed, an impulse model shows the importance of the singular cavity diameter that determines the strength of the impulse.
$\unicode[STIX]{x1D6FC}\approx 1$. This supports a Froude number scaling of the surface jet velocity caused by cavity collapse. The dimensionless jet velocity scales with the cavity depth that is shown to be proportional to the last stable wave amplitude. It can be expressed by a power law or in terms of finite time singularity related to a singular wave amplitude that sets the transition from a non-pinching to pinch-off cavity collapse scenario. In terms of forcing amplitude, cavity collapse and jetting are found to occur in bands of events of non-pinching and pinching of a bubble at the cavity base. At large forcing amplitudes, incomplete cavity collapse and splashing can occur and, at even larger forcing amplitudes, wave growth is again stable up to the singular wave amplitude. When the cavity is formed, an impulse model shows the importance of the singular cavity diameter that determines the strength of the impulse.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 9
- Cited by


