Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T03:12:06.234Z Has data issue: false hasContentIssue false
  • English
  • Français

On scaling pipe flows with sinusoidal transversely corrugated walls: analysis of data from the laminar to the low-Reynolds-number turbulent regime

Published online by Cambridge University Press:  14 August 2015

S. Saha ,
J. C. Klewicki ,
A. Ooi  and
H. M. Blackburn
S. Saha*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, VIC 3010, Australia
J. C. Klewicki
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, VIC 3010, Australia Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
A. Ooi
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, VIC 3010, Australia
H. M. Blackburn
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation was used to study laminar and turbulent flows in circular pipes with smoothly corrugated walls. The corrugation wavelength was kept constant at 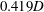$0.419D$, where 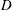$D$ is the mean diameter of the wavy-wall pipe and the corrugation height was varied from zero to 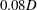$0.08D$. Flow rates were varied in steps between low values that generate laminar flow and higher values where the flow is in the post-transitional turbulent regime. Simulations in the turbulent regime were also carried out at a constant Reynolds number, 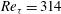$\mathit{Re}_{{\it\tau}}=314$, for all corrugation heights. It was found that even in the laminar regime, larger-amplitude corrugations produce flow separation. This leads to the proportion of pressure drop attributable to pressure drag being approximately 50 %, and rising to approximately 85 % in transitional rough-wall flow. The near-wall structure of turbulent flow is seen to be heavily influenced by the effects of flow separation and reattachment. Farther from the wall, the statistical profiles examined exhibit behaviours characteristic of smooth-wall flows or distributed roughness rough-wall flows. These observations support Townsend’s wall-similarity hypothesis. The organized nature of the present roughness allows the mean pressure drop to be written as a function of the corrugation height. When this is exploited in an analysis of the mean dynamical equation, the scaling problem is explicitly revealed to result from the combined influences of roughness and Reynolds number. The present results support the recent analysis and observations of Mehdi et al. (J. Fluid Mech., vol. 731, 2013, pp. 682–712), indicating that the length scale given by the distance from the wall at which the mean viscous force loses leading order is important to describing these combined influences, as well as providing a dynamically self-consistent connection to the scaling structure of smooth-wall pipe flow.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 779 , 25 September 2015 , pp. 245 - 274
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afzal, N. 2013 Roughness effects of commercial steel pipe in turbulent flow: universal scaling. Can. J. Civ. Engng 40 (2), 188–193.CrossRefGoogle Scholar
Afzal, N. & Seena, A. 2007 Alternate scales for turbulent flow in transitional rough pipes: universal log laws. Trans. ASME J. Fluids Engng 129 (1), 80–90.CrossRefGoogle Scholar
Afzal, N., Seena, A. & Bushra, A. 2006 Power law turbulent velocity profile in transitional rough pipes. Trans. ASME J. Fluids Engng 128 (3), 548–558.CrossRefGoogle Scholar
Afzal, N., Seena, A. & Bushra, A. 2013 Turbulent flow in a machine honed rough pipe for large Reynolds numbers: general roughness scaling laws. J. Hydro.-Environ. Res. 7 (1), 81–90.Google Scholar
Allen, J. J., Shockling, M. A., Kunkel, G. J. & Smits, A. J. 2007 Turbulent flow in smooth and rough pipes. Phil. Trans. R. Soc. Lond. A 365 (1852), 699–714.Google ScholarPubMed
Asako, Y. & Faghri, M. 1987 Finite-volume solutions for laminar flow and heat transfer in a corrugated duct. Transfer ASME J. Heat Trans. 109 (3), 627–634.Google Scholar
Bahaidarah, H. M. S., Anand, N. K. & Chen, H. C. 2005 Numerical study of heat and momentum transfer in channels with wavy walls. Numer. Heat Transfer A 47 (5), 417–439.Google Scholar
Benedict, R. P. 1980 Fundamentals of Pipe Flow. John Wiley.Google Scholar
Blackburn, H. M. 2002 Three-dimensional instability and state selection in an oscillatory axisymmetric swirling flow. Phys. Fluids 14 (11), 3983–3996.Google Scholar
Blackburn, H. M., Ooi, A. S. H. & Chong, M. S. 2007 The effect of corrugation height on flow in a wavy-walled pipe. In 16th Australasian Fluid Mechanics Conference, pp. 559–564. The University of Queensland, Gold Coast.Google Scholar
Blackburn, H. M. & Schmidt, S. 2003 Spectral element filtering techniques for large eddy simulation with dynamic estimation. J. Comput. Phys. 186 (2), 610–629.CrossRefGoogle Scholar
Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element – Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.CrossRefGoogle Scholar
Chin, C., Ooi, A. S. H., Marusic, I. & Blackburn, H. M. 2010 The influence of pipe length on turbulence statistics computed from direct numerical simulation data. Phys. Fluids 22 (11), 115107,1-10.CrossRefGoogle Scholar
Chung, D., Monty, J. P. & Ooi, A. 2014 An idealised assessment of Townsend’s outer-layer similarity hypothesis for wall turbulence. J. Fluid Mech. 742, R3-1–R3-12.Google Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aero. Sci. 21, 91–108.Google Scholar
Cookson, A. N., Doorly, D. J. & Sherwin, S. J. 2009 Mixing through stirring of steady flow in small amplitude helical tubes. Ann. Biomed. Engng 37 (4), 710–721.CrossRefGoogle ScholarPubMed
Cotrell, D. L., MacFadden, G. B. & Alder, B. J. 2008 Instability in pipe flow. Proc. Natl Acad. Sci. USA 105 (2), 428–430.CrossRefGoogle ScholarPubMed
De Marchis, M. & Napoli, E. 2012 Effects of irregular two-dimensional and three-dimensional surface roughness in turbulent channel flows. Intl J. Heat Fluid Flow 36, 7–17.Google Scholar
Eiamsa-ard, S. & Promvonge, P. 2007 Enhancement of heat transfer in a circular wavy-surfaced tube with a helical-tape insert. Intl Energy J. 8 (1), 29–36.Google Scholar
Faghri, M. & Asako, Y. 1987 Numerical determination of heat transfer and pressure drop characteristics for converging–diverging flow channel. Trans. ASME J. Heat Transfer 109, 606–612.Google Scholar
Fife, P., Klewicki, J. C. & Wei, T. 2009 Time averaging in turbulence settings may reveal an infinite hierarchy of length scales. J. Discrete Continuous Dyn. Syst. 24, 781–807.Google Scholar
Flack, K. A. & Schultz, M. P. 2010 Review of hydraulic roughness scales in the fully rough regime. Trans. ASME J. Fluids Engng 132, 041203.Google Scholar
Flack, K. A., Schultz, M. P. & Shapiro, T. A. 2005 Experimental support for Townsend’s Reynolds number similarity hypothesis on rough walls. Phys. Fluids 17, 035102.CrossRefGoogle Scholar
Gioia, G., Chakraborty, P. & Bombardelli, F. A. 2006 Rough-pipe flows and the existence of fully developed turbulence. Phys. Fluids 18, 038107.Google Scholar
Granville, P. S. 1987 Three indirect methods for the drag characterization of arbitrarily rough surfaces on flat plates. J. Ship Res. 31 (1), 70–77.Google Scholar
Guermond, J. L. & Shen, J. 2003 Velocity-correction projection methods for incompressible flows. SIAM J. Numer. Anal. 41 (1), 112–134.Google Scholar
Guzmán, A. M., Cárdenas, M. J., Urzúa, F. A. & Araya, P. E. 2009 Heat transfer enhancement by flow bifurcations in asymmetric wavy wall channels. Intl J. Heat Mass Transfer 52 (15), 3778–3789.Google Scholar
Hama, F. R. 1954 Boundary-layer characteristics for smooth and rough surfaces. Trans. Soc. Nav. Archit. Mar. Engrs 62, 333–358.Google Scholar
Hossain, M. Z. & Islam, A. K. M. S. 2004 Numerical investigation of unsteady flow and heat transfer in wavy channels. In The 15th Australasian Fluid Mechanics Conference, pp. 13–17. The University of Sydney.Google Scholar
Hwang, S. D., Jang, I. H. & Cho, H. H. 2006 Experimental study on flow and local heat/mass transfer characteristics inside corrugated duct. Intl J. Heat Fluid Flow 27 (1), 21–32.Google Scholar
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Kern, W. F. & Bland, J. R. 1948 Theorem of pappus. In Solid Mensuration with Proofs, 2nd edn. pp. 110–115. John Wiley & Sons.Google Scholar
Klewicki, J. C. 2013a A description of turbulent wall-flow vorticity consistent with mean dynamics. J. Fluid Mech. 737, 176–204.Google Scholar
Klewicki, J. C. 2013b Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.Google Scholar
Klewicki, J. C., Chin, C., Blackburn, H. M., Ooi, A. S. H. & Marusic, I. 2012 Emergence of the four layer dynamical regime in turbulent pipe flow. Phys. Fluids 24, 045107.Google Scholar
Leonardi, S., Orlandi, P., Smalley, R., Djenidi, L. & Antonia, R. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.Google Scholar
Loh, S. A. & Blackburn, H. M. 2011 Stability of steady flow through an axially corrugated pipe. Phys. Fluids 23, 111703-1–4.Google Scholar
Mehdi, F., Klewicki, J. C. & White, C. M. 2010 Mean momentum balance analysis of rough-wall turbulent boundary layers. Physica D 239 (14), 1329–1337.Google Scholar
Mehdi, F., Klewicki, J. C. & White, C. M. 2013 Mean force structure and its scaling in rough-wall turbulent boundary layers. J. Fluid Mech. 731, 682–712.Google Scholar
Millikan, C. B. 1938 A critical discussion of turbulent flow in channels and circular tubes. In 5th International Congress for Applied Mechanics (ed. den Hartog, J. P. & Peters, H.), pp. 386–392. Wiley/Chapman & Hall.Google Scholar
Napoli, E., Armenio, V. & De Marchis, M. 2008 The effect of the slope of irregularly distributed roughness elements on turbulent wall-bounded flows. J. Fluid Mech. 613, 385–394.CrossRefGoogle Scholar
Nikuradse, J.1933 Laws of flow in rough pipes. VDI Forschungsheft 361; also NACA TM 1292, 1950.Google Scholar
O’Brien, J. E. 1982 Corrugated duct heat transfer, pressure drop and flow visualization. Trans. ASME J. Heat Transfer 104, 410–416.Google Scholar
Piomelli, U. 1997 Large-eddy simulations: where we stand. In Advances in DNS/LES (ed. Liu, C. & Liu, Z.), pp. 93–104. AFOSR.Google Scholar
Popiel, C. O. & Van der Merwe, D. F. 1996 Friction factor in sine-pipe flow. Trans. ASME J. Fluids Engng 118 (2), 341–345.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.Google Scholar
Saha, S., Chin, C., Blackburn, H. M. & Ooi, A. S. H. 2011 The influence of pipe length on thermal statistics computed from DNS of turbulent heat transfer. Intl J. Heat Fluid Flow 32 (6), 1083–1097.Google Scholar
Sawyers, D. R., Sen, M. & Chang, H.-C. 1998 Heat transfer enhancement in three-dimensional corrugated channel flow. Intl J. Heat Mass Transfer 41 (22), 3559–3573.Google Scholar
Schlichting, H. 1936 Experimentelle Untersuchungen zum Rahigkeitsproblem. Ing.-Arch. 7, 1–34.Google Scholar
Schmidt, S., McIver, D. M., Blackburn, H. M., Rudman, M. & Nathan, G. J. 2001 Spectral element based simulation of turbulent pipe flow. In 14th Australasian Fluid Mechanics Conference, pp. 9–14. Adelaide University.Google Scholar
Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21 (1), 015104-1–9.Google Scholar
Schultz, M. P. & Myers, A. 2003 Comparison of three roughness function determination methods. Exp. Fluids 35 (4), 372–379.Google Scholar
Seena, A. & Afzal, N. 2008 Intermediate scaling of turbulent momentum and heat transfer in a transitional rough channel. Trans. ASME J. Heat Transfer 130 (3), 031701.CrossRefGoogle Scholar
Shimizu, Y., Sugino, K., Kuzuhara, S. & Murakami, M. 1982 Hydraulic losses and flow patterns in bent pipes: comparison of the results in wavy pipes and quasi-coiled ones. Bull. JSME 25 (199), 24–31.Google Scholar
Shockling, M. A., Allen, J. J. & Smits, A. J. 2006 Roughness effects in turbulent pipe flow. J. Fluid Mech. 564 (1), 267–285.Google Scholar
Sparrow, E. M. & Prata, A. T. 1983 Numerical solutions for laminar flow and heat transfer in a periodically converging-diverging tube, with experimental confirmation. Numer. Heat Transfer A 6 (4), 441–461.Google Scholar
Sui, Y., Teo, C. J. & Lee, P. S. 2012 Direct numerical simulation of fluid flow and heat transfer in periodic wavy channels with rectangular cross-sections. Intl J. Heat Mass Transfer 55 (1), 73–88.CrossRefGoogle Scholar
Tatsuo, N., Shinichiro, M., Shingho, A. & Yuji, K. 1990 Flow observations and mass transfer characteristics in symmetrical wavy-walled channels at moderate Reynolds numbers for steady flow. Intl J. Heat Mass Transfer 33 (5), 835–845.Google Scholar
den Toonder, J. M. J. & Nieuwstadt, F. T. M. 1997 Reynolds number effects in a turbulent pipe flow for low to moderate $Re$ . Phys. Fluids 9 (11), 3398–3409.CrossRefGoogle Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tuckerman, L. S. & Barkley, D. 2000 Bifurcation analysis for timesteppers. In Numerical Methods for Bifurcation Problems and Large-Scale Dynamical Systems (ed. Doedel, E. & Tuckerman, L. S.), pp. 453–566. Springer.Google Scholar
Wang, L.-P. & Du, M. H. 2008 Direct simulation of viscous flow in a wavy pipe using the lattice Boltzmann approach. Intl J. Engng Syst. Model. Simul. 1 (1), 20–29.Google Scholar
Wei, T., Fife, P., Klewicki, J. C. & McMurtry, P. 2005a Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Wei, T., McMurtry, P., Klewicki, J. C. & Fife, P. 2005b Mesoscaling of Reynolds shear stress in turbulent channel and pipe flows. AIAA J. 43 (11), 2350–2353.Google Scholar
Westerweel, J.1993 Digital particle image velocimetry. PhD thesis, Delft University.Google Scholar
Wu, Y. & Christensen, K. T. 2007 Outer-layer similarity in the presence of a practical rough-wall topography. Phys. Fluids 19, 085108.Google Scholar