Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T18:57:38.388Z Has data issue: false hasContentIssue false
  • English
  • Français

On non-Oberbeck–Boussinesq effects in Rayleigh–Bénard convection of air for large temperature differences

Published online by Cambridge University Press:  21 February 2020

Zhen-Hua Wan Open the ORCID record for Zhen-Hua Wan [Opens in a new window] ,
Qi Wang Open the ORCID record for Qi Wang [Opens in a new window] ,
Ben Wang ,
Shu-Ning Xia ,
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window]  and
De-Jun Sun
Zhen-Hua Wan
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230027, PR China
Qi Wang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230027, PR China
Ben Wang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230027, PR China
Shu-Ning Xia
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai200072, PR China
Quan Zhou
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai200072, PR China
De-Jun Sun*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230027, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present direct numerical simulations of non-Oberbeck–Boussinesq (NOB) Rayleigh–Bénard (RB) convection due to large temperature differences in two-dimensional (2-D) and three-dimensional (3-D) cells. Perfect air is chosen as the operating fluid and the Prandtl number ($Pr$) is fixed to 0.71 for the reference state $\hat{T}_{0}=300~\text{K}$. In the present system, we consider large temperature differences ranging from 60 K to 240 K, and relatively strong NOB effects are induced at moderate Rayleigh numbers ($Ra$) in the range $3\times 10^{6}\leqslant Ra\leqslant 5\times 10^{9}$. The large temperature difference also induces the turbulence system with large density variation. Due to top-down symmetry breaking under NOB conditions, an increase of the centre temperature $T_{c}$ is found compared to the arithmetic mean temperature $T_{m}$ of the top and bottom plates, and the shift of $T_{c}$ is strongly dependent on Rayleigh number $Ra$ and temperature differential $\unicode[STIX]{x1D716}$. The NOB effects on the Nusselt number ($Nu$) are quite small (${\lesssim}2\,\%$). The power-law scalings of $Nu$ versus $Ra$ are robust against NOB effects, even for the extremely large temperature difference 240 K, which has never been reached in previous experiments and simulations. The Reynolds numbers $Re$, as well as the scalings of $Re$ versus $Ra$, are also insensitive to NOB effects. It is noteworthy that the influence of NOB effects on $Nu$ and $Re$ in 3-D RB flow are weaker than its 2-D counterpart. Furthermore, the extended laminar boundary layer (BL) equations are developed based on the low-Mach-number Navier–Stokes equations, which qualitatively predicts the NOB effects on velocity profiles. Direct numerical simulation results indicate that the top and bottom thermal BLs can compensate each other much better than the velocity BLs under NOB conditions, which contribute to the robustness of $Nu$.

JFM classification

Convection: Convection in cavities
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 889 , 25 April 2020 , A10
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2007 Non-Oberbeck–Boussinesq effects in gaseous Rayleigh–Bénard convection. Phys. Rev. Lett. 98 (5), 054501.CrossRefGoogle ScholarPubMed
Ahlers, G., Brown, E., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck–Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.CrossRefGoogle Scholar
Ahlers, G., Calzavarini, E., Araujo, F. F., Funfschilling, D., Grossmann, S., Lohse, D. & Sugiyama, K. 2008 Non-Oberbeck–Boussinesq effects in turbulent thermal convection in ethane close to the critical point. Phys. Rev. E 77 (4), 046302.Google ScholarPubMed
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1994 Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 50 (1), 269.Google ScholarPubMed
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32 (1), 709–778.CrossRefGoogle Scholar
Briggs, W. L., Henson, V. E. & McCormick, S. F. 2000 A Multigrid Tutorial, vol. 72. SIAM.CrossRefGoogle Scholar
Brown, E., Funfschilling, D. & Ahlers, G. 2007 Anomalous Reynolds-number scaling in turbulent Rayleigh–Bénard convection. J. Stat. Mech. 2007 (10), P10005.CrossRefGoogle Scholar
Burnishev, Y., Segre, E. & Steinberg, V. 2010 Strong symmetrical non-Oberbeck–Boussinesq turbulent convection and the role of compressibility. Phys. Fluids 22 (3), 035108.CrossRefGoogle Scholar
Burnishev, Y. & Steinberg, V. 2012 Statistics and scaling properties of temperature field in symmetrical non-Oberbeck–Boussinesq turbulent convection. Phys. Fluids 24 (4), 045102.CrossRefGoogle Scholar
Chandra, M. & Verma, M. K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110 (11), 114503.CrossRefGoogle ScholarPubMed
Chen, L.-W., Xu, C.-Y. & Lu, X.-Y. 2010 Numerical investigation of the compressible flow past an aerofoil. J. Fluid Mech. 643, 97–126.CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 1–25.CrossRefGoogle ScholarPubMed
Demou, A. D. & Grigoriadis, D. G. E. 2019 Direct numerical simulations of Rayleigh–Bénard convection in water with non-Oberbeck–Boussinesq effects. J. Fluid Mech. 881, 1073–1096.CrossRefGoogle Scholar
Gray, D. D. & Giorgini, A. 1976 The validity of the Boussinesq approximation for liquids and gases. Intl J. Heat Mass Transfer 19 (5), 545–551.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26 (5), 055111.CrossRefGoogle Scholar
Horn, S., Shishkina, O. & Wagner, C. 2013 On non-Oberbeck–Boussinesq effects in three-dimensional Rayleigh–Bénard convection in glycerol. J. Fluid Mech. 724, 175–202.CrossRefGoogle Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102 (6), 064501.CrossRefGoogle ScholarPubMed
Liu, S., Xia, S.-N., Yan, R., Wan, Z.-H. & Sun, D.-J. 2018 Linear and weakly nonlinear analysis of Rayleigh–Bénard convection of perfect gas with non-Oberbeck–Boussinesq effects. J. Fluid Mech. 845, 141–169.CrossRefGoogle Scholar
Livescu, D. 2020 Turbulence with large thermal and compositional density variations. Annu. Rev. Fluid Mech. 52, 309–341.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Lui, S.-L. & Xia, K.-Q. 1998 Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 57 (5), 5494.Google Scholar
Ng, C. S., Ooi, A., Lohse, D. & Chung, D. 2018 Bulk scaling in wall-bounded and homogeneous vertical natural convection. J. Fluid Mech. 841, 825–850.CrossRefGoogle Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.CrossRefGoogle Scholar
Paolucci, S.1982 Filtering of sound from the Navier–Stokes equations. NASA STI Tech. Rep. Recon Tech. Rep. N, 83, 26036.Google Scholar
Pirozzoli, S., Bernardini, M. & Grasso, F. 2010 Direct numerical simulation of transonic shock/boundary layer interaction under conditions of incipient separation. J. Fluid Mech. 657, 361–393.CrossRefGoogle Scholar
van der Poel, E. P., Ostilla-Mnico, R., Donners, J. & Verzicco, R. 2015 A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids 116, 10–16.CrossRefGoogle Scholar
van der Poel, E. P., Stevens, R. J. A. M., Sugiyama, K. & Lohse, D. 2012 Flow states in two-dimensional Rayleigh–Bénard convection as a function of aspect-ratio and Rayleigh number. Phys. Fluids 24 (8), 085104.CrossRefGoogle Scholar
Qiu, X.-L. & Tong, P. 2001 Large-scale velocity structures in turbulent thermal convection. Phys. Rev. E 64 (3), 036304.Google ScholarPubMed
Sameen, A., Verzicco, R. & Sreenivasan, K. R. 2008 Non-Boussinesq convection at moderate Rayleigh numbers in low temperature gaseous helium. Phys. Scr. 2008 (T132), 014053.Google Scholar
Sameen, A., Verzicco, R. & Sreenivasan, K. R. 2009 Specific roles of fluid properties in non-Boussinesq thermal convection at the Rayleigh number of 2 × 108. Eur. Phys. Lett. 86 (1), 14006.CrossRefGoogle Scholar
Shi, N., Emran, M. S. & Schumacher, J. 2012 Boundary layer structure in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 706, 5–33.CrossRefGoogle Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.CrossRefGoogle Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2007 Non-Oberbeck–Boussinesq effects in two-dimensional Rayleigh–Bénard convection in glycerol. Eur. Phys. Lett. 80 (3), 34002.CrossRefGoogle Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2009 Flow organization in two-dimensional non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. J. Fluid Mech. 637, 105–135.CrossRefGoogle Scholar
Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
Sun, C. & Xia, K.-Q. 2005 Scaling of the Reynolds number in turbulent thermal convection. Phys. Rev. E 72 (6), 067302.Google ScholarPubMed
Suslov, S. A. 2010 Mechanism of nonlinear flow pattern selection in moderately non-Boussinesq mixed convection. Phys. Rev. E 81 (2), 026301.Google ScholarPubMed
Suslov, S. A. & Paolucci, S. 1999 Nonlinear stability of mixed convection flow under non-Boussinesq conditions. Part 1. Analysis and bifurcations. J. Fluid Mech. 398, 61–85.CrossRefGoogle Scholar
Sutherland, W. 1893 The viscosity of gases and molecular force. Lond. Edinb. Dublin Phil. Mag. J. Sci. 36, 507–531.CrossRefGoogle Scholar
Valori, V., Elsinga, G., Rohde, M., Tummers, M., Westerweel, J. & van der Hagen, T. 2017 Experimental velocity study of non-Boussinesq Rayleigh–Bénard convection. Phys. Rev. E 95 (5), 053113.Google ScholarPubMed
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.CrossRefGoogle Scholar
Wagner, S. & Shishkina, O. 2013 Aspect-ratio dependency of Rayleigh–Bénard convection in box-shaped containers. Phys. Fluids 25 (8), 085110.CrossRefGoogle Scholar
Wan, Z.-H., Zhou, L., Yang, H.-H. & Sun, D.-J. 2013 Large eddy simulation of flow development and noise generation of free and swirling jets. Phys. Fluids 25 (12), 126103.CrossRefGoogle Scholar
Wang, Q., Xia, S.-N., Wang, B.-F., Sun, D.-J., Zhou, Q. & Wan, Z.-H. 2018 Flow reversals in two-dimensional thermal convection in tilted cells. J. Fluid Mech. 849, 355–372.CrossRefGoogle Scholar
Wang, Q., Xia, S.-N., Yan, R., Sun, D.-J. & Wan, Z.-H. 2019a Non-Oberbeck-Boussinesq effects due to large temperature differences in a differentially heated square cavity filled with air. Intl J. Heat Mass Transfer 128, 479–491.CrossRefGoogle Scholar
Wang, Q., Zhou, Q., Wan, Z.-H. & Sun, D.-J. 2019b Penetrative turbulent Rayleigh–Bénard convection in two and three dimensions. J. Fluid Mech. 870, 718–734.CrossRefGoogle Scholar
Wei, P. & Xia, K.-Q. 2013 Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting. J. Fluid Mech. 720, 140–168.CrossRefGoogle Scholar
Weiss, S., He, X., Ahlers, G., Bodenschatz, E. & Shishkina, O. 2018 Bulk temperature and heat transport in turbulent Rayleigh–Bénard convection of fluids with temperature-dependent properties. J. Fluid Mech. 851, 374–390.CrossRefGoogle Scholar
White, F. M. 1974 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Wu, X.-Z. & Libchaber, A.1991 Non-Boussinesq effects in free thermal convection. 43 (6), 2833–2839.Google Scholar
Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.CrossRefGoogle Scholar
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 05, 3–14.Google Scholar
Xia, S.-N., Wan, Z.-H., Liu, S., Wang, Q. & Sun, D.-J. 2016 Flow reversals in Rayleigh–Bénard convection with non-Oberbeck–Boussinesq effects. J. Fluid Mech. 798, 628–642.CrossRefGoogle Scholar
Zhang, J., Childress, S. & Libchaber, A. 1997 Non-Boussinesq effect: thermal convection with broken symmetry. Phys. Fluids 9 (4), 1034–1042.CrossRefGoogle Scholar
Zhang, J., Childress, S. & Libchaber, A. 1998 Non-Boussinesq effect: asymmetric velocity profiles in thermal convection. Phys. Fluids 10 (6), 1534–1536.CrossRefGoogle Scholar
Zhang, Y., Zhou, Q. & Sun, C. 2017 Statistics of kinetic and thermal energy dissipation rates in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 814, 165–184.CrossRefGoogle Scholar
Zhang, Y.-Z., Sun, C., Bao, Y. & Zhou, Q. 2018 How surface roughness reduces heat transport for small roughness heights in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 836, R2.CrossRefGoogle Scholar
Zhou, Q. & Xia, K.-Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.CrossRefGoogle Scholar

Wan et al. supplementary movie 1

The distribution of temperature and velocity vectors at Ra=5e8 for OB case

Download Wan et al. supplementary movie 1(Video)
Video 4.2 MB

Wan et al. supplementary movie 2

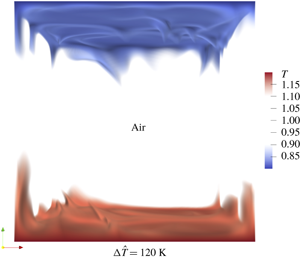
The distribution of temperature and velocity vectors at Ra=5e8 for ε=0.2

Download Wan et al. supplementary movie 2(Video)
Video 3.6 MB

Wan et al. supplementary movie 3

The distribution of temperature and velocity vectors at Ra=8e8 for OB case

Download Wan et al. supplementary movie 3(Video)
Video 12 MB

Wan et al. supplementary movie 4

The distribution of temperature and velocity vectors at Ra=8e8 for ε=0.2

Download Wan et al. supplementary movie 4(Video)
Video 12.5 MB