Article contents
On models for predicting thermodynamic regimes in high-pressure turbulent mixing and combustion of multispecies mixtures
Published online by Cambridge University Press: 23 March 2018
Abstract
The thermodynamic regime of a complex mixture depends on the composition, the pressure and the temperature; the spinodal locus separates the regime of thermodynamic instability from the remainder of the phase space. Since diffusion is one of the phenomena affecting the local chemical composition, the first focus is here on evaluating diffusion models in the context of high-pressure (high-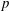 $p$) multispecies mixing and combustion. It is shown that the diffusion model equations previously used to create two high-
$p$) multispecies mixing and combustion. It is shown that the diffusion model equations previously used to create two high-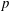 $p$ direct numerical simulation (DNS) databases can reproduce classical experimental observations of uphill diffusion in an accurate spatiotemporal manner, whereas the popular model which has a diagonal diffusion matrix and uses a velocity correction lacks spatiotemporal accuracy. Further, a mathematical formalism is used to compute the spinodal locus for mixtures for which either experimental data or previous computations from the literature are available, and it is shown that the agreement of the present calculations with that previously existing information is excellent. Using the spinodal-calculation mathematical formalism, the aforementioned DNS databases are then examined to determine the thermodynamic regime of the mixture at important stages of the simulations. In the first subset of the DNS databases that portrays mixing of five species under high-
$p$ direct numerical simulation (DNS) databases can reproduce classical experimental observations of uphill diffusion in an accurate spatiotemporal manner, whereas the popular model which has a diagonal diffusion matrix and uses a velocity correction lacks spatiotemporal accuracy. Further, a mathematical formalism is used to compute the spinodal locus for mixtures for which either experimental data or previous computations from the literature are available, and it is shown that the agreement of the present calculations with that previously existing information is excellent. Using the spinodal-calculation mathematical formalism, the aforementioned DNS databases are then examined to determine the thermodynamic regime of the mixture at important stages of the simulations. In the first subset of the DNS databases that portrays mixing of five species under high-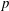 $p$ conditions, this stage is that of the transitional state representing the individual time station at which each simulation, having been initiated in a laminar state, transitions to a state having turbulent characteristics. In the second subset of the DNS databases that portrays high-
$p$ conditions, this stage is that of the transitional state representing the individual time station at which each simulation, having been initiated in a laminar state, transitions to a state having turbulent characteristics. In the second subset of the DNS databases that portrays high-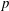 $p$ turbulent combustion, this stage represents the individual time station at the peak
$p$ turbulent combustion, this stage represents the individual time station at the peak 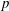 $p$ achieved during the calculations. In both databases, the influence of the initial Reynolds number, the free-stream composition and the free-stream
$p$ achieved during the calculations. In both databases, the influence of the initial Reynolds number, the free-stream composition and the free-stream 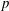 $p$ is studied. The results show that in all cases the mixture is in the single-phase regime. The present DNS databases have only five species, but it is shown that the methodology for computing the spinodal locus can be applied to very complex mixtures, with examples given for a twelve-species mixture and surrogate diesel fuels, thereby boding well for determining the thermodynamic regime of practical mixtures in high-
$p$ is studied. The results show that in all cases the mixture is in the single-phase regime. The present DNS databases have only five species, but it is shown that the methodology for computing the spinodal locus can be applied to very complex mixtures, with examples given for a twelve-species mixture and surrogate diesel fuels, thereby boding well for determining the thermodynamic regime of practical mixtures in high-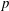 $p$ turbulent flow simulations for engineering applications. According to these calculations, diesel-fuel surrogates are always in the single-phase regime at injection-conditions
$p$ turbulent flow simulations for engineering applications. According to these calculations, diesel-fuel surrogates are always in the single-phase regime at injection-conditions 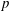 $p$ and temperatures existing in diesel-engine combustion chambers.
$p$ and temperatures existing in diesel-engine combustion chambers.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 15
- Cited by


