Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T22:48:14.099Z Has data issue: false hasContentIssue false
  • English
  • Français

On Langmuir circulation in 1 : 2 and 1 : 3 resonance

Published online by Cambridge University Press:  09 October 2019

L. Cui  and
W. R. C. Phillips Open the ORCID record for W. R. C. Phillips [Opens in a new window]
L. Cui
Affiliation:
Department of Mathematics, Swinburne University of Technology, Hawthorn, VIC 3122, Australia
W. R. C. Phillips*
Affiliation:
Department of Mathematics, Swinburne University of Technology, Hawthorn, VIC 3122, Australia Department of Theoretical and Applied Mechanics, University of Illinois at Urbana-Champaign, Urbana, IL 61801-2935, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the nonlinear dynamics of spanwise periodic longitudinal vortex modes (Langmuir circulation (LC)) that arise through the instability of two-dimensional periodic flows (waves) in a non-stratified uniformly sheared layer of finite depth. Of particular interest is the excitation of the vortex modes either in the absence of interaction or in resonance, as described by nonlinear amplitude equations built upon the mean field Craik–Leibovich (CL) equations. Since Y-junctions in the surface footprints of Langmuir circulation indicate sporadic increases (doubling) in spacing as they evolve to the scale of sports stadiums, interest is focused on bifurcations that instigate such changes. To that end, surface patterns arising from the linear and nonlinear excitation of the vortex modes are explored, subject to two parameters: a Rayleigh number 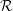${\mathcal{R}}$ present in the CL equations and a symmetry breaking parameter 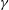$\unicode[STIX]{x1D6FE}$ in the mixed free surface boundary conditions that relax to those at the layer bottom where 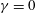$\unicode[STIX]{x1D6FE}=0$. Looking first to linear instability, it is found as 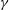$\unicode[STIX]{x1D6FE}$ increases from zero to unity, that the neutral curves evolve from asymmetric near onset to almost symmetric. The nonlinear dynamics of single modes is then studied via an amplitude equation of Ginzburg–Landau type. While typically of cubic order when the bifurcation is supercritical (as it is here) and the neutral curves are parabolic, the Ginzburg–Landau equation must instead here be of quartic order to recover the asymmetry in the neutral curves. This equation is then subjected to an Eckhaus instability analysis, which indicates that linearly unstable subharmonics mostly reside outside the Eckhaus boundary, thereby excluding them as candidates for excitation. The surface pattern is then largely unchanged from its linear counterpart, although the character of the pattern does change when 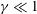$\unicode[STIX]{x1D6FE}\ll 1$ as a result of symmetry breaking. Attention is then turned to strong resonance between the least stable linear mode and a sub-harmonic of it, as described by coupled nonlinear amplitude equations of Stuart-Landau type. Both 1 : 2 and 1 : 3 resonant interactions are considered. Phase plots and bifurcation diagrams are employed to reveal classes of solution that can occur. Dominant over much of the ${\mathcal{R}}$-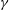$\unicode[STIX]{x1D6FE}$ range considered are non-travelling pure- and mixed-mode equilibrium solutions that act singly or together. To wit, pure modes solutions alone act to realise windrows with spacings in accord with linear theory, while bistability can realise Y-junctions and, depending upon initial conditions, double or even triple the dominant spacing of LC.

JFM classification

Instability: Nonlinear instability Nonlinear Dynamical Systems: Pattern formation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 353 - 387
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. G. & McIntyre, M. E. 1978 An exact theory of nonlinear waves on a Lagrangian-mean flow. J. Fluid Mech. 89, 609–646.Google Scholar
Armbruster, D., Guckenheimer, J. & Holmes, P. 1988 Heteroclinic cycles and modulated travelling waves in systems with O (2) symmetry. Physica D 29, 257–282.Google Scholar
Babanin, A. V., Ganopolski, A. & Phillips, W. R. C. 2009 Wave-induced upper-ocean mixing in a climate model of intermediate complexity. Ocean Model. 29, 189–197.Google Scholar
Barstow, S. F. 1983 The ecology of Langmuir circulation: a review. Mar. Environ. Res. 9, 211–236.Google Scholar
Bhaskaran, R. & Leibovich, S. 2002 Eulerian and Lagrangian Langmuir circulation patterns. Phys. Fluids 14, 2557–2571.Google Scholar
Chini, G. P. & Leibovich, S. 2003 Resonant Langmuir-circulation-internal-wave interaction. Part 1. Internal wave reflection. J. Fluid Mech. 495, 35–55.Google Scholar
Chini, G. P. & Leibovich, S. 2005 Resonant Langmuir-circulation-internal-wave interaction. Part 2. Langmuir circulation instability. J. Fluid Mech. 524, 99–120.Google Scholar
Cox, S. M. 1996 Mode interactions in Rayleigh–Bénard convection. Physica D 95, 50–61.Google Scholar
Cox, S. M. & Leibovich, S. 1993 Langmuir circulations in a surface layer bounded by a strong thermocline. J. Phys. Oceanogr. 23, 1330–1345.Google Scholar
Cox, S. M. & Leibovich, S. 1994 Large-scale Langmuir circulation and double-diffusive convection: evolution equations and flow transitions. J. Fluid Mech. 276, 189–210.Google Scholar
Cox, S. M., Leibovich, S., Moroz, I. M. & Tandon, A. 1992a Hopf bifurcations in Langmuir circulations. Physica D 59, 226–254.Google Scholar
Cox, S. M., Leibovich, S., Moroz, I. M. & Tandon, A. 1992b Nonlinear dynamics in Langmuir circulations with O (2) symmetry. J. Fluid Mech. 241, 669–704.Google Scholar
Craik, A. D. D. 1977 The generation of Langmuir circulations by an instability mechanism. J. Fluid Mech. 81, 209–223.Google Scholar
Craik, A. D. D. 1985 Waves Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Craik, A. D. D. & Leibovich, S. 1976 A rational model for Langmuir circulations. J. Fluid Mech. 73, 401–426.Google Scholar
Crouch, J. D. & Herbert, T. 1993 A note on the calculation of Landau constants. Phys. Fluids A 5, 283–285.Google Scholar
Dangelmayr, G. 1986 Steady-state mode interactions in the presence of 0(2)-symmetry. Dyn. Stab. Syst. 1, 159–185.Google Scholar
Deguchi, K. & Hall, P. 2014 The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow. J. Fluid Mech. 750, 99–112.Google Scholar
Doelman, A. & Eckhaus, W. 1991 Periodic and quasi-periodic solutions of degenerate modulation equations. Physica D 53, 249–266.Google Scholar
Eckhaus, W. & Iooss, G. 1989 Strong selection or rejection of spatially periodic patterns in degenerate bifurcations. Physica D 39, 124–146.Google Scholar
Faller, A. J. 1978 Experiments with controlled Langmuir circulations. Science 201, 618–620.Google Scholar
Faller, A. J. & Caponi, E. A. 1978 Laboratory studies of wind-driven Langmuir circulations. J. Geophys. Res. 83, 3617–3633.Google Scholar
Farmer, D. & Li, M. 1995 Patterns of bubble clouds organized by Langmuir circulation. J. Phys. Oceanogr. 25, 1426–1440.Google Scholar
Fujimura, K. & Nagata, M. 1998 Degenerate 1 : 2 steady state mode interaction – MHD flow in a vertical slot. Physica D 115, 377–400.Google Scholar
Gill, A. E. 1982 Atmosphere-Ocean Dynamics. Elsevier.Google Scholar
Ginzburg, V. L. & Landau, L. D. 1950 On the theory of superconductivity. Zh. Eksp. Teor. Fiz. 20, 1064–1082.Google Scholar
Hall, P. 1983 The linear development of Görtler vortices in growing boundary layers. J. Fluid Mech. 130, 41–58.Google Scholar
Hall, P. & Smith, F. 1988 The nonlinear interaction of Görtler vortices and Tollmien–Schlichting waves in curved channel flows. Proc. R. Soc. Lond. A 417, 255–282.Google Scholar
Hayes, D. T. & Phillips, W. R. C. 2016 An asymptotic study of instability to Langmuir circulation in shallow layers. Geophys. Astrophys. Fluid Dyn. 110, 1–22.Google Scholar
Hayes, D. T. & Phillips, W. R. C. 2017 Nonlinear steady states to Langmuir circulation in shallow layers: an asymptotic study. Geophys. Astrophys. Fluid Dyn. 111, 65–90.Google Scholar
Herbert, T. 1983 On perturbation methods in nonlinear stability theory. J. Fluid Mech. 126, 167–186.Google Scholar
Holm, D. D. 1996 The ideal Craik–Leibovich equation. Physica D 98, 415–441.Google Scholar
Knobloch, E. & Luca, J. D. 1990 Amplitude equations for travelling wave convection. Nonlinearity 3, 975–980.Google Scholar
Langmuir, I. 1938 Surface motion of water induced by wind. Science 87, 119–123.Google Scholar
Leibovich, S. 1977 Convective instability of stably stratified water in the ocean. J. Fluid Mech. 82, 561–581.Google Scholar
Leibovich, S. 1980 On wave-current interaction theories of Langmuir circulations. J. Fluid Mech. 99, 715–724.Google Scholar
Leibovich, S. 1983 The form and dynamics of Langmuir circulations. Annu. Rev. Fluid Mech. 15, 391–427.Google Scholar
Leibovich, S.1997 Surface and near-surface motion of oil in the sea. Tech. Rep. Contract 14-35-0001-30612. Department of the Interior: Minerals Management Service.Google Scholar
Leibovich, S. & Paolucci, S. 1980 The Langmuir circulation instability as a mixing mechanism in the upper ocean. J. Phys. Oceanogr. 10, 186–207.Google Scholar
Leibovich, S. & Tandon, A. 1993 3-dimensional Langmuir circulation instability in a stratified layer. J. Geophys. Res. 98, 16501–16507.Google Scholar
Li, Q., Webb, A., Fox-Kemper, B., Craig, A., Danabasoglu, G., Large, W. G. & Vertenstein, M. 2016 Langmuir mixing effects on global climate: WAVEWATCH III in CESM. Ocean Model. 103, 145–160.Google Scholar
Longuet-Higgins, M. S. 1953 Mass transport in water waves. Phil. Trans. R. Soc. Lond. 245, 535–581.Google Scholar
Marmorino, G. O., Smith, G. B. & Lindemann, G. J. 2005 Infrared imagery of large-aspect-ratio Langmuir circulation. Cont. Shelf Res. 25, 1–6.Google Scholar
Maultsby, B. 2012 2:1 Spatial resonance in Langmuir circulation. In WHOI 2012 Program in Geophysical Fluid Dynamics (ed. Knobloch, E. & Weiss, J.) pp. 334–361. National Technical Information Service.Google Scholar
McWilliams, J. C., Sullivan, P. P. & Moeng, C.-H. 1997 Langmuir turbulence in the ocean. J. Fluid Mech. 334, 1–30.Google Scholar
Melville, W. K., Shear, R. & Veron, F. 1998 Laboratory measurements of the generation and evolution of Langmuir circulations. J. Fluid Mech. 364, 31–58.Google Scholar
Mizushima, J. 1993 Mechanism of mode selection in Rayleigh–Bénard convection with free rigid boundaries. Fluid Dyn. Res. 11, 297–311.Google Scholar
Mizushima, J. & Fujimura, K. 1992 Higher harmonic resonance of two-dimensional disturbances in Rayleigh–Bénard convection. J. Fluid Mech. 234, 651–667.Google Scholar
Moroz, I. M. & Leibovich, S. 1985 Oscillatory and competing instabilities in a nonlinear model for Langmuir circulations. Phys. Fluids (1958–1988) 28, 2050–2061.Google Scholar
Newell, A. C. & Whitehead, J. A. 1969 Finite bandwidth, finite amplitude convection. J. Fluid Mech. 38, 279–303.Google Scholar
Pearson, B., Fox-Kemper, B., Bachman, S. D. & Bryan, F. O. 2017 Evaluation of scale-aware subgrid mesoscale eddy models in a global eddy-rich model. Ocean Model. 115, 42–58.Google Scholar
Pham, K. G. & Suslov, S. A. 2018 On the definition of Landau constants in amplitude equations away from critical points. R. Soc. Open Sci. 5, 180746.Google Scholar
Phillips, W. R. C. 1998a Finite-amplitude rotational waves in viscous shear flows. Stud. Appl. Maths 101, 23–47.Google Scholar
Phillips, W. R. C. 1998b On the nonlinear instability of strong wavy shear to longitudinal vortices. In Nonlinear Instability, Chaos and Turbulence (ed. Debnath, L. & Riahi, D. N.), vol. 1, pp. 251–273. Comp. Mech. Publns.Google Scholar
Phillips, W. R. C. 2001 On an instability to Langmuir circulations and the role of Prandtl and Richardson numbers. J. Fluid Mech. 442, 335–358.Google Scholar
Phillips, W. R. C. 2002 Langmuir circulations beneath growing or decaying surface waves. J. Fluid Mech. 469, 317–342.Google Scholar
Phillips, W. R. C. 2015 Drift and pseudomomentum in bounded turbulent shear flows. Phys. Rev. E 92, 043003.Google Scholar
Phillips, W. R. C. & Dai, A. 2014 On Langmuir circulation in shallow waters. J. Fluid Mech. 743, 141–169.Google Scholar
Phillips, W. R. C., Dai, A. & Tjan, K. K. 2010 On Lagrangian drift in shallow-water waves on moderate shear. J. Fluid Mech. 660, 221–239.Google Scholar
Plueddemann, A., Smith, J., Farmer, D., Weller, R., Crawford, W., Pinkel, R., Vagle, S. & Gnanadesikan, A. 1996 Structure and variability of Langmuir circulation during the surface waves processes program. J. Geophys. Res. 21, 85–102.Google Scholar
Porter, J. & Knobloch, E. 2000 Complex dynamics in the 1:3 spatial resonance. Physica D 143, 138–168.Google Scholar
Porter, J. & Knobloch, E. 2001 New type of complex dynamics in the 1:2 spatial resonance. Physica D 159, 125–154.Google Scholar
Prat, J., Mercader, I. & Knobloch, E. 1998 Resonant mode interactions in Rayleigh–Bénard convection. Phys. Rev. E 58, 3145–3156.Google Scholar
Proctor, M. R. E. & Jones, C. A. 1988 The interaction of two spatially resonant patterns in thermal convection. Part 1. Exact 1:2 resonance. J. Fluid Mech. 188, 301–335.Google Scholar
Smith, J. A. 1992 Observed growth of Langmuir circulation. J. Geophys. Res. 97, 5651–5664.Google Scholar
Suslov, S. A. & Paolucci, S. 1997 Nonlinear analysis of convection flow in a tall vertical enclosure under non-Boussinesq conditions. J. Fluid Mech. 344, 1–41.Google Scholar
Suslov, S. A. & Paolucci, S. 2004 Stability of non-Boussinesq convection via the complex Ginzburg–Landau model. Fluid Dyn. Res. 35, 159–203.Google Scholar
Szeri, A. J. 1996 Langmuir circulations in Rodeo Lagoon. Mon. Weath. Rev. 124, 341–342.Google Scholar
Tandon, A. & Leibovich, S. 1995 Simulations of three-dimensional Langmuir circulation in water of constant density. J. Geophys. Res. 100, 22613–22623.Google Scholar
Thorpe, S. A. 2004 Langmuir circulation. Annu. Rev. Fluid Mech. 36, 55–79.Google Scholar
Tsai, W.-T., Chen, S.-M. & Lu, G.-H. 2015 Numerical evidence of turbulence generated by non-breaking surface waves. J. Phys. Oceanogr. 45, 174–180.Google Scholar
Tsai, W.-T., Chen, S.-M., Lu, G.-H. & Garbe, C. S. 2013 Characteristics of interfacial signatures on a wind-driven gravity-capillary wave. J. Geophys. Res. 118, 1715–1735.Google Scholar
Tsai, W. T., Lu, G. H., Chen, J. R., Dai, A. & Phillips, W. R. C. 2017 On the formation of coherent vortices beneath non-breaking free-propagating surface waves. J. Phys. Oceanogr. 47, 533–543.Google Scholar
Watson, J. 1960 On the non-linear mechanics of wave disturbances in stable and unstable parallel flows. Part 2. The development of a solution for plane Poiseuille flow and for plane Couette flow. J. Fluid Mech. 9, 371–389.Google Scholar
Zhang, Z., Chini, G. P., Julien, K. & Knobloch, E. 2015 Dynamic patterns in the reduced Craik–Leibovich equations. Phys. Fluids 27, 046605.Google Scholar