Published online by Cambridge University Press: 15 November 2011
In two previous papers (Wu, J. Fluid Mech., vol. 453, 2002, p. 289, and Wu & Hogg, J. Fluid Mech., vol. 550, 2006, p. 307), a formal asymptotic procedure was developed to calculate the sound radiated by unsteady boundary-layer flows that are described by the triple-deck theory. That approach requires lengthy calculations, and so is now improved to construct a simpler composite theory, which retains the capacity of systematically identifying and approximating the relevant sources, but also naturally includes the effect of mean-flow refraction and more importantly the back action of the emitted sound on the source itself. The combined effect of refraction and back action is represented by an ‘impedance coefficient’, and the present analysis yields an analytical expression for this parameter, which was usually introduced on a semi-empirical basis. The expression indicates that for Mach number 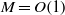 , the mean-flow refraction and back action of the sound have a leading-order effect on the acoustic field within the shallow angles to the streamwise directions. A parametric study suggests that the back effect of sound is actually appreciable in a sizeable portion of the acoustic field for
, the mean-flow refraction and back action of the sound have a leading-order effect on the acoustic field within the shallow angles to the streamwise directions. A parametric study suggests that the back effect of sound is actually appreciable in a sizeable portion of the acoustic field for 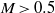 , becomes more pronounced, and eventually influences the entire acoustic field in the transonic limit. In the supersonic regime, the acoustic field is characterized by distinctive Mach-wave beams, which exert a leading-order influence on the source. The analysis also indicates that acoustic radiation in the subsonic and supersonic regimes is fundamentally different. In the subsonic regime, the sound is produced by small-wavenumber components of the hydrodynamic motion, and can be characterized by acoustic multipoles, whereas in the supersonic regime, broadband finite-wavenumber components of the hydrodynamic motion contribute and the concept of a multipolar source becomes untenable. The global acoustic feedback loop is investigated using a model consisting of two well-separated roughness elements, in which the sound wave emitted due to the scattering of a Tollmien–Schlichting (T–S) wave by the downstream roughness propagates upstream and impinges on the upstream roughness to regenerate the T–S wave. Numerical calculations suggest that at high Reynolds numbers and for moderate roughness heights, the long-range acoustic coupling may lead to global instability, which is characterized by self-sustained oscillations at discrete frequencies. The dominant peak frequency may jump from one value to another as the Reynolds number or the distance between the roughness elements is varied gradually.
, becomes more pronounced, and eventually influences the entire acoustic field in the transonic limit. In the supersonic regime, the acoustic field is characterized by distinctive Mach-wave beams, which exert a leading-order influence on the source. The analysis also indicates that acoustic radiation in the subsonic and supersonic regimes is fundamentally different. In the subsonic regime, the sound is produced by small-wavenumber components of the hydrodynamic motion, and can be characterized by acoustic multipoles, whereas in the supersonic regime, broadband finite-wavenumber components of the hydrodynamic motion contribute and the concept of a multipolar source becomes untenable. The global acoustic feedback loop is investigated using a model consisting of two well-separated roughness elements, in which the sound wave emitted due to the scattering of a Tollmien–Schlichting (T–S) wave by the downstream roughness propagates upstream and impinges on the upstream roughness to regenerate the T–S wave. Numerical calculations suggest that at high Reynolds numbers and for moderate roughness heights, the long-range acoustic coupling may lead to global instability, which is characterized by self-sustained oscillations at discrete frequencies. The dominant peak frequency may jump from one value to another as the Reynolds number or the distance between the roughness elements is varied gradually.