Article contents
Oblique collisions of internal wave beams and associated resonances
Published online by Cambridge University Press: 19 September 2012
Abstract
Quadratic nonlinear interactions between two colliding internal gravity wave beams in a uniformly stratified fluid, and the resulting radiation of secondary beams with frequencies equal to the sum and difference of those of the primary beams, are discussed. The analysis centres on oblique collisions, involving beams that propagate in different vertical planes. The propagation directions of generated secondary beams are deduced from kinematic considerations and the use of radiation conditions, thus extending to oblique collisions previously derived selection rules for plane collisions. Using small-amplitude expansions, radiated-beam profiles at steady state are also computed in terms of the characteristics of the colliding beams. It is pointed out that, for certain oblique collision configurations, radiated beams with frequency equal to the difference of the primary frequencies have unbounded steady-state amplitude. This resonance, which has no counterpart for plane collisions, is further analysed via the solution of an initial-value problem; ignoring dissipation, the transient resonant response grows in time like 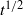 , a behaviour akin to that of forced waves at cut-off frequencies.
, a behaviour akin to that of forced waves at cut-off frequencies.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 4
- Cited by


