Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T04:55:24.789Z Has data issue: false hasContentIssue false
  • English
  • Français

A numerical study of turbulence under temporally evolving axisymmetric contraction and subsequent relaxation

Published online by Cambridge University Press:  22 September 2016

M. P. Clay  and
P. K. Yeung
M. P. Clay
Affiliation:
School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
P. K. Yeung*
Affiliation:
Schools of Aerospace Engineering and Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations using up to 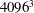$4096^{3}$ grid points on a deforming domain have been used to study the response of initially isotropic turbulence to a period of spatially uniform axisymmetric contraction (with one extensional and two equally compressive directions) and subsequent relaxation. A time-dependent strain rate is formulated to closely correspond to the downstream evolution in the wind tunnel experiments of Ayyalasomayajula & Warhaft (J. Fluid Mech., vol. 566, 2006, pp. 273–307), with a smoothly varying 4 : 1 contraction ratio. The application of strain leads to anisotropy in both the large scales and the small scales, in a manner where nonlinear effects not considered in rapid-distortion theory play an important role. Upon termination of strain, the small scales quickly return to isotropy while a residual level of anisotropy appears to persist at the large scales. The simulations are shown to reproduce many key findings from experiments, including distinctive changes in the form of the one-dimensional spectra in the extensional direction that arise at sufficiently high Reynolds number, during both the straining and relaxation periods. Scale-dependent measures of anisotropy are presented in terms of one-dimensional spectra and axisymmetric versions of the energy spectrum. To explain the observed changes in spectral shapes, various terms in the spectral evolution equation representing rapid pressure strain, slow pressure strain, production, nonlinear transfer and viscous dissipation are computed, showing that nonlinear effects take a dominant role when a wide range of scales exists. In particular, the ‘double-peak’ spectral form observed in experiments at high Reynolds number is found to be a consequence of the small scales relaxing towards isotropy much faster than the large scales. A comparison of results obtained from computational domains of varying sizes and grid resolutions show that the numerical findings are robust.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 805 , 25 October 2016 , pp. 460 - 493
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ayyalasomayajula, S. & Warhaft, Z. 2006 Nonlinear interactions in strained axisymmetric high-Reynolds-number turbulence. J. Fluid Mech. 566, 273–307.CrossRefGoogle Scholar
Batchelor, G. K. 1946 The theory of axisymmetric turbulence. Proc. R. Soc. Lond. A 186, 480–502.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K. & Proudman, I. 1954 The effect of rapid distortion of a fluid in turbulent motion. Q. J. Mech. Appl. Maths 7, 83–103.CrossRefGoogle Scholar
Brown, M. L., Parsheh, M. & Aidun, C. K. 2006 Turbulent flow in a converging channel: effect of contraction and return to isotropy. J. Fluid Mech. 560, 437–448.CrossRefGoogle Scholar
Chasnov, J. R. 1995 The decay of axisymmetric homogeneous turbulence. Phys. Fluids 7, 600–605.CrossRefGoogle Scholar
Chen, J., Meneveau, C. & Katz, J. 2006 Scale interactions of turbulence subjected to a straining-relaxation-destraining cycle. J. Fluid Mech. 562, 123–150.Google Scholar
Choi, K.-S. & Lumley, J. L. 2001 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 436, 59–84.CrossRefGoogle Scholar
Davidson, P. A., Okamoto, N. & Kaneda, Y. 2012 On freely decaying, anisotropic, axisymmetric Saffman turbulence. J. Fluid Mech. 706, 150–172.Google Scholar
Domaradzki, J. A. & Rogallo, R. S. 1990 Local energy transfer and nonlocal interactions in homogeneous, isotropic turbulence. Phys. Fluids A 2, 413–426.CrossRefGoogle Scholar
Donzis, D. A., Yeung, P. K. & Sreenivasan, K. R. 2008 Dissipation and enstrophy in isotropic turbulence: resolution effects and scaling in direct numerical simulations. Phys. Fluids 20, 045108.Google Scholar
Eswaran, V. & Pope, S. B. 1988 An examination of forcing in direct numerical simulations of turbulence. Comp. Fluids 16, 257–278.Google Scholar
Gence, J. N. & Mathieu, J. 1979 On the application of successive plane strains to grid-generated turbulence. J. Fluid Mech. 93, 501–513.Google Scholar
George, W. K. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.Google Scholar
Godeferd, F. S. & Staquet, C. 2003 Statistical modelling and direct numerical simulations of decaying stably stratified turbulence. Part 2. Large-scale and small-scale anisotropy. J. Fluid Mech. 486, 115–159.Google Scholar
Gotoh, T., Watanabe, Y., Shiga, Y., Nakano, T. & Suzuki, E. 2007 Statistical properties of four-dimensional turbulence. Phys. Rev. E 75, 016310.Google Scholar
Gualtieri, P. & Meneveau, C. 2010 Direct numerical simulations of turbulence subjected to a straining and destraining cycle. Phys. Fluids 22, 065104.Google Scholar
Gylfason, A. & Warhaft, Z. 2009 Effects of axisymmetric strain on a passive scalar field: modelling and experiment. J. Fluid Mech. 628, 339–356.Google Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Krogstad, P.-Å. & Davidson, P. A. 2010 Is grid turbulence Saffman turbulence? J. Fluid Mech. 642, 373–394.CrossRefGoogle Scholar
Lee, C.-M., Gylfason, Á., Perlekar, P. & Toschi, F. 2015 Inertial particle acceleration in strained turbulence. J. Fluid Mech. 785, 31–53.Google Scholar
Lee, M. J. & Reynolds, W. C.1985 Numerical experiments on the structure of homogeneous turbulence. Department of Mechanical Engineering, Stanford University, report TF-24.Google Scholar
Clark di Leoni, P., Cobelli, P. J., Mininni, P. D. & Dmitruk, P. 2014 Quantification of the strength of inertial waves in a rotating turbulent flow. Phys. Fluids 26, 035106.CrossRefGoogle Scholar
Liu, S., Katz, J. & Meneveau, C. 1999 Evolution and modelling of subgrid scales during rapid straining of turbulence. J. Fluid Mech. 387, 281–320.Google Scholar
Lumley, J. L. & Newman, G. R. 1977 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 82, 161–178.CrossRefGoogle Scholar
Mills, R. R. & Corrsin, S.1959 Effect of contraction on turbulence and temperature fluctuations generated by a warm grid. NASA Tech. Rep. 5-5-59W.Google Scholar
Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Isotropization at small scales of rotating helically driven turbulence. J. Fluid Mech. 699, 263–279.Google Scholar
Overholt, M. R. & Pope, S. B. 1996 Direct numerical simulation of a passive scalar with imposed mean gradient in isotropic turbulence. Phys. Fluids 8, 3128–3148.Google Scholar
Pearson, J. R. A. 1959 The effect of uniform distortion on weak homogeneous turbulence. J. Fluid Mech. 5, 274–288.CrossRefGoogle Scholar
Piessens, R., de Doncker-Kapenga, E., Überhuber, C. W. & Kahaner, D. K. 1983 QUADPACK: A Subroutine Package for Automatic Integration. Springer.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Reynolds, A. J. & Tucker, H. J. 1975 The distortion of turbulence by general uniform irrotational strain. J. Fluid Mech. 68, 673–693.Google Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence. NASA Tech. Memo. 81315. NASA Ames Research Center.Google Scholar
Rogers, M. M. & Moin, P. 1987 The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech. 176, 33–66.CrossRefGoogle Scholar
Saffman, P. G. 1967 The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 581–593.Google Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.Google Scholar
Sarkar, S. & Speziale, C. G. 1990 A simple nonlinear model for the return to isotropy in turbulence. Phys. Fluids A 2, 84–93.Google Scholar
Savill, A. M. 1987 Recent developments in rapid-distortion theory. Annu. Rev. Fluid Mech. 19, 531–575.Google Scholar
Sjögren, T. & Johansson, A. V. 1998 Measurement and modelling of homogeneous axisymmetric turbulence. J. Fluid Mech. 374, 59–90.CrossRefGoogle Scholar
Speziale, C. G. 1991 Analytical methods for the development of Reynolds-stress closures in turbulence. Annu. Rev. Fluid Mech. 23, 107–157.Google Scholar
Tavoularis, S., Bennett, J. C. & Corrsin, S. 1978 Velocity-derivative skewness in small Reynolds number, nearly isotropic turbulence. J. Fluid Mech. 88, 63–69.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Uberoi, M. 1956 Effect of wind-tunnel contraction on free-stream turbulence. J. Aero. Sci. 23, 754–764.Google Scholar
Warhaft, Z. 1980 An experimental study of the effect of uniform strain on thermal fluctuations in grid-generated turbulence. J. Fluid Mech. 99, 545–573.CrossRefGoogle Scholar
Warhaft, Z. 2009 Why we need experiments at high Reynolds numbers. Fluid Dyn. Res. 41, 021401.CrossRefGoogle Scholar
Yeung, P. K., Brasseur, J. G. & Wang, Q. 1995 Dynamics of direct large-small scale couplings in coherently forced turbulence: concurrent physical- and Fourier-space views. J. Fluid Mech. 283, 43–95.Google Scholar
Yeung, P. K. & Zhou, Y. 1997 Universality of the Kolmogorov constant in numerical simulations of turbulence. Phys. Rev. E 56, 1746–1752.Google Scholar
Zusi, C. J. & Perot, J. B. 2013 Simulation and modeling of turbulence subjected to a period of uniform plane strain. Phys. Fluids 25, 110819.Google Scholar
Zusi, C. J. & Perot, J. B. 2014 Simulation and modeling of turbulence subjected to a period of axisymmetric contraction or expansion. Phys. Fluids 26, 115103.Google Scholar