Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-11T22:47:08.780Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical study of rotational diffusion in sheared semidilute fibre suspension

Published online by Cambridge University Press:  21 December 2011

Asif Salahuddin ,
Jingshu Wu  and
C. K. Aidun
Asif Salahuddin
Affiliation:
Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30318, USA
Jingshu Wu
Affiliation:
Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30318, USA
C. K. Aidun*
Affiliation:
Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30318, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Fibre-level computer simulation is carried out to study the rotational diffusion and structural evolution of semidilute suspensions of non-Brownian, rigid-rod-like fibres under shear flow in a Newtonian fluid. The analyses use a hybrid approach where the lattice-Boltzmann method is coupled with the external boundary force method. The probability distribution of the orbit constant, 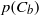, in the semidilute regime is predicted with this method. The paper emphasizes assessment of the characteristics of a rotary diffusion model – anisotropic in nature (Koch, Phys. Fluids, vol. 7, 1995, pp. 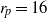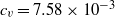2086–2088) – when used in suspensions with fibres of different aspect ratios (ranging from to ) and with different volume concentrations (ranging from to 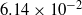). A measure of the scalar Folgar–Tucker constant, 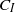, is extracted from the anisotropic diffusivity tensor, 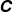. The scalar 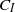is mostly 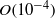in the semidilute regime and compares very well with the experimental observations of Stover (PhD thesis, School of Chemical Engineering, Cornell University, 1991) and Stover, Koch & Cohen (J. Fluid Mech., vol. 238, 1992, pp. 277–296). The 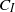values provide substantial numerical evidence that the range of 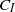(0.0038–0.0165) obtained by Folgar & Tucker (J. Rein. Plast. Compos., vol. 3, 1984, pp. 98–119) in the semidilute regime is actually overly diffusive. The paper also branches out to incorporate anisotropic diffusion (through the use of the Koch model) in the second-order evolution equation for 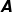(a second-order orientation tensor). The solution of the evolution equation with the Koch model demonstrates unphysical behaviour at low concentrations. The most plausible explanation for this behaviour is error in the closure approximation; and the use of the Koch model in a spherical harmonics-based method (Montgomery-Smith, Jack & Smith, Compos. A: Appl. Sci. Manuf., vol. 41, 2010, pp. 827–835) to solve for the orientation moments corroborates this claim.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 692 , 10 February 2012 , pp. 153 - 182
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Advani, S. G. & Tucker, C. L. III 1987 The use of tensors to describe and predict fiber orientation in short fiber composites. J. Rheol. 31 (8), 751–784.CrossRefGoogle Scholar
2.Advani, S. G. & Tucker, C. L. III 1990 Closure approximations for three-dimensional structure tensors. J. Rheol. 34 (3), 367–386.CrossRefGoogle Scholar
3.Aidun, C. K., Lu, Y. & Ding, E. J. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287.CrossRefGoogle Scholar
4.Anczurowski, E. & Mason, S. G. 1967a The kinetics of flowing dispersions: II. Equilibrium orientations of rods and discs (theoretical). J. Colloid Interface Sci. 23 (4), 522–532.CrossRefGoogle Scholar
5.Anczurowski, E. & Mason, S. G. 1967b The kinetics of flowing dispersions: III. Equilibrium orientations of rods and discs (experimental). J. Colloid Interface Sci. 23 (4), 533–546.CrossRefGoogle Scholar
6.Bay, R. S. 1991 Fiber orientation in injection molded composites: a comparison of theory and experiment. PhD thesis, University of Illinois, Urbana–Champaign.Google Scholar
7.Bay, R. S. & Tucker, C. L. III 1992a Fiber orientation in simple injection moldings. Part I. Theory and numerical methods. Polym. Compos. 13 (04), 317–331.CrossRefGoogle Scholar
8.Bay, R. S. & Tucker, C. L. III 1992b Fiber orientation in simple injection moldings. Part II. Experimental results. Polym. Compos. 13 (04), 332–341.CrossRefGoogle Scholar
9.Chen, H., Chen, S. & Matthaeus, W. H. 1992 Recovery of the Navier–Stokes equations using a lattice-gas Boltzmann method. Phys. Rev. A 45, 5339.CrossRefGoogle ScholarPubMed
10.Chung, D. H. & Kwon, T. H. 2002 Fiber orientation in the processing of polymer composites. Korea–Aust. Rheol. J. 14, 175–188.Google Scholar
11.Cintra, J. S. Jr. & Tucker, C. L. III 1995 Orthotropic closure approximations for flow-induced fiber orientation. J. Rheol. 39 (6), 1095–1122.CrossRefGoogle Scholar
12.Cox, R. G. 1971 The motion of long slender bodies in a viscous fluid. Part 2. Shear flow. J. Fluid Mech. 45 (04), 625–657.CrossRefGoogle Scholar
13.Ding, E. J. & Aidun, C. K. 2003 Extension of the lattice-Boltzmann method for direct simulation of suspended particles near contact. J. Stat. Phys. 112 (3/4), 685–708.CrossRefGoogle Scholar
14.Dupret, F. & Verleye, V. 1999 Modelling the Flow of Fiber Suspensions in Narrow Gaps, Rheology Series , pp. 1347–1398. Elsevier.Google Scholar
15.Ericksen, J. L. 1960 Anisotropic fluids. Arch. Rat. Mech. Anal. 4, 231–237.CrossRefGoogle Scholar
16.Evans, K. E. & Gibson, A. G. 1986 Prediction of the maximum packing fraction achievable in randomly oriented short-fiber composites. Compos. Sci. Technol. 25 (2), 149–162.CrossRefGoogle Scholar
17.Fan, X.-J., Phan-Thien, N. & Zheng, R. 1998 A direct simulation of fiber suspensions. J. Non-Newtonian Fluid Mech. 74 (1–3), 113–135.CrossRefGoogle Scholar
18.Feng, Z. & Michaelides, E. 2004 The immersed boundary–lattice Boltzmann method for solving fluid–particles interaction problems. J. Comput. Phys. 195, 602–628.CrossRefGoogle Scholar
19.Folgar, F. & Tucker, C. L. III 1984 Orientation behaviour of fibers in concentrated suspensions. J. Rein. Plast. Compos. 3 (2), 98–119.CrossRefGoogle Scholar
20.Goldstein, D., Handler, R. & Sirovich, L. 1993 Modelling a no-slip flow boundary with an external force field. J. Comput. Phys. 105 (2), 354–366.CrossRefGoogle Scholar
21.Hand, G. L. 1961 A theory of dilute suspensions. Arch. Rat. Mech. Anal. 7, 81–86.CrossRefGoogle Scholar
22.Hinch, E. J. & Leal, L. G. 1972 The effect of Brownian motion on the rheological properties of a suspension of non-spherical particles. J. Fluid Mech. 52 (04), 683–712.CrossRefGoogle Scholar
23.Hinch, E. J. & Leal, L. G. 1973 Time-dependent shear flows of a suspension of particles with weak Brownian rotations. J. Fluid Mech. 57 (04), 753–767.CrossRefGoogle Scholar
24.Hou, S., Zou, Q., Chen, S., Doolen, G. & Cogley, A. C. 1995 Simulation of cavity flow by lattice Boltzmann method. J. Comput. Phys. 118, 329.CrossRefGoogle Scholar
25.Ivanov, Y. & van de Ven, T. G. M. 1982 Damped oscillations in the viscosity of suspensions of rigid rods. II. Bimodal and polydisperse suspensions. J. Rheol. 26, 231–244.CrossRefGoogle Scholar
26.Ivanov, Y., van de Ven, T. G. M. & Mason, S. G. 1982 Damped oscillations in the viscosity of suspensions of rigid rods. I. Monomodal suspensions. J. Rheol. 26, 213–230.CrossRefGoogle Scholar
27.Jack, D. A. & Smith, D. E. 2005 An invariant based fitted closure of the sixth-order orientation tensor for modelling short-fiber suspensions. J. Rheol. 49 (5), 1091–1115.CrossRefGoogle Scholar
28.Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. Ser. A 102 (715), 161–179.Google Scholar
29.Joung, C. G., Phan-Thien, N. & Fan, X.-J. 2001 Direct simulation of flexible fibers. J. Non-Newtonian Fluid Mech. 99 (1), 1–36.CrossRefGoogle Scholar
30.Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
31.Koch, D. L. 1989 On hydrodynamic diffusion and drift in sheared suspensions. Phys. Fluids A: Fluid Dyn. 1 (10), 1742–1745.CrossRefGoogle Scholar
32.Koch, D. L. 1995 A model for orientational diffusion in fiber suspensions. Phys. Fluids 7 (8), 2086–2088.CrossRefGoogle Scholar
33.Krochak, P. J., Olson, J. A. & Martinez, D. M. 2008 The orientation of semidilute rigid fiber suspensions in a linearly contracting channel. Phys. Fluids 20 (7), 073303.CrossRefGoogle Scholar
34.Leal, L. G. & Hinch, E. J. 1971 The effect of weak Brownian rotations on particles in shear flow. J. Fluid Mech. 46 (04), 685–703.CrossRefGoogle Scholar
35.Lindström, S. B. & Uesaka, T. 2008 Simulation of semidilute suspensions of non-Brownian fibers in shear flow. J. Chem. Phys. 128 (2), 024901.CrossRefGoogle ScholarPubMed
36.Lindström, S. B. & Uesaka, T. 2009 A numerical investigation of the rheology of sheared fiber suspensions. Phys. Fluids 21 (8), 083301.CrossRefGoogle Scholar
37.MacMeccan, R. M., Clausen, J. R., Neitzel, G. P. & Aidun, C. K. 2009 Simulating deformable particle suspensions using a coupled lattice-Boltzmann and finite-element method. J. Fluid Mech. 618, 13–39.CrossRefGoogle Scholar
38.McNamara, G. R. & Zanetti, G. 1988 Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 61, 2332.CrossRefGoogle ScholarPubMed
39.Montgomery-Smith, S., Jack, D. A. & Smith, D. E. 2010 A systematic approach to obtaining numerical solutions of Jeffery’s type equations using spherical harmonics. Compos. A: Appl. Sci. Manuf. 41 (7), 827–835.CrossRefGoogle Scholar
40.Okagawa, A., Cox, R. G. & Mason, S. G. 1973 The kinetics of flowing dispersions. VI. Transient orientation and rheological phenomena of rods and discs in shear flow. J. Colloid Interface Sci. 45 (2), 303–329.CrossRefGoogle Scholar
41.Olson, J. A., Frigaard, I., Chan, C. & Hämäläinen, J. P. 2004 Modelling a turbulent fiber suspension flowing in a planar contraction: the one-dimensional headbox. Intl J. Multiphase Flow 30 (1), 51–66.CrossRefGoogle Scholar
42.Parsheh, M., Brown, M. L. & Aidun, C. K. 2005 On the orientation of stiff fibers suspended in turbulent flow in a planar contraction. J. Fluid Mech. 545, 245–269.CrossRefGoogle Scholar
43.Peskin, C. S. 1977 Numerical analysis of blood flow in the heart. J. Comput. Phys. 25, 220–252.CrossRefGoogle Scholar
44.Petrich, M. P., Koch, D. L. & Cohen, C. 2000 An experimental determination of the stress–microstructure relationship in semi-concentrated fiber suspensions. J. Non-Newtonian Fluid Mech. 95 (2–3), 101–133.CrossRefGoogle Scholar
45.Phan-Thien, N., Fan, X.-J., Tanner, R. I. & Zheng, R. 2002 Folgar–Tucker constant for a fiber suspension in a Newtonian fluid. J. Non-Newtonian Fluid Mech. 103 (2–3), 251–260.CrossRefGoogle Scholar
46.Phan-Thien, N. & Kim, S. 1994 Microstructure in Elastic Media: Principles and Computational Methods. Oxford University Press.CrossRefGoogle Scholar
47.Phelps, J. H. 2009 Processing microstructure models for short- and long-fiber thermoplastic composites. PhD thesis, Mechanical Engineering, University of Illinois at Urbana-Champaign.Google Scholar
48.Phelps, J. H. & Tucker, C. L. III 2009 An anisotropic rotary diffusion model for fiber orientation in short- and long-fiber thermoplastics. J. Non-Newtonian Fluid Mech. 156 (3), 165–176.CrossRefGoogle Scholar
49.Rahnama, M., Koch, D. L. & Shaqfeh, E. S. G. 1995 The effect of hydrodynamic interactions on the orientation distribution in a fiber suspension subject to simple shear flow. Phys. Fluids 7 (3), 487–506.CrossRefGoogle Scholar
50.Shaqfeh, E. S. G. & Koch, D. L. 1988 The effect of hydrodynamic interactions on the orientation of axisymmetric particles flowing through a fixed bed of spheres or fibers. Phys. Fluids 31 (4), 728–744.CrossRefGoogle Scholar
51.Shaqfeh, E. S. G. & Koch, D. L. 1990 Orientational dispersion of fibers in extensional flows. Phys. Fluids A: Fluid Dyn. 2 (7), 1077–1094.CrossRefGoogle Scholar
52.Stover, C. A. 1991 The dynamics of fibers suspended in shear flow. PhD thesis, School of Chemical Engineering, Cornell University.Google Scholar
53.Stover, C. A. & Cohen, C. 1990 The motion of rodlike particles in the pressure-driven flow between two flat plates. Rheol. Acta 29, 192–203.CrossRefGoogle Scholar
54.Stover, C. A., Koch, D. L. & Cohen, C. 1992 Observations of fiber orientation in simple shear flow of semi-dilute suspensions. J. Fluid Mech. 238, 277–296.CrossRefGoogle Scholar
55.Sundararajakumar, R. R. & Koch, D. L. 1997 Structure and properties of sheared fiber suspensions with mechanical contacts. J. Non-Newtonian Fluid Mech. 73 (3), 205–239.CrossRefGoogle Scholar
56.Switzer, L. H. III & Klingenberg, D. J. 2003 Rheology of sheared flexible fiber suspensions via fiber-level simulations. J. Rheol. 47 (3), 759–778.CrossRefGoogle Scholar
57.Tucker, C. L. III & Advani, S. G. 1994 Processing of Short-fiber Systems, Composite Materials Series , vol. 10. Elsevier.Google Scholar
58.Wu, J. & Aidun, C. K. 2010a A method for direct simulation of flexible fiber suspensions using lattice-Boltzmann equation with external boundary force. Intl J. Multiphase Flow 36, 202–209.CrossRefGoogle Scholar
59.Wu, J. & Aidun, C. K. 2010b A numerical study of the effect of fiber stiffness on the rheology of sheared flexible fiber suspensions. J. Fluid Mech. 662, 123–133.CrossRefGoogle Scholar
60.Wu, J. & Aidun, C. K. 2010c Simulating 3D deformable particle suspensions using lattice Boltzmann method with discrete external boundary force. Intl J. Numer. Meth. Fluids 62, 765–783.CrossRefGoogle Scholar
61.Yamane, Y., Kaneda, Y. & Dio, M. 1994 Numerical simulation of semi-dilute suspensions of rodlike particles in shear flow. J. Non-Newtonian Fluid Mech. 54, 405–421.CrossRefGoogle Scholar
62.Zuzovsky, M., Priel, Z. & Mason, S. G. 1980 Memory impairment in flowing suspensions. III. Brownian rotation of spheroids. J. Colloid Interface Sci. 75 (1), 230–239.CrossRefGoogle Scholar