Published online by Cambridge University Press: 20 February 2015
Large-eddy simulations are conducted to uncover physical aspects of sidewall-induced three-dimensionality for a moderately separated oblique shock-wave/boundary-layer interaction (SWBLI) at 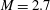 $M=2.7$. Simulations are run for three different aspect ratios of the interaction zone. The swept SWBLI on the sidewalls and the corner flow behaviour are investigated, along with the main oblique SWBLI on the bottom wall. As the aspect ratio decreases to unity, the separation and reattachment points on the central plane are observed to move upstream simultaneously, while the bubble length initially increases and then stabilizes to a length 30 % larger than for the infinite-span quasi-two-dimensional case. A distorted incident shock and a three-dimensional (3D) bottom-wall separation pattern are observed, with a patch of attached flow between the central and corner separations. The 3D flow structure is found to be induced by the swept SWBLI formed on the sidewalls. The location of the termination point of the incident shock near the sidewall is limited by a sweepback effect, allowing the definition of a penetration Mach number
$M=2.7$. Simulations are run for three different aspect ratios of the interaction zone. The swept SWBLI on the sidewalls and the corner flow behaviour are investigated, along with the main oblique SWBLI on the bottom wall. As the aspect ratio decreases to unity, the separation and reattachment points on the central plane are observed to move upstream simultaneously, while the bubble length initially increases and then stabilizes to a length 30 % larger than for the infinite-span quasi-two-dimensional case. A distorted incident shock and a three-dimensional (3D) bottom-wall separation pattern are observed, with a patch of attached flow between the central and corner separations. The 3D flow structure is found to be induced by the swept SWBLI formed on the sidewalls. The location of the termination point of the incident shock near the sidewall is limited by a sweepback effect, allowing the definition of a penetration Mach number 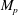 $M_{p}$ that is shown to correlate well with the spanwise extent of the core flow. The structure and strength of the incident shock are modified significantly by the swept SWBLI on the sidewalls, along with a compression wave upstream and a secondary sidewall shock downstream, leading to a highly 3D pressure field in the main flow above the main SWBLI on the bottom wall. The reflection of the swept SWBLI from the bottom wall leads to a corner compression wave and strong transverse flow close to the bottom wall. A physical model based on the quasi-conical structure of the swept SWBLI on the sidewall is proposed to estimate the 3D SWBLI pattern on the bottom wall, in which the swept SWBLI features and the aspect ratio of the interaction zone are considered to be the critical factors.
$M_{p}$ that is shown to correlate well with the spanwise extent of the core flow. The structure and strength of the incident shock are modified significantly by the swept SWBLI on the sidewalls, along with a compression wave upstream and a secondary sidewall shock downstream, leading to a highly 3D pressure field in the main flow above the main SWBLI on the bottom wall. The reflection of the swept SWBLI from the bottom wall leads to a corner compression wave and strong transverse flow close to the bottom wall. A physical model based on the quasi-conical structure of the swept SWBLI on the sidewall is proposed to estimate the 3D SWBLI pattern on the bottom wall, in which the swept SWBLI features and the aspect ratio of the interaction zone are considered to be the critical factors.