Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-03T19:51:02.878Z Has data issue: false hasContentIssue false
  • English
  • Français

A numerical study of a weakly stratified turbulent wake

Published online by Cambridge University Press:  13 July 2015

J. A. Redford ,
T. S. Lund  and
G. N. Coleman
J. A. Redford
Affiliation:
Aerodynamics and Flight Mechanics, University of Southampton, Highfield, Southampton SO17 1BJ, UK
T. S. Lund
Affiliation:
NorthWest Research Associates – CORA Division, Colorado Research Associates, 3380 Mitchell Lane, Boulder, CO 80301, USA
G. N. Coleman*
Affiliation:
Computational AeroSciences, NASA Langley Research Center, Hampton, VA 23681, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation (DNS) of a time-developing turbulent wake evolving in a stably stratified background is presented. A large initial Froude number is chosen to allow the wake to become fully turbulent and axisymmetric before stratification affects the spreading rate of the mean defect. Turbulence statistics are formed by averaging over the homogeneous streamwise direction of a domain that is larger than earlier stratified-wake simulations in order to reduce the statistical uncertainty. The DNS results are used to cast light on the mechanisms that lead to the various states of this flow – namely the three-dimensional (essentially unstratified), non-equilibrium (or ‘wake-collapse’) and quasi-two-dimensional (or ‘two-component’) regimes, previously observed for wakes embedded in both weakly and strongly stratified backgrounds. For this relatively high-initial-Reynolds- and Froude-number simulation, we find that the signature reduction in the rate of decay of the maximum mean defect velocity during the wake-collapse regime is due to buoyancy-induced alterations of the turbulence structure, which weaken and redistribute the Reynolds shear stresses whose gradients appear in the streamwise mean momentum equation. The change in the rate of decay of the turbulence kinetic energy (TKE) observed during the wake-collapse regime (which occurs well after the mean velocity decay reduction begins) is not caused by transfer of turbulent gravitational potential energy to TKE, as has been previously suggested. The results instead reveal that the reduction in TKE decay – which for this flow, with its relatively weak internal waves, eventually leads to TKE growth, heralding the arrival of the two-component regime – is caused by an increase in the rate of TKE production associated with the wake structure becoming increasingly two-dimensional, such that the lateral Reynolds shear stress, 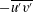$-\overline{u^{\prime }v^{\prime }}$, becomes dominant. The present results are also compared with those of previous simulations at different Froude and Reynolds numbers, and whose initial conditions contain different turbulence structures. This comparison confirms a strong degree  of commonality in the late-wake behaviour, which lends support to the hypothesis that all wakes in stably stratified environments achieve a universal state in the final stages of decay.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulence simulation Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 568 - 609
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: CMLA, ENS de Cachan, 61 avenue du président Wilson, 94235 Cachan, France.

References

Abdilghanie, A. M. & Diamessis, P. J. 2013 The internal gravity wave field emitted by a stably stratified turbulent wake. J. Fluid Mech. 720, 104–139.CrossRefGoogle Scholar
Bevilaqua, P. M. & Lykoudis, P. S. 1978 Turbulence memory in self-preserving wakes. J. Fluid Mech. 89 (3), 589–606.Google Scholar
Bonnier, M., Bonneton, P. & Eiff, O. 1998 Far-wake of a sphere in a stably stratified fluid. Appl. Sci. Res. 59, 269–281.Google Scholar
Bonnier, M. & Eiff, O. 2002 Experimental investigation of the collapse of a turbulent wake in a stably stratified fluid. Phys. Fluids 14, 793–801.Google Scholar
Bradshaw, P. 1988 Effects of extra rates of strain – review. In Zoran Zaric Mem. Seminar, Dubrovnik. Hemisphere.Google Scholar
Brucker, K. A. & Sarkar, S. 2010 A comparative study of self-propelled and towed wakes in a stratified fluid. J. Fluid Mech. 652, 373–404.Google Scholar
Chomaz, J. M., Bonneton, P., Butet, A. & Hopfinger, E. J. 1993 Vertical diffusion of the far wake of a sphere moving in a stratified fluid. Phys. Fluids 5 (11), 2799–2806.Google Scholar
Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1992 Direct simulation of the stably stratified turbulent Ekman layer. J. Fluid Mech. 244, 677–712; Corrigendum: 252, 721.CrossRefGoogle Scholar
Diamessis, P. J., Spedding, G. R. & Domaradzki, J. A. 2011 Similarity scaling and vorticity structure in high-Reynolds-number stably stratified turbulent wakes. J. Fluid Mech. 671, 52–95.Google Scholar
Dommermuth, D. G., Rottman, J. W., Innis, G. E. & Novikov, E. A. 2002 Numerical simulation of the wake of a towed sphere in a weakly stratified fluid. J. Fluid Mech. 473, 83–101.Google Scholar
Godeford, F. S. & Cambon, C. 1994 Detailed investigation of energy transfer in homogeneous stratified turbulence. Phys. Fluids 6 (6), 2084–2100.CrossRefGoogle Scholar
Gottlieb, D. & Orszag, S. A. 1977 Numerical Analysis of Spectral Methods: Theory and Applications. SIAM.CrossRefGoogle Scholar
Gourlay, M. J., Arendt, S. C., Fritts, D. C. & Werne, J. 2001 Numerical modeling of initially turbulent wakes with net momentum. Phys. Fluids 13 (12), 3783–3802.Google Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006 Predicting turbulence in flows with strong stable stratification. Phys. Fluids 18, 066602.Google Scholar
Itsweire, E. C., Koseff, J. R., Briggs, D. A. & Ferziger, J. H. 1993 Turbulence in stratified shear flows: implications for interpreting shear-induced mixing in the ocean. J. Phys. Oceanogr. 23, 1508–1522.Google Scholar
Ivey, G. N. & Imberger, J. 1991 On the nature of turbulence in a stratified fluid: Part I. The energetics of mixing. J. Phys. Oceanogr. 21, 301–320.Google Scholar
Johansson, P. B. V., George, W. K. & Gourlay, M. J. 2003 Equilibrium similarity, effects of initial conditions and local Reynolds number on the axisymmetric wake. Phys. Fluids 15 (3), 603–617.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kundu, P. K. 1990 Fluid Mechanics. Academic.Google Scholar
Lin, J. T. & Pao, Y. H. 1979 Wakes in stratified fluids. Annu. Rev. Fluid Mech. 11, 317–338.Google Scholar
Meunier, P., Diamessis, P. J. & Spedding, G. R. 2006 Self-preservation in stratified momentum wakes. Phys. Fluids 18, 106601.Google Scholar
Meunier, P. & Spedding, G. R. 2004 A loss of memory in stratified momentum wakes. Phys. Fluids 16, 298–305.Google Scholar
Nedic, J., Vassilicos, J. C. & Ganapathisubramani, B. 2013 Axisymmetric turbulent wakes with new nonequilibrium similarity scalings. Phys. Rev. Lett. 111, 144503.Google Scholar
Pal, A., de Stadler, M. B. & Sarkar, S. 2013 The spatial evolution of fluctuations in a self-propelled wake compared to a patch of turbulence. Phys. Fluids 25, 095106.CrossRefGoogle Scholar
Redford, J. A., Castro, I. P. & Coleman, G. N. 2012 On the universality of turbulent axisymmetric wakes. J. Fluid Mech. 710, 419–452; (referred to herein as RCC).Google Scholar
Redford, J. A., Lund, T. S. & Coleman, G. N.2014 Direct numerical simulation of a weakly stratified turbulent wake. NASA TM-2014-218523. Available from NASA Scientific & Technical Information (www.sti.nasa.gov; ).Google Scholar
Riley, J. J. & Lelong, M.-P. 2000 Fluid motions in the presence of strong stratification. Annu. Rev. Fluid Mech. 32, 613–657.Google Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence. NASA TM 81315. NASA Ames Research Center.Google Scholar
Shariff, K., Verzicco, R. & Orlandi, P. 1994 Three-dimensional vortex ring instabilities. J. Fluid Mech. 279, 351–375.CrossRefGoogle Scholar
Spalart, P. E., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96 (2), 297–324.Google Scholar
Spedding, G. R. 1997 The evolution of initially turbulent bluff-body wakes at high internal Froude number. J. Fluid Mech. 337, 283–301.Google Scholar
Spedding, G. R. 2001 Anisotropy in turbulence profiles of stratified wakes. Phys. Fluids 13, 2361–2372.CrossRefGoogle Scholar
Spedding, G. R. 2002 Vertical structure in stratified wakes with high initial Froude number. J. Fluid Mech. 454, 71–112.Google Scholar
Spedding, G. R., Browand, F. K. & Fincham, A. M. 1996 Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluid. J. Fluid Mech. 314, 53–103.CrossRefGoogle Scholar
de Stadler, M. B., Rapaka, N. R. & Sarkar, S. 2014 Large eddy simulation of the near to intermediate wake of a heated sphere at $\mathit{Re}=10\,000$ . Intl J. Heat Fluid Flow 49, 2–10.Google Scholar
de Stadler, M. B. & Sarkar, S. 2012 Simulation of a propelled wake with moderate excess momentum in a stratified fluid. J. Fluid Mech. 692, 28–52.Google Scholar
de Stadler, M. B., Sarkar, S. & Brucker, K. A. 2010 Effect of Prandtl number on a stratified turbulent wake. Phys. Fluids 22, doi:10.1063/1.3478841.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Uberoi, M. S. & Freymuth, P. 1970 Turbulent energy balance and spectra of the axisymmetric wake. Phys. Fluids 13 (9), 2205–2210.Google Scholar