Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-01T06:48:01.642Z Has data issue: false hasContentIssue false
  • English
  • Français

A numerical study of a variable-density low-speed turbulent mixing layer

Published online by Cambridge University Press:  02 October 2017

Antonio Almagro Open the ORCID record for Antonio Almagro [Opens in a new window] ,
Manuel García-Villalba Open the ORCID record for Manuel García-Villalba [Opens in a new window]  and
Oscar Flores Open the ORCID record for Oscar Flores [Opens in a new window]
Antonio Almagro*
Affiliation:
Departamento de Bioingeniería e Ingeniería Aeroespacial, Universidad Carlos III de Madrid, 28911 Leganés, Spain
Manuel García-Villalba
Affiliation:
Departamento de Bioingeniería e Ingeniería Aeroespacial, Universidad Carlos III de Madrid, 28911 Leganés, Spain
Oscar Flores
Affiliation:
Departamento de Bioingeniería e Ingeniería Aeroespacial, Universidad Carlos III de Madrid, 28911 Leganés, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations of a temporally developing, low-speed, variable-density, turbulent, plane mixing layer are performed. The Navier–Stokes equations in the low-Mach-number approximation are solved using a novel algorithm based on an extended version of the velocity–vorticity formulation used by Kim et al. (J. Fluid Mech., vol 177, 1987, 133–166) for incompressible flows. Four cases with density ratios 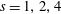$s=1,2,4$ and 8 are considered. The simulations are run with a Prandtl number of 0.7, and achieve a 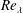$Re_{\unicode[STIX]{x1D706}}$ up to 150 during the self-similar evolution of the mixing layer. It is found that the growth rate of the mixing layer decreases with increasing density ratio, in agreement with theoretical models of this phenomenon. Comparison with high-speed data shows that the reduction of the growth rates with increasing density ratio has a weak dependence with the Mach number. In addition, the shifting of the mixing layer to the low-density stream has been characterized by analysing one-point statistics within the self-similar interval. This shifting has been quantified, and related to the growth rate of the mixing layer under the assumption that the shape of the mean velocity and density profiles do not change with the density ratio. This leads to a predictive model for the reduction of the growth rate of the momentum thickness, which agrees reasonably well with the available data. Finally, the effect of the density ratio on the turbulent structure has been analysed using flow visualizations and spectra. It is found that with increasing density ratio the longest scales in the high-density side are gradually inhibited. A gradual reduction of the energy in small scales with increasing density ratio is also observed.

JFM classification

Turbulent Flows: Shear layer turbulence Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 830 , 10 November 2017 , pp. 569 - 601
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashurst, W. T. & Kerstein, A. R. 2005 One-dimensional turbulence: variable-density formulation and application to mixing layers. Phys. Fluids 17, 025107.Google Scholar
Bell, J. H. & Mehta, R. D. 1990 Development of a two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28 (12), 2034–2042.Google Scholar
Bogdanoff, D. W. 1983 Compressibility effects in turbulent shear layers. AIAA J. 21 (6), 926–927.Google Scholar
Bretonnet, L., Cazalbou, J.-B., Chassaing, P. & Braza, M. 2007 Deflection, drift, and advective growth in variable-density, laminar mixing layers. Phys. Fluids 19 (10), 103601.Google Scholar
Brown, G. L. 1974 The entrainment and large structure in turbulent mixing layers. In Proceedings of the 5th Australasian Conference on Hydraulics and Fluid Mechanics, pp. 352–359.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.Google Scholar
Carlier, J. & Sodjavi, K. 2016 Turbulent mixing and entrainment in a stratified horizontal plane shear layer: joint velocity-temperature analysis of experimental data. J. Fluid Mech. 806, 542–579.CrossRefGoogle Scholar
Chassaing, P., Antonia, R. A., Anselmet, F., Joly, L. & Sarkar, S. 2002 Variable Density Fluid Turbulence. Springer.Google Scholar
Clemens, N. T. & Mungal, M. G. 1992 Two-and three-dimensional effects in the supersonic mixing layer. AIAA J. 30 (4), 973–981.Google Scholar
Cook, A. W. & Riley, J. J. 1996 Direct numerical simulation of a turbulent reactive plume on a parallel computer. J. Comput. Phys. 129 (2), 263–283.Google Scholar
Dimotakis, P. E. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24 (11), 1791–1796.Google Scholar
Dimotakis, P. E. 1991 Turbulent free shear layer mixing and combustion. High Speed Flight Propulsion Systems 137, 265–340.Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37 (1), 329–356.Google Scholar
Driscoll, T. A, Bornemann, F. & Trefethen, L. N 2008 The chebop system for automatic solution of differential equations. BIT Num. Math. 48 (4), 701–723.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.Google Scholar
Fontane, J. & Joly, L. 2008 The stability of the variable-density Kelvin–Helmholtz billow. J. Fluid Mech. 612, 237–260.Google Scholar
Gatski, T. B. & Bonnet, J.-P. 2013 Compressibility, Turbulence and High Speed Flow. Academic.Google Scholar
Hall, J. L., Dimotakis, P. E. & Rosemann, H. 1993 Experiments in nonreacting compressible shear layers. AIAA J. 31 (12), 2247–2254.Google Scholar
Higuera, F. J. & Moser, R. D. 1994 Effect of chemical heat release in a temporally evolving mixing layer. CTR Report 19–40.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18 (1), 011702.Google Scholar
Jahanbakhshi, R. & Madnia, C. K. 2016 Entrainment in a compressible turbulent shear layer. J. Fluid Mech. 797, 564–603.Google Scholar
Jang, Y. & de Bruyn Kops, S. M. 2007 Pseudo-spectral numerical simulation of miscible fluids with a high density ratio. Comput. Fluids 36 (2), 238–247.Google Scholar
Kaneda, Y. & Ishihara, T. 2006 High-resolution direct numerical simulation of turbulence. J. Turbul. 7, N20.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Knio, O. M. & Ghoniem, A. F. 1992 The three-dimensional structure of periodic vorticity layers under non-symmetric conditions. J. Fluid Mech. 243, 353–392.Google Scholar
Lee, M. J., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561583.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.Google Scholar
Lele, S. K. 1994 Compressibility effects on turbulence. Annu. Rev. Fluid Mech. 26 (1), 211–254.Google Scholar
Mahle, I., Foysi, H., Sarkar, S. & Friedrich, R. 2007 On the turbulence structure in inert and reacting compressible mixing layers. J. Fluid Mech. 593, 171–180.Google Scholar
McMullan, W., Coats, C. & Gao, S. 2011 Analysis of the variable density mixing layer using large eddy simulation. In 41st AIAA Fluid Dynamics Conference and Exhibit, pp. 2011–3424. AIAA.Google Scholar
McMurtry, P. A., Jou, W.-H., Riley, J. & Metcalfe, R. W. 1986 Direct numerical simulations of a reacting mixing layer with chemical heat release. AIAA J. 24 (6), 962–970.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30 (1), 539–578.Google Scholar
Nicoud, F. 2000 Conservative high-order finite-difference schemes for low-Mach number flows. J. Comput. Phys. 158 (1), 71–97.Google Scholar
O’Brien, J., Urzay, J., Ihme, M., Moin, P. & Saghafian, A. 2014 Subgrid-scale backscatter in reacting and inert supersonic hydrogen–air turbulent mixing layers. J. Fluid Mech. 743, 554–584.Google Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.CrossRefGoogle Scholar
Papamoschou, D. & Roshko, A. 1988 The compressible turbulent shear layer: an experimental study. J. Fluid Mech. 197, 453–477.Google Scholar
Peters, N. 2000 Turbulent Combustion. Cambridge University Press.Google Scholar
Pickett, L. M. & Ghandhi, J. B. 2001 Passive scalar measurements in a planar mixing layer by PLIF of acetone. Exp. Fluids 31 (3), 309–318.Google Scholar
Ramshaw, J. D. 2000 Simple model for mixing at accelerated fluid interfaces with shear and compression. Phys. Rev. E 61, 5339–5344.Google Scholar
Reinaud, J., Joly, L. & Chassaing, P. 2000 The baroclinic secondary instability of the two-dimensional shear layer. Phys. Fluids 12 (10), 2489–2505.Google Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6 (2), 903–923.Google Scholar
Sekimoto, A., Dong, S. & Jiménez, J. 2016 Direct numerical simulation of statistically stationary and homogeneous shear turbulence and its relation to other shear flows. Phys. Fluids 28 (3), 035101.Google Scholar
da Silva, C. B. & Pereira, J. C. F 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20 (5), 055101.Google Scholar
Soteriou, M. C. & Ghoniem, A. F. 1995 Effects of the free-stream density ratio on free and forced spatially developing shear layers. Phys. Fluids 7 (8), 2036–2051.Google Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96 (2), 297–324.Google Scholar
Spencer, B. W. & Jones, B. G.1971 Statistical investigation of pressure and velocity fields in the turbulent two-stream mixing layer. AIAA Paper 71-613.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Vreman, A. W., Sandham, N. D. & Luo, K. H. 1996 Compressible mixing layer growth rate and turbulence characteristics. J. Fluid Mech. 320, 235–258.Google Scholar
Wang, P., Fröhlich, J., Michelassi, V. & Rodi, W. 2008 Large-eddy simulation of variable-density turbulent axisymmetric jets. Intl J. Heat Fluid Flow 29 (3), 654–664.Google Scholar
Williams, F. A. 1985 Combustion Theory. Westview Press.Google Scholar
Wyngaard, J. C. 2010 Turbulence in the Atmosphere. Cambridge University Press.Google Scholar