Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T05:10:15.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical study of a turbulent separation bubble with sweep

Published online by Cambridge University Press:  11 October 2019

G. N. Coleman Open the ORCID record for G. N. Coleman [Opens in a new window] ,
C. L. Rumsey  and
P. R. Spalart Open the ORCID record for P. R. Spalart [Opens in a new window]
G. N. Coleman*
Affiliation:
Computational AeroSciences, NASA Langley Research Center, Hampton, VA 23681, USA
C. L. Rumsey
Affiliation:
Computational AeroSciences, NASA Langley Research Center, Hampton, VA 23681, USA
P. R. Spalart
Affiliation:
Boeing Commercial Airplanes, Seattle, WA 98124, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation (DNS) is used to study a separated and rapidly reattached turbulent boundary layer over an idealized 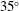$35^{\circ }$ infinite swept wing. The separation and reattachment are induced by a transpiration profile at fixed distance above the layer, with the pressure gradient applied to a well-defined, fully developed, zero-pressure-gradient (ZPG) collateral state. To isolate the influence of the sweep, results are compared with one of our earlier DNS of an unswept flow, with the same chordwise transpiration distribution and appropriate upstream momentum thickness. The independence principle (IP) traditionally proposed for swept wings, which is exact for laminar flows, is found to be close to valid in some regions (bridging the separation/reattachment zone) and to fail in others (in the ZPG layers upstream and downstream of the separation). This is assessed primarily through the skin friction and integral thicknesses. The regions in which the IP is approximately valid correspond to regions of diminished Reynolds-stress divergence, compared to the pressure-gradient magnitude. The mean-velocity profiles exhibit significant skewing as the flow develops, while the velocity magnitude departs only slightly from the ZPG logarithmic profile, even above the separation zone. Implications for Reynolds-averaged turbulence modelling are discussed.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 684 - 706
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van den Berg, B., Elsenaar, A., Lindhout, J. P. F. & Wesseling, P. 1975 Measurements in an incompressible three-dimensional turbulent boundary layer, under infinite swept-wing conditions, and comparison with theory. J. Fluid Mech. 70, 127–148.Google Scholar
Bradshaw, P. 1987 Turbulent secondary flows. Annu. Rev. Fluid Mech. 19, 53–74.Google Scholar
Bradshaw, P. & Pontikos, N. S. 1985 Measurements in the turbulent boundary layer on an ‘infinite’ swept wing. J. Fluid Mech. 159, 105–130.Google Scholar
Coleman, G. N., Ferziger, J. H. & Spalart, P. R.1990 A numerical study of the stratified turbulent Ekman layer. Department of Mechanical Engineering, Stanford University, Thermosciences Div. Rep. TF-48.Google Scholar
Coleman, G. N., Pirozzoli, S., Quadrio, M. & Spalart, P. R. 2017 Direct numerical simulation and theory of a wall-bounded flow with zero skin friction. Flow Turbul. Combust. 99, 553–564.Google Scholar
Coleman, G. N., Rumsey, C. L. & Spalart, P. R. 2018 Numerical study of turbulent separation bubbles with varying pressure gradient and Reynolds number. J. Fluid Mech. 847, 28–70; (referred to herein as CRS18).Google Scholar
Coleman, G. N., Rumsey, C. L. & Spalart, P. R.2019 Numerical study of the the effect of mean three-dimensionality on turbulence in adverse-pressure-gradient boundary layers. NASA TM-2019-220273. Available from NASA Scientific & Technical Information (www.sti.nasa.gov; [email protected]).Google Scholar
Coles, D. E.1962 The turbulent boundary layer in a compressible fluid. Rand Rep. R403-PR, ARC 24473: appendix A: a manual of experimental practice for low-speed flow.Google Scholar
Driver, D. M. & Johnson, J. P.1990 Experimental study of a three-dimensional shear-driven turbulent boundary layer with streamwise adverse pressure gradient. NASA Tech. Mem. 102211.Google Scholar
Eisfeld, B., Rumsey, C. & Togiti, V. 2016 Verification and validation of a second-moment-closure model. AIAA J. 54 (5), 1524–154; Erratum: AIAA J. 54 (9), 2926.Google Scholar
Greenblatt, D., Paschal, K. B., Yao, C.-S., Harris, J., Schaeffler, N. W. & Washburn, A. E. 2006 Experimental investigation of separation control. Part 1. Baseline and steady suction. AIAA J. 44 (12), 2820–2830.Google Scholar
Gruschwitz, E. 1935 Turbulente Reibungsschicten mit Sekundärströmungen. Ing.-Arch 6 (5), 355–365.Google Scholar
Johnston, J. P. 1960 On the three-dimensional turbulent boundary layer generated by secondary flow. Trans. ASME D: J. Basic Engng. 82, 233–248.Google Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in a fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Luchini, P. 2018 Structure and interpolation of the turbulent velocity profile in parallel flow. Eur. J. Mech. (B/Fluids) 71, 15–34.Google Scholar
McLean, D. J. 2013 Understanding Aerodynamics – Arguing from the Real Physics, p. 550. Wiley.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578.Google Scholar
Prandtl, L. 1945 Über Reibungsschichten bei dreidimensionalen Strömungen. Betz-Festschrift 134–141.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Schubauer, G. B. & Tchen, C. M. 1959 Turbulent flow: general treatment of incompressible mean flow along walls. In Turbulent Flows and Heat Transfer (ed. Lin, C. C.), section B: chap. 4, p. 549. Princeton University Press.Google Scholar
Slotnick, J., Khodadoust, A., Alanso, J., Darmofal, D., Gropp, W., Lurie, E. & Mavriplis, D.2014 CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences NASA CR 2014-218178. Available from NASA Technical Reports Server (https://ntrs.nasa.gov).Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to R 𝜃 = 1410. J. Fluid Mech. 187, 61–98.Google Scholar
Spalart, P. R. & Allmaras, S. R. 1994 A one-equation turbulence model for aerodynamic flows. Rech. Aerosp. 1, 5–21.Google Scholar
Spalart, P. R. & Coleman, G. N. 1997 Numerical study of a separation bubble with heat transfer. Eur. J. Mech. (B/Fluids) 16, 169–189; (referred to herein as SC97).Google Scholar
Spalart, P. R., Coleman, G. N. & Johnstone, R. 2009 Retraction: ‘Direct numerical simulation of the Ekman layer: a step in Reynolds number, and cautious support for a log law with a shifted origin’. Phys. Fluids 21, 109901.Google Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral solvers for the Navier–Stokes equations with two periodic and one infinite direction. J. Comput. Phys. 96, 297–324.Google Scholar
Spalart, P. R. & Watmuff, J. H. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 249, 337–371.Google Scholar
Stratford, B. S. 1959 The prediction of separation of the turbulent boundary layer. J. Fluid Mech. 5, 1–16.Google Scholar
White, F. M. 1991 Viscous Fluid Flow, p. 614. McGraw-Hill.Google Scholar
Wu, W., Meneveau, C. & Mittal, R. 2019 Dynamics of natural and perturbed turbulent separation bubbles. In Eleventh International Symposium on Turbulence and Shear Flow Phenomena (TSFP11), Southampton, UK, 30 July–2 August, 2019.Google Scholar
Wygnanski, I., Tewes, P. & Tauber, L. 2014 Applying the boundary-layer independence principle to turbulent flows. J. Aircraft. 51 (1), 175–182.Google Scholar