Published online by Cambridge University Press: 04 September 2019
The linear instability of a vortex ring with swirl with Gaussian distributions of azimuthal vorticity and velocity in its core is studied by direct numerical simulation. The numerical study is carried out in two steps: first, an axisymmetric simulation of the Navier–Stokes equations is performed to obtain the quasi-steady state that forms a base flow; then, the equations are linearized around this base flow and integrated for a sufficiently long time to obtain the characteristics of the most unstable mode. It is shown that the vortex rings are subjected to curvature instability as predicted analytically by Blanco-Rodríguez & Le Dizès (J. Fluid Mech., vol. 814, 2017, pp. 397–415). Both the structure and the growth rate of the unstable modes obtained numerically are in good agreement with the analytical results. However, a small overestimation (e.g. 22 % for a curvature instability mode) by the theory of the numerical growth rate is found for some instability modes. This is most likely due to evaluation of the critical layer damping which is performed for the waves on axisymmetric line vortices in the analysis. The actual position of the critical layer is affected by deformation of the core due to the curvature effect; as a result, the damping rate changes since it is sensitive to the position of the critical layer. Competition between the curvature and elliptic instabilities is also investigated. Without swirl, only the elliptic instability is observed in agreement with previous numerical and experimental results. In the presence of swirl, sharp bands of both curvature and elliptic instabilities are obtained for 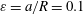 $\unicode[STIX]{x1D700}=a/R=0.1$, where
$\unicode[STIX]{x1D700}=a/R=0.1$, where  $a$ is the vortex core radius and
$a$ is the vortex core radius and 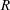 $R$ the ring radius, while the elliptic instability dominates for
$R$ the ring radius, while the elliptic instability dominates for 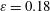 $\unicode[STIX]{x1D700}=0.18$. New types of instability mode are also obtained: a special curvature mode composed of three waves is observed and spiral modes that do not seem to be related to any wave resonance. The curvature instability is also confirmed by direct numerical simulation of the full Navier–Stokes equations. Weakly nonlinear saturation and subsequent decay of the curvature instability are also observed.
$\unicode[STIX]{x1D700}=0.18$. New types of instability mode are also obtained: a special curvature mode composed of three waves is observed and spiral modes that do not seem to be related to any wave resonance. The curvature instability is also confirmed by direct numerical simulation of the full Navier–Stokes equations. Weakly nonlinear saturation and subsequent decay of the curvature instability are also observed.