Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T14:35:47.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of turbulent supersonic axisymmetric wakes

Published online by Cambridge University Press:  07 June 2012

Richard D. Sandberg
Richard D. Sandberg*
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Numerical experiments are conducted of turbulent supersonic axisymmetric wakes at Mach number 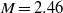and Reynolds number, based on free-stream velocity and base diameter, 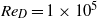. Direct numerical simulations (DNS) are used to study the effect of approach flow conditions, and of specific azimuthal modes, on the near-wake behaviour. To that end, DNS are performed with laminar and turbulent approach boundary layers, and additional turbulent approach flow DNS with reduced circumferential size are conducted to deliberately eliminate certain azimuthal/helical modes. DNS with turbulent approach flow show an increased turning angle and increased growth of the separating shear layer, leading to a shorter recirculation region, a stronger recompression shock system, and ultimately good agreement with experimental data at considerably higher Reynolds number. A similar wake structure is found for laminar and turbulent inflow conditions, giving further evidence of the wake structure being a consequence of the global near-wake instabilities and not a result of upstream conditions. Stability analyses of two-dimensional basic states are carried out by computing the temporal pulse response using forced Navier–Stokes simulations to investigate which azimuthal modes are dominant for fully turbulent wakes and how the stability behaviour is influenced by the choice of basic state. Using the time- and azimuthally averaged data from three-dimensional DNS with turbulent inflow as basic state, an absolute instability of the axisymmetric mode was found and helical modes 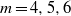were found to be linearly most unstable, in contrast to results obtained earlier using an axisymmetric flow solution as the basic state. The addition of a turbulence viscosity in the forced DNS retains most of the stability characteristics but reduces the wavenumber of the linearly most-amplified modes.

JFM classification

Instability: Absolute/convective instability Turbulent Flows: Turbulent transition Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 702 , 10 July 2012 , pp. 488 - 520
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alfredsson, P., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the outer peak. Phys. Fluids 23, 041702.CrossRefGoogle Scholar
2. Barnhardt, M. & Candler, G. 2006 Detached eddy simulation of hypersonic base flows during atmospheric entry. AIAA Paper 2006-3575.Google Scholar
3. Bogey, C., de Cacqueray, N. & Bailly, C. 2009 A shock-capturing methodology based on adaptative spatial filtering for high-order non-linear computations. J. Comput. Phys. 228 (5), 1447–1465.Google Scholar
4. Bourdon, C. J. & Dutton, J. C. 1998 Planar visualizations of large-scale turbulent structures in axisymmetric supersonic separated flows. Phys. Fluids 11, 201–213.Google Scholar
5. Bourdon, C. J. & Dutton, J. C. 2001 Effects of boattailing on the turbulence structure of a compressible base flow. J. Spacecr. Rockets 38 (4), 534–541.CrossRefGoogle Scholar
6. Bowman, W. C. & Clayden, W. A. 1968 Boat-tailed afterbodies at with gas ejection. AIAA J. 2, 2029.Google Scholar
7. Coleman, G., Kim, J. & Moser, R. 1995 A numerical study of turbulent supersonic isothermal-wall channel flow. J. Fluid Mech. 305, 159–183.Google Scholar
8. Cortwright, E. M. & Schroeder, A. H. 1951 Preliminary investigation of effectiveness of base bleed in reducing drag of blunt-base bodies in supersonic stream. NACA Rep. RM E51 A26. National Advisory Committee for Aeronautics.Google Scholar
9. Deck, S. & Thorigny, P. 2007 Unsteadiness of an axisymmetric separating-reattaching flow: numerical investigation. Phys. Fluids 19, 065103.CrossRefGoogle Scholar
10. Demetriades, A. 1968 Turbulence front structure of an axisymmetric compressible wake. J. Fluid Mech. 34, 465–480.CrossRefGoogle Scholar
11. Demetriades, A. 1976 Turbulence correlations in a compressible wake. J. Fluid Mech. 74, 251–267.CrossRefGoogle Scholar
12. Forsythe, J. R., Hoffmann, K. A. & Squires, K. D. 2002 Detached-eddy simulation with compressibility corrections applied to a supersonic axisymmetric base flow. AIAA Paper2002-0586.Google Scholar
13. Fureby, C. 1999 Large eddy simulation of supersonic baseflow. AIAA Paper 99-0426.Google Scholar
14. Herrin, J. L. & Dutton, J. C. 1989 Supersonic base flow experiments in the near wake of a cylindrical afterbody. J. Fluid Mech. 199, 55–88.Google Scholar
15. Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
16. Jones, L. E., Sandberg, R. & Sandham, N. 2010 Stability and receptivity characteristics of a laminar separation bubble on an aerofoil. J. Fluid Mech. 648, 257–296.Google Scholar
17. Kawai, S. & Fujii, K. 2005 Computational study of supersonic base flow using hybrid turbulence methodology. AIAA J. 43 (6), 1265–1275.CrossRefGoogle Scholar
18. Kennedy, C., Carpenter, M. & Lewis, R. 2000 Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations. Appl. Numer. Maths 35, 177–219.Google Scholar
19. Kennedy, C. & Gruber, A. 2008 Reduced aliasing formulations of the convective terms within the Navier–Stokes equations for a compressible fluid. J. Comput. Phys. 227, 1676–1700.CrossRefGoogle Scholar
20. Klein, M., Sadiki, A. & Janicka, J. 2003 A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 186 (2), 652–665.CrossRefGoogle Scholar
21. Lund, T., Wu, X. & Squires, K. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140 (2), 233–258.Google Scholar
22. Mack, L. 1975 Linear stability theory and the problem of supersonic boundary-layer transition. AIAA J. 13, 278–289.Google Scholar
23. Mathur, T. & Dutton, C. 1996 Velocity and turbulence measurements in a supersonic base flow with mass bleed. AIAA J. 34, 1153.Google Scholar
24. Meliga, P., Sipp, D. & Chomaz, J. 2008 Absolute instability in axisymmetric wakes: compressible and density variation effects. J. Fluid Mech. 600, 373–401.CrossRefGoogle Scholar
25. Meliga, P., Sipp, D. & Chomaz, J. 2010 Effect of compressibility on the global stability of axisymmetric wake flows. J. Fluid Mech. 660, 499–526.Google Scholar
26. Pamiès, M., Weiss, P., Garnier, E., Deck, S. & Sagaut, P. 2009 Generation of synthetic turbulent inflow data for large eddy simulation of spatially evolving wall-bounded flows. Phys. Fluids 21, 045103.CrossRefGoogle Scholar
27. Rollstin, L. 1990 Measurement of inflight base-pressure on an artillery-fired projectile. J. Spacecr. Rockets 27 (1), 5–6.Google Scholar
28. Sahu, J. & Heavey, K. R. 1995 Numerical investigation of supersonic base flow with base bleed. J. Spacer. Rockets 34 (1), 61–69.Google Scholar
29. Sahu, J., Nietubicz, C. & Steger, J. 1985 Navier–Stokes computations of projectile base flow with and without mass injection. AIAA J. 23 (9), 1348–1355.CrossRefGoogle Scholar
30. Sandberg, R. D. 2011 An axis treatment for flow equations in cylindrical coordinates based on parity conditions. Comput. Fluids 49, 166–172.CrossRefGoogle Scholar
31. Sandberg, R. D. & Fasel, H. F. 2006a Direct numerical simulations of transitional supersonic base flows. AIAA J. 44 (4), 848–858.CrossRefGoogle Scholar
32. Sandberg, R. D. & Fasel, H. F. 2006b Investigation of supersonic wakes using conventional and hybrid turbulence models. AIAA J. 44 (9), 2071–2083.Google Scholar
33. Sandberg, R. D. & Fasel, H. F. 2006c Numerical investigation of transitional supersonic axisymmetric wakes. J. Fluid Mech. 563, 1–41.CrossRefGoogle Scholar
34. Sandberg, R. D. & Sandham, N. D. 2008 Direct numerical simulation of turbulent flow past a trailing edge and the associated noise generation. J. Fluid Mech. 596, 353–385.CrossRefGoogle Scholar
35. Sandberg, R., Suponitsky, V. & Sandham, N. 2012 DNS of compressible pipe flow exiting into a coflow. Intl J. Heat Fluid Flow doi:10.1016/j.ijheatfluidflow.2012.01.006.CrossRefGoogle Scholar
36. Sandham, N., Li, Q. & Yee, H. 2002 Entropy splitting for high-order numerical simulation of compressible turbulence. J. Comput. Phys. 178, 307–322.CrossRefGoogle Scholar
37. Sandham, N., Yao, Y. & Lawal, A. 2003 Large-eddy simulation of transonic flow over a bump. Intl J. Heat Transfer Fluid Flow 24, 584–595.CrossRefGoogle Scholar
38. Schlichting, H. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
39. Simon, F., Deck, S., Guillen, P., Sagaut, P. & Merlen, A. 2007 Numerical simulation of the compressible mixing layer past an axisymmetric trailing edge. J. Fluid Mech. 591, 215–254.Google Scholar
40. Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to . J. Fluid Mech. 187, 61–98.Google Scholar
41. Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 39, 249–315.CrossRefGoogle Scholar
42. Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.Google Scholar
43. Touber, E. & Sandham, N. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.CrossRefGoogle Scholar
44. Walpot, L., Wright, M., Noeding, P. & Schrijer, F. 2012 Base flow investigation of the Apollo AS-202 command module. Prog. Aeronaut. Sci 48–49, 57–74.Google Scholar
45. White, F. M. 1991 Viscous Fluid Flow. McGraw Hill.Google Scholar
46. Wu, X. & Moin, P. 2008 A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 608, 81–112.Google Scholar
47. Xie, Z. & Castro, I. 2008 Efficient generation of inflow conditions for large-eddy simulation of street-scale flows. Flow Turbul. Combust. 81 (3), 449–470.Google Scholar