Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T02:41:54.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of the flow dynamics past a three-element aerofoil

Published online by Cambridge University Press:  06 September 2013

Sébastien Deck  and
Romain Laraufie
Sébastien Deck*
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
Romain Laraufie
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A numerical investigation of the flow dynamics around a two-dimensional high-lift configuration was carried out by means of a zonal detached eddy simulation (ZDES) technique for flow conditions corresponding to aircraft approach. Both slat and flap regions have been scrutinized and compared with experimental data available in the literature. It is shown that slat and flap coves behave like shallow cavities. The distance between the upstream cusp and the downstream edge is the relevant length scale for each cove taken separately. 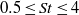Consistently with previous findings, this study indicates that the maximum of the broadband spectrum of slat (respectively flap) pressure fluctuations occurs for Strouhal numbers $0. 5\leq \mathit{St}\leq 4$ when based on slat chord (respectively on flap chord) and free-stream velocity. It is shown that mode 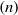$(n)$ of the slat cove and mode 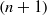$(n+ 1)$ of the flap cove are very close making a coherent phase relationship possible. A large-scale coupled self-sustained oscillations mechanism between slat and flap cavities, evidenced by spectral analysis, occurs at a Strouhal number 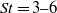$\mathit{St}= 3{\unicode{x2013}} 6$ based on the main wing chord and free-stream velocity. This yields to an acoustic feedback mechanism characterized by a normalized frequency depending on the free stream Mach number like 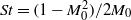$\mathit{St}= (1- { M}_{0}^{2} )/ 2{M}_{0} $. The present result appears to line up with the findings by Hein et al. (J. Fluid Mech., vol. 582, 2007, pp. 179–202) who showed that two types of resonance could exist: surface waves ones, scaling with the total aerofoil length and longitudinal cavity-type resonances, scaling with the slat cove length.

JFM classification

Acoustics: Aeroacoustics Aerodynamics: Aerodynamics Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 732 , 10 October 2013 , pp. 401 - 444
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agarwal, A. & Morris, P. J. 2002 Investigation of the physical mechanisms of tonal sound generation by slats. AIAA Paper 2002-2575.Google Scholar
Arnott, K., Neitzke, K. P., Agocs, J., Sammer, G., Schneider, G. & Schroeder, A. 2003 Detailed characterisation using PIV of the flow around an aerofoil in high lift configuration. In EUROPIV2 Workshop on Particle Image Velocimetry. Springer.Google Scholar
Block, P. J. W. 1976 Noise response of cavities of varying dimensions at subsonic speeds. NASA Tech. Note D-8351.Google Scholar
Brooks, T. F. & Humphreys, W. M. 2003 Flap-edge aeroacoustic measurements and predictions. J. Sound Vib. 261, 31–74.Google Scholar
Burt, M. 1994 A selection of experimental test cases of CFD codes: chapter 5 - summaries of test cases. AGARD Rep. AR-303, vol. 1, pp. 55–133.Google Scholar
Capon, J. 1978 High-resolution frequency–wavenumber spectrum analysis. In Modern Spectrum Analysis (ed. Childers, D. G.). pp. 119–129. IEEE.Google Scholar
Chen, L. W., Wang, G. L. & Lu, X. Y. 2011 Numerical investigation of a jet from a blunt body opposing a supersonic flow. J. Fluid Mech. 684, 85–110.CrossRefGoogle Scholar
Chen, L. W., Xu, C. Y. & Lu, X. Y. 2010 Numerical investigation of the compressible flow past an aerofoil. J. Fluid Mech. 643, 97–216.Google Scholar
Choi, H. & Moin, P. 1994 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 113 (1), 227–234.Google Scholar
Choi, H. & Moin, P. 2012 Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 24, 011702.Google Scholar
Choudhari, M. & Khorrami, M. R. 2007 Effect of three-dimensional shear-layer structures on slat cove unsteadiness. AIAA J. 45 (9), 2174–2186.CrossRefGoogle Scholar
Chow, L., Mau, K. & Remy, H. 2002 Landing gears and high lift devices airframe noise research. AIAA Paper 2002-2408.Google Scholar
Dandois, J., Garnier, E. & Sagaut, P. 2007 Numerical simulation of active separation control by a synthetic jet. J. Fluid Mech. 574, 25–58.Google Scholar
Dargel, G. & Schnieder, H. 1989 Garteur high-lift action group (ag08). GARTEUR AD (AG08) Final Report.Google Scholar
Deck, S. 2005a Numerical simulation of transonic buffet over a supercritical aerofoil. AIAA J. 43 (7), 1556–1566.Google Scholar
Deck, S. 2005b Zonal-detached eddy simulation of the flow around a high-lift configuration. AIAA J. 43 (11), 2372–2384.Google Scholar
Deck, S. 2012a Advanced turbulence modelling for aeroacoustics sources calculations. Application of zonal detached eddy simulation (ZDES). In Airframe Noise (ed. Denos, R., Lecomte, E., Kors, E. & Schram, C.). Von Kármán Institute Lecture Series LS 2012-02.Google Scholar
Deck, S. 2012b Recent improvements of the zonal detached eddy simulation (ZDES) formulation. Theor. Comput. Fluid Dyn. 26 (6), 523–550.Google Scholar
Deck, S., Duveau, Ph., d’Espiney, P. & Guillen, Ph. 2002 Development and application of Spalart Allmaras one equation turbulence model to three-dimensional supersonic complex configurations. Aerosp. Sci. Technol. 6 (3), 171–183.Google Scholar
Deck, S. & Thorigny, P. 2007 Unsteadiness of an axisymmetric separating-reattaching flow: numerical investigation. Phys. Fluids 19, 065103.Google Scholar
Deck, S., Weiss, P. E., Pamiès, M. & Garnier, E. 2011 Zonal detached eddy simulation of a spatially developing flat plate turbulent boundary layer. Comput. Fluids 48, 1–15.Google Scholar
Delfs, J. 2012 Airframe noise. In Airframe’ Noise (ed. Denos, R., Lecomte, E., Kors, E. & Schram, C.). Von Kármán Institute Lecture Series LS 2012-02.Google Scholar
Dillner, B. 1984 Aerodynamics issues in the design of highlift systems for transport aircraft. CP365, AGARD, Paper 9.Google Scholar
Dobrzynski, W. 2010 Almost 40 years of airframe noise research: What did we achieve? J. Aircraft 47 (2), 353–367.CrossRefGoogle Scholar
Dobrzynski, W. & Pott-Polenske, M. 2001 Slat noise source studies for farfield prediction. AIAA Paper 2001-2158.Google Scholar
Fink, M. R. 1977 Airframe noise prediction method. FAA-RD-77-29.Google Scholar
Fink, M. R. 1979 Noise component method for airframe noise. J. Aircraft 16 (10), 659–665.Google Scholar
Gand, F., Deck, S., Brunet, V. & Sagaut, P. 2010 Dynamics over a simplified junction flow. Phys. Fluids 22, 115111.CrossRefGoogle Scholar
Glatzer, C., Meiß, J.-H., Meike, M. & Schröder, W. 2011 Numerical investigation of the nearwake of generic space launcher systems at transonic and supersonic flows. In 4th European Conference For Aerospace Science, Saint Petersburg, Russia.Google Scholar
Guo, Y. 2001 A discrete vortex model for slat noise prediction. AIAA Paper 2001-2157.Google Scholar
Guo, Y. 2010 Aircraft slat noise modelling and prediction. AIAA Paper 2010-3837.Google Scholar
Guo, Y. 2011 Aircraft flap side edge noise modelling and prediction. AIAA Paper 2011-574.CrossRefGoogle Scholar
Guo, Y. P., Joshi, M. C., Bent, P. H. & Yamamoto, K. J. 2000 Surface pressure fluctuations on aircraft flaps and their correlation with farfield noise. J. Fluid Mech. 415, 175–202.CrossRefGoogle Scholar
Hein, S., Hohage, T., Koch, W. & Schoberl, J. 2007 Acoustic resonances in high-lift configuration. J. Fluid Mech. 582, 179–202.Google Scholar
Heller, H. H. & Bliss, D. B. 1975 The physical mechanism of flow-induced pressure fluctuations in cavities and concepts for their suppressions. AIAA Paper 75-491, 2nd AIAA Aero-Acoustics Conference, Hampton, Virginia, March.Google Scholar
Henning, A., Kaepernick, K., Ehrenfried, K., Koop, L. & Dillmann, A. 2008 Investigation of aeroacoustic noise generation by simultaneous particle image velocimetry and microphone measurements. Exp. Fluids 45, 1073–1085.Google Scholar
Henning, A., Wrede, B. & Geisler, R. H. 2012 Aeroacoustic investigation of a high-lift device by means of synchronized PIV and microphone measurements. In 16th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, 9–12 July.Google Scholar
Ho, C. M. & Nosseir, N. S. 1981 Dynamics of an impinging jet. Part 1. The feedback phenomenon. J. Fluid Mech. 105, 119–142.CrossRefGoogle Scholar
Huang, L. S. & Ho, C. M. 1982 Small scale transition in a plane mixing layer. J. Fluid Mech. 200, 475–500.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Imamura, T., Enomoto, S., Yokokawa, Y. & Tamamoto, K. 2008 Three-dimensional unsteady flow computations around a conventional slat of high-lift devices. AIAA J. 46 (5), 1045–1053.CrossRefGoogle Scholar
Jenkins, L. N., Khorrami, M. R., Choudhari, & M, 2004 Characterization of unsteady flow structures near leading-edge slat: part I. PIV measurements. AIAA Paper 2004-2802, 10th AIAA/CEAS Aeroacoustics Conference.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Kaepernick, K., Koop, L. & Ehrenfried, K. 2007 Investigation of the unsteady flow field inside a leading edge slat cove. AIAA Paper 2005-2813.CrossRefGoogle Scholar
Keating, A., De Prisco, G. & Piomelli, U. 2006 Interface conditions for hybrid RANS/LES calculations. Intl J. Heat Fluid Flow 27, 777–788.Google Scholar
Keating, A. & Piomelli, U. 2006 A dynamic stochastic forcing method as a wall-layer model for large-eddy simulation. J. Turbul. 7 (12), 1–24.CrossRefGoogle Scholar
Keating, A., Piomelli, U., Balaras, E. & Kaltenbach, H. J. 2004 A priori and a posteriori tests of inflow conditions for large-eddy simulation. Phys. Fluids 16 (12), 4696–4712.Google Scholar
Knacke, T. & Thiele, F. 2010 Time resolved 3D simulation of an aircraft wing with deployed high-lift system. In Turbulence & Interaction, Notes on Numerical Fluid Mechanics and Multidisciplinary Design, Vol. 110. pp. 223–230. Springer.Google Scholar
Kok, J. C. & Van der Ven, H. 2012 Capturing shear layers in hybrid RANS-LES simulations of separated flows. In Second symposium of Wing and Nacelle Stall, Braunschweig (Germany), 20–21 June.Google Scholar
Kolb, A., Faulhaber, P., Drobietz, R. & Grunwald, M. 2007 Aeroacoustic wind tunnel measurements on a 2D high-lift configuration. AIAA Paper 2007-3447.CrossRefGoogle Scholar
Konig, D., Koh, S. R., Meinke, M. & Schroder, W. 2010 Two-step simulation of slat noise. Comput. Fluids 39, 512–524.Google Scholar
Laraufie, R. & Deck, S. 2013 Assessment of Reynolds stresses tensor reconstruction methods for synthetic inflow conditions. application to hybrid RANS/LES methods. Intl J. Heat Fluid Flow 42, 68–78.Google Scholar
Laraufie, R., Deck, S. & Sagaut, P. 2011 A dynamic forcing method for unsteady turbulent inflow conditions. J. Comput. Phys. 230 (23), 8647–8663.Google Scholar
Laraufie, R., Deck, S. & Sagaut, P. 2012 A rapid switch from RANS to WMLES for spatially developing boundary layers. In Progress in Hybrid RANS-LES Modelling (ed. Fu, S., Haase, W., Peng, S.-H. & Schwamborn, D.). Notes on Numerical Fluid Mechanics and Multidisciplinary Design, Vol. 117. pp. 147–156. Springer.Google Scholar
Larchevêque, L., Sagaut, P., Le, T. H. & Comte, P. 2004 Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number. J. Fluid Mech. 516, 265–301.Google Scholar
Lee, S. H., Kim, J. R., Ba, Y., Jo, Y. W. & Moon, Y. J. 2010 Computation of slat noise by a LES/LPCE hybrid method with Brinkman penalization. AIAA Paper 2010-3829.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Lockard, D. P. & Choudhari, M. 2009 Noise radiation from a leading-edge slat. AIAA Paper 09-3101, 15th AIAA/CEAS Aeroacoustics Conference, Miami, Florida.Google Scholar
Ma, Z. & Zhang, X. 2009 Numerical investigation of broadband slat noise attenuation with acoustic liner treatment. AIAA J. 47 (12), 2812–2820.Google Scholar
Mabey, D. G. 1972 Analysis and correlation of data on pressure fluctuations in separated flow. J. Aircraft 9 (9), 642–645.Google Scholar
Mary, I. & Sagaut, P. 2002 Large eddy simulation of flow around an aerofoil near stall. AIAA J. 40 (6), 1139–1145.CrossRefGoogle Scholar
Mendoza, J. M. & Brooks, T. F. 2002 Aeroacoustic measurement of a wing/slat model. AIAA Paper 2002-2604.CrossRefGoogle Scholar
Monkewitz, P. A. & Huerre, P. 1982 Influence of the velocity ratio on the instability of mixing layers. Phys. Fluids 25 (7), 1137–1143.Google Scholar
Nebenfuhr, B., Peng, S.-H. & Davidson, L. 2012 Hybrid RANS-LES simulation of turbulent high-lift flow in relation to noise generation. In Progress in Hybrid RANS-LES Modelling (ed. Fu, S., Haase, W., Peng, S.-H. & Schwamborn, D.). Notes on Numerical Fluid Mechanics and Multidisciplinary Design, Vol. 117. pp. 303–314. Springer.Google Scholar
Pamiès, M., Garnier, E., Merlen, A. & Sagaut, P. 2007 Response of a spatially developping turbulent boundary layer to active control strategies in the framework of opposition control. Phys. Fluids 19, 108102.Google Scholar
Pamiès, M., Weiss, P. E., Garnier, E., Deck, S. & Sagaut, P. 2009 Generation of synthetic turbulent inflow data for large eddy simulation of spatially evolving wall-bounded flows. Phys. Fluids 21, 045103.Google Scholar
Paschal, K., Jenkins, L. & Yao, C. 2000 Unsteady slat-wake characteristics of a high-lift configuration. AIAA Paper 00-0139, 38th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada.Google Scholar
Péchier, M., Guillen, Ph. & Caysac, R. 2001 Magnus effect over finned projectiles. AIAA J. Spacecr. Rockets 38 (4), 542–549.Google Scholar
Perennes, S. & Roger, M. 1998 Aerodynamic noise of a two-dimensional wing with high-lift devices. AIAA Paper 98-2338.Google Scholar
Piet, J. F., Michel, U. & Bohning, P. 2002 Localization of the acoustic sources of the a340 with a large phased microphone array during flight tests. AIAA Paper 2002-2506.Google Scholar
Poletto, R., Revell, A., Craft, T. & Jarrin, N. 2011 Divergence free synthetic eddy method for embedded LES inflow conditions. In 7th International Symposium on Turbulence and Shear Flow Phenomena, Ottawa.Google Scholar
Reuß, S., Knopp, T. & Schwamborn, D. 2012 Hybrid RANS/LES simulations of a three-element aerofoil. In Progress in Hybrid RANS-LES Modelling (ed. Fu, S., Haase, W., Peng, S.-H. & Schwamborn, D.). Notes on Numerical Fluid Mechanics and Multidisciplinary Design, Vol. 117. pp. 357–367. Springer.CrossRefGoogle Scholar
Rockwell, D. 1983 Oscillations of impinging shear layers. AIAA J. 21 (5), 645–664.Google Scholar
Rockwell, D. & Naudasher, E. 1979 Self-sustained oscillations of impinging free shear layers. Annu. Rev. Fluid Mech. 11, 67–94.Google Scholar
Roger, M. & Perennes, S. 2000 Low-frequency noise sources in two-dimensional high-lift devices. AIAA Paper 2000-1972.Google Scholar
Roidl, B., Meinke, M. & Schröder, W. 2011 Numerical investigation of shock wave boundary-layer interaction using a zonal RANS-LES ansatz. In High Performance Computing in Science and Engineering’10 (ed. Nagel, W. E., Kröner, D. B. & Resch, M. M.). pp. 369–383. Springer.Google Scholar
Rossiter, J. 1964 Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Aeronautical Research Council, Tech. Rep. RM 3438.Google Scholar
Rumsey, C. L. & Ying, S. X. 2002 Prediction of high lift: review of present CFD capability. Prog. Aerosp. Sci. 38, 145–180.CrossRefGoogle Scholar
Sagaut, P. & Deck, S. 2009 Large eddy simulation for aerodynamics: status and perpectives. Phil. Trans. R. A 367, 2849–2860.Google Scholar
Sagaut, P., Deck, S. & Terracol, M. 2006 Multiscale and Multiresolution Approaches in Turbulence. Imperial College Press.Google Scholar
Satti, R., Li, Y., Shock, R. & Noelting, S. 2012 Unsteady flow analysis of a multi-element aerofoil using lattice Boltzmann method. AIAA J. 50 (9), 1805–1816.Google Scholar
Shur, M. L., Spalart, P. R. & Strelets, M. 2005 Noise prediction for increasingly complex jets. Part I: Methods and tests. Intl J. Aeroacoust. 4, 247–256.Google Scholar
Simon, F., Deck, S., Guillen, Ph., Sagaut, P. & Merlen, A. 2007 Numerical simulation of the compressible mixing layer past an axisymmetric trailing edge. J. Fluid Mech. 591, 215–253.Google Scholar
Smith, A. M. O. 1975 High-lift aerodynamics. J. Aircraft 12 (6), 501–530.Google Scholar
Spaid, F. W. 2000 High Reynolds number multielement aerofoil flow field measurements. J. Aircraft 37 (3), 499–507.Google Scholar
Spalart, P. R. 2000 Strategies for turbulence modelling and simulations. Intl J. Heat Fluid Flow 21 (3), 252–263.Google Scholar
Spalart, P. R. 2009 Detached eddy simulation. Annu. Rev. Fluid Mech. 41, 181–202.Google Scholar
Spalart, P. R. & Allmaras, S. R. 1994 A one equation turbulence model for aerodynamic flows. La Rech. Aérospatiale 1, 5–21.Google Scholar
Spalart, P. R., Deck, S., Shur, M. L., Squires, K. D., Strelets, M. & Travin, A. 2006 A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 20, 181–195.Google Scholar
Spalart, P., Jou, W. H., Strelets, M. & Allmaras, S. R. 1998 Comments on the feasibility of LES for wings and on a hybrid RANS/LES approach. In Proceedings 1st AFSOR International Conference on DNS/LES, Ruston, pp. 137–147.Google Scholar
Spazzini, P. G., Iuso, G., Onorato, M., Zurlo, N. & Di Cicca, G. M. 2001 Unsteady behaviour of back-facing flow. Exp. Fluids 30, 551–561.Google Scholar
Spille-Kohoff, A. & Kaltenbach, H. J. 2001 Generation of turbulent inflow data with a described shear-stress profile. In Proceedings of the Third AFOSR International Conference on DNS/LES, Arlington, 5–9 August (ed. Liu, C., Sakell, L. & Beutner, T.). pp. 137–147. Greyden.Google Scholar
Stoker, R. W., Guo, Y., Streett, C. & Burnside, N. 2003 Airframe noise source locations of a 777 aircraft in flight and comparisons with past model scale tests. AIAA Paper 2003-3232.Google Scholar
Tabor, G. R. & Baba-Ahmadi, M. H. 2010 Inlet conditions for large eddy simulation: a review. Comput. Fluids 39 (4), 553–567.Google Scholar
Takeda, K., Ashcrott, G. B., Zhang, X. & Nelson, P. A. 2001a Unsteady aerodynamics of flap cove flow in a high-lift device configuration. AIAA Paper 2001-0707, 39th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, January.Google Scholar
Takeda, K., Ashcrott, G. B., Zhang, X. & Nelson, P. A. 2001b Unsteady aerodynamics of slat cove flow in a high-lift device configuration. AIAA Paper 2001-0706, 39th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, January.Google Scholar
Takeda, K., Zhang, X. & Nelson, P. A. 2002 Unsteady aerodynamics and aeroacoustics of a high-lift configuration. AIAA Paper 2002-0570, 40th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, January.Google Scholar
Takeda, K., Zhang, X. & Nelson, P. 2011 Computational aeroacoustic simulations of leading edge slat flows. J. Sound Vib. 270, 559–572.Google Scholar
Tam, C. K. W. 1974 Discrete tones of isolated aerofoils. J. Acoust. Soc. Am. 55 (6), 1173–1177.Google Scholar
Tam, C. K. W. & Pastouchenko, N. 2000 Gap tones: a component of airframe noise. AIAA Paper 2000-606.CrossRefGoogle Scholar
Terracol, M. 2006 A zonal RANS/LES approach for noise sources prediction. Flow Turbul. Combust. 77, 161–184.Google Scholar
Terracol, M. & Deck, S. 2012 Numerical investigation of the flow around a three-element high-lift aerofoil using two zonal hybrid RANS/LES methods: ZDES and NLDE. In Progress in Hybrid RANS-LES Modelling (ed. Fu, S., Haase, W., Peng, S.-H. & Schwamborn, D.). Notes on Numerical Fluid Mechanics and Multidisciplinary Design, Vol. 117. pp. 345–355. Springer.Google Scholar
Terracol, M., Manoha, E., Herrero, E., Labourasse, E., Redonnet, S. & Sagaut, P. 2005 Hybrid methods for airframe noise numerical prediction. Theor. Comput. Fluid Dyn. 19 (3), 197–227.Google Scholar
Terracol, M., Manoha, E. & Lemoine, B. 2011 Investigation of the unsteady flow and noise sources generation in a slat cove: hybrid zonal RANS/LES simulation and dedicated experiment. AIAA Paper 2011-3203.Google Scholar
Thompson, B. E. & Whitelaw, J. H. 1985 Characteristics of a trailing-edge flow with turbulent boundary-layer separation. J. Fluid Mech. 157, 305–326.Google Scholar
Uzun, A. & Hussaini, M. Y. 2012 An application of delayed detached eddy simulation to tandem cylinder flow field prediction. Comput. Fluids 60, 71–85.CrossRefGoogle Scholar
van Dam, C. P. 2002 The aerodynamic design of multi-element systems for transport airplanes. Prog. Aerosp. Sci. 38, 101–144.Google Scholar
Wang, M., Lele, S. K. & Moin, P. 1996 Computation of quadrupole noise using acoustic analogy. AIAA J. 34 (11), 2247–2254.Google Scholar
Weiss, P. E. & Deck, S. 2011 Control of the antisymmetric mode $(m= 1)$ for high Reynolds axisymmetric separating/reattaching flows. Phys. Fluids 23, 095102.Google Scholar
Weiss, P. E., Deck, S., Sagaut, P. & Robinet, J. C. 2009 On the dynamics of axisymmetric turbulent separating/reattaching flow. Phys. Fluids 21, 075103.Google Scholar
Wild, J. 2012 Experimental investigation of Mach and Reynolds number dependencies of the stall of 2-element and 3-element high-lift wing sections. AIAA Paper 2012-0108.Google Scholar
Wild, J., Pott-Pollenske, M. & Nagel, B. 2006 An integrated design approach for low noise exposing high-lift devices. AIAA Paper 2006-2843.Google Scholar
Zhang, Q., Schröder, W. & Meinke, M. 2010 A zonal RANS-LES method to determine the flow over a high-lift configuration. Comput. Fluids 39 (7), 1241–1253.Google Scholar