Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Broglia, Riccardo
Posa, Antonio
and
Bettle, Mark C.
2020.
Analysis of vortices shed by a notional submarine model in steady drift and pitch advancement.
Ocean Engineering,
Vol. 218,
Issue. ,
p.
108236.
Posa, Antonio
2020.
Influence of Tip Speed Ratio on wake features of a Vertical Axis Wind Turbine.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 197,
Issue. ,
p.
104076.
Posa, Antonio
Broglia, Riccardo
and
Balaras, Elias
2020.
Flow over a hydrofoil in the wake of a propeller.
Computers & Fluids,
Vol. 213,
Issue. ,
p.
104714.
Posa, Antonio
Broglia, Riccardo
and
Balaras, Elias
2020.
The wake structure of a propeller operating upstream of a hydrofoil.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Zhou, Di
Wang, Kan
and
Wang, Meng
2020.
Large-Eddy Simulation of an Axisymmetric Boundary Layer on a Body of Revolution.
Liu, Yi
Zhou, Zhiteng
Zhu, Lixing
and
Wang, Shizhao
2021.
Numerical investigation of flows around an axisymmetric body of revolution by using Reynolds-stress model based hybrid Reynolds-averaged Navier–Stokes/large eddy simulation.
Physics of Fluids,
Vol. 33,
Issue. 8,
Posa, Antonio
2021.
Secondary flows in the wake of a vertical axis wind turbine of solidity 0.5 working at a tip speed ratio of 2.2.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 213,
Issue. ,
p.
104621.
Qu, Yi
Wu, Qin
Zhao, Xin
Huang, Biao
Fu, Xiaoying
and
Wang, Guoyu
2021.
Numerical investigation of flow structures around the DARPA SUBOFF model.
Ocean Engineering,
Vol. 239,
Issue. ,
p.
109866.
Posa, Antonio
2021.
Analysis of momentum recovery within the near wake of a cross-flow turbine using Large Eddy Simulation.
Computers & Fluids,
Vol. 231,
Issue. ,
p.
105178.
Posa, A.
and
Broglia, R.
2021.
Flow over a hydrofoil at incidence immersed within the wake of a propeller.
Physics of Fluids,
Vol. 33,
Issue. 12,
Panda, J. P.
and
Warrior, H. V.
2021.
Numerical Studies on Drag Reduction of An Axisymmetric Body of Revolution With Antiturbulence Surface.
Journal of Offshore Mechanics and Arctic Engineering,
Vol. 143,
Issue. 6,
Posa, Antonio
and
Broglia, Riccardo
2021.
Characterization of the turbulent wake of an axial-flow hydrokinetic turbine via large-eddy simulation.
Computers & Fluids,
Vol. 216,
Issue. ,
p.
104815.
Panda, Jyoti Prakash
Mitra, Arindam
and
Warrior, Hari V
2021.
A review on the hydrodynamic characteristics of autonomous underwater vehicles.
Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment,
Vol. 235,
Issue. 1,
p.
15.
Posa, Antonio
and
Broglia, Riccardo
2021.
Momentum recovery downstream of an axial-flow hydrokinetic turbine.
Renewable Energy,
Vol. 170,
Issue. ,
p.
1275.
Morse, Nicholas
and
Mahesh, Krishnan
2021.
Large-eddy simulation and streamline coordinate analysis of flow over an axisymmetric hull.
Journal of Fluid Mechanics,
Vol. 926,
Issue. ,
Liu, Jingcheng
Chu, Xuesen
and
Zhang, Yongming
2021.
Numerical investigation of natural transitions of bow boundary layers over underwater axisymmetric bodies.
Physics of Fluids,
Vol. 33,
Issue. 7,
Posa, Antonio
Broglia, Riccardo
and
Balaras, Elias
2021.
The wake flow downstream of a propeller-rudder system.
International Journal of Heat and Fluid Flow,
Vol. 87,
Issue. ,
p.
108765.
Posa, Antonio
Broglia, Riccardo
and
Balaras, Elias
2021.
Instability of the tip vortices shed by an axial-flow turbine in uniform flow.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Cao, Liu-shuai
Chen, Song-tao
Wan, De-cheng
and
Wang, Yi-qian
2021.
Vortex tuning of a submarine by Liutex force field model.
Journal of Hydrodynamics,
Vol. 33,
Issue. 3,
p.
503.
Jiang, Yichen
Li, Yongkun
Wu, Chongjian
Qing, Wang
and
Zhang, Guiyong
2022.
Assessment of RANS and DES turbulence models for the underwater vehicle wake flow field and propeller excitation force.
Journal of Marine Science and Technology,
Vol. 27,
Issue. 1,
p.
226.
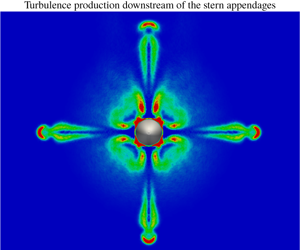
 $L$, and the free-stream velocity,
$L$, and the free-stream velocity,  $U_{\infty }$):
$U_{\infty }$):  $Re_{L}=12\times 10^{6}$ and
$Re_{L}=12\times 10^{6}$ and  $Re_{L}=1.2\times 10^{6}$. Results are in good agreement with published experiments at the same Reynolds numbers. The boundary layer thickness over the stern increases substantially at both simulated Reynolds numbers, due to the adverse pressure gradient at the rear of the body. However, for the high Reynolds number case, a weaker peak of turbulent kinetic energy develops in the outer layer over the stern. Nonetheless, the associated bimodal distribution of the turbulent stresses in the wake is already very similar a few diameters downstream of the tail. First- and second-order moments demonstrate that junction vortices at the stern bring higher velocities and turbulence at the root of the appendages for both Reynolds numbers, with a more evident signature at
$Re_{L}=1.2\times 10^{6}$. Results are in good agreement with published experiments at the same Reynolds numbers. The boundary layer thickness over the stern increases substantially at both simulated Reynolds numbers, due to the adverse pressure gradient at the rear of the body. However, for the high Reynolds number case, a weaker peak of turbulent kinetic energy develops in the outer layer over the stern. Nonetheless, the associated bimodal distribution of the turbulent stresses in the wake is already very similar a few diameters downstream of the tail. First- and second-order moments demonstrate that junction vortices at the stern bring higher velocities and turbulence at the root of the appendages for both Reynolds numbers, with a more evident signature at  $Re_{L}=12\times 10^{6}$. An azimuthal readjustment of turbulent kinetic energy occurs in the wake, becoming more axisymmetric, with increasing values in the planes aligned with the stern appendages, due to turbulence coming from both the stern boundary layer and junction vortices.
$Re_{L}=12\times 10^{6}$. An azimuthal readjustment of turbulent kinetic energy occurs in the wake, becoming more axisymmetric, with increasing values in the planes aligned with the stern appendages, due to turbulence coming from both the stern boundary layer and junction vortices.

