Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-21T15:00:24.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Number of degrees of freedom and energy spectrum of surface quasi-geostrophic turbulence

Published online by Cambridge University Press:  05 September 2011

Chuong V. Tran ,
Luke A. K. Blackbourn  and
Richard K. Scott
Chuong V. Tran*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
Luke A. K. Blackbourn
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
Richard K. Scott
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study both theoretically and numerically surface quasi-geostrophic turbulence regularized by the usual molecular viscosity, with an emphasis on a number of classical predictions. It is found that the system’s number of degrees of freedom 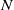, which is defined in terms of local Lyapunov exponents, scales as 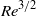, where 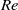is the Reynolds number expressible in terms of the viscosity, energy dissipation rate and system’s integral scale. For general power-law energy spectra 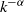, a comparison of 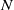with the number of dynamically active Fourier modes, i.e. the modes within the energy inertial range, yields 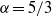. This comparison further renders the scaling 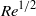for the exponential dissipation rate at the dissipation wavenumber. These results have been predicted on the basis of Kolmogorov’s theory. Our approach thus recovers these classical predictions and is an analytic alternative to the traditional phenomenological method. The implications of the present findings are discussed in conjunction with related results in the literature. Support for the analytic results is provided through a series of direct numerical simulations.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Quasi-geostrophic flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 684 , 10 October 2011 , pp. 427 - 440
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Capet, X., Hua, B. L., Lapeyre, G. & McWilliams, J. C. 2008 Surface kinetic energy transfer in surface quasi-geostrophic flows. J. Fluid Mech. 604, 165–174.Google Scholar
2. Constantin, P., E, W. & Titi, E. S. 1994 Onsager’s conjecture on the energy conservation for solutions of Euler’s equation. Commun. Math. Phys. 165, 207–209.CrossRefGoogle Scholar
3. Constantin, P., Foias, C. & Temam, R. 1988 On the dimension of attractor in two-dimensional turbulence. Physica D 30, 284–296.CrossRefGoogle Scholar
4. Constantin, P., Majda, A. & Tabak, E. 1994 Formation of strong fronts in the 2D quasi-geostrophic thermal active scalar. Nonlinearity 7, 1495–1533.Google Scholar
5. Constantin, P., Nie, Q. & Schörghofer, N. 1998 Nonsingular surface quasi-geostrophic flow. Phys. Lett. A 241, 168–172.CrossRefGoogle Scholar
6. Doering, C. R. & Gibbon, J. D. 1991 Note on the Constantin–Foias–Temam attractor dimension estimate for 2-dimensional turbulence. Physica D 48, 471–480.Google Scholar
7. Dritschel, D. G., Tran, C. V. & Scott, R. K. 2007 Revisiting Batchelor’s theory of two-dimensional turbulence. J. Fluid Mech. 591, 379–391.Google Scholar
8. Held, I. M., Pierrehumbert, R. T., Garner, S. T. & Swanson, K. L. 1995 Surface quasi-geostrophic dynamics. J. Fluid Mech. 282, 1–20.Google Scholar
9. Hou, T. Y. & Li, R. 2006 Dynamic depletion of vortex stretching and non-blowup of the 3D incompressible Euler equations. J. Nonlinear Sci. 16, 639–664.Google Scholar
10. Hou, T. Y. & Li, R. 2008 Blowup or no blowup? The interplay between theory and numerics. Physica D 237, 1937–1944.CrossRefGoogle Scholar
11. Juckes, M. N. 1994 Quasi-geostrophic dynamics of the tropopause. J. Atmos. Sci. 51, 2756–2768.2.0.CO;2>CrossRefGoogle Scholar
12. Kiselev, A., Nazarov, F. & Volberg, A. 2007 Global well-posedness for the critical 2D dissipative quasi-geostrophic equation. Invent. Math. 167, 445–453.CrossRefGoogle Scholar
13. Ohkitani, K. 2011 Growth rates analysis of scalar gradient in generalized surface quasi-geostrophic equations of ideal fluids. Phys. Rev. E 83, 036317.Google Scholar
14. Ohkitani, K. & Yamada, M. 1997 Inviscid and inviscid-limit behaviour of a surface quasigeostrophic flow. Phys. Fluids 9, 876–882.CrossRefGoogle Scholar
15. Onsager, L. 1949 Statistical hydrodynamics. Nuovo Cimento (Suppl.) 6, 279–287.Google Scholar
16. Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.CrossRefGoogle Scholar
17. Pierrehumbert, R. T., Held, I. M. & Swanson, K. L. 1994 Spectra of local and nonlocal two-dimensional turbulence. Chaos, Solitons Fractals 4, 1111–1116.Google Scholar
18. Robinson, J. C. 2003 Low dimensional attractors arise from forcing at small scales. Physica D 181, 39–44.Google Scholar
19. Scott, R. K. 2006 Local and nonlocal advection of a passive scalar. Phys. Fluids 18, 116601.CrossRefGoogle Scholar
20. Smith, K. S., Boccaletti, G., Henning, C. C., Marinov, I., Tam, C. Y., Held, I. M. & Vallis, G. K. 2002 Turbulent diffusion in the geostrophic inverse cascade. J. Fluid Mech. 469, 13–48.CrossRefGoogle Scholar
21. Temam, R. 1997 Infinite-Dimensional Dynamical Systems in Mechanics and Physics, 2nd edn. Springer.Google Scholar
22. Tran, C. V. 2009 The number of degrees of freedom of three-dimensional Navier–Stokes turbulence. Phys. Fluids 21, 125103.Google Scholar
23. Tran, C. V. & Blackbourn, L. 2009 Number of degrees of freedom of two-dimensional turbulence. Phys. Rev. E 79, 056308.Google Scholar
24. Tran, C. V. & Dritschel, D. G. 2006 Vanishing enstrophy dissipation in two-dimensional Navier–Stokes turbulence in the inviscid limit. J. Fluid Mech. 559, 107–116.CrossRefGoogle Scholar
25. Tran, C. V. & Dritschel, G. D. 2010 Energy dissipation and resolution of steep gradients in one-dimensional Burgers flows. Phys. Fluids 22, 037102.CrossRefGoogle Scholar
26. Tran, C. V., Dritschel, D. G. & Scott, R. K. 2010 Effective degrees of nonlinearity in a family of generalized models of two-dimensional turbulence. Phys. Rev. E 81, 016301.CrossRefGoogle Scholar