Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-10T14:50:13.579Z Has data issue: false hasContentIssue false
  • English
  • Français

Nucleation and growth dynamics of vapour bubbles

Published online by Cambridge University Press:  25 November 2019

Mirko Gallo ,
Francesco Magaletti ,
Davide Cocco  and
Carlo Massimo Casciola Open the ORCID record for Carlo Massimo Casciola [Opens in a new window]
Mirko Gallo
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, Via Eudossiana 18, 00184Roma, Italy
Francesco Magaletti
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, Via Eudossiana 18, 00184Roma, Italy School of Computing, Engineering and Mathematics, University of Brighton, Lewes Road, BrightonBN2 4GJ, UK
Davide Cocco
Affiliation:
Dipartimento di Scienze di Base e Applicate per l’Ingegneria, Sapienza Università di Roma, via A. Scarpa 14, 00161Roma, Italy
Carlo Massimo Casciola*
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, Via Eudossiana 18, 00184Roma, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

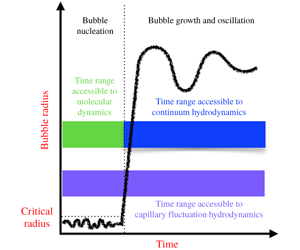
The nucleation of vapour bubbles in stretched or overheated (metastable) liquids is a complex phenomenon with a wide spectrum of applications. Several models, with different levels of detail, have been proposed to predict the key features of bubble dynamics from bubble formation up to its growth, transport and deformation. Most of them focus separately on a few of these aspects. Here, we present a thorough model based on an isothermal diffuse interface description of a two-phase liquid–vapour system endowed with thermal fluctuations, exploiting Landau and Lifshitz’s fluctuating hydrodynamic theory. The stochastic forcing allows for the spontaneous appearance of vapour clusters inside the liquid; the diffuse interface approach provides the hydrodynamic description of the subsequent growth and transport dynamics. In this work we focus on a coarse-grained version of this model, obtained through the averaging of the complete three-dimensional equations on spherical shells: the resulting stochastic equations will spatially depend on the radial distance from the vapour cluster centre. The numerical simulations give access to the mean first passage time, i.e. the time until, on average, the formation of a supercritical bubble. A rough estimate shows that the computational effort is reduced by four orders of magnitude with respect to brute-force atomistic simulations and by two orders of magnitude with respect to the full three-dimensional fluctuating model. The simulations extend up to the very long time scales, allowing us to analyse inertially driven bubble oscillations in confined systems with perfect agreement with available theoretical predictions.

JFM classification

Drops and Bubbles: Bubble dynamics Drops and Bubbles: Cavitation Multiphase and Particle-laden Flows: Multiphase flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A14
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, R. J., Valeriani, C. & ten Wolde, P. R. 2009 Forward flux sampling for rare event simulations. J. Phys.: Condens. Matter 21 (46), 463102.Google ScholarPubMed
Anderson, D. M., McFadden, G. B. & Wheeler, A. A. 1998 Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 30 (1), 139–165.CrossRefGoogle Scholar
Angélil, R., Diemand, J., Tanaka, K. K. & Tanaka, H. 2014 Bubble evolution and properties in homogeneous nucleation simulations. Phys. Rev. E 90 (6), 063301.Google ScholarPubMed
Archer, A. J. 2009 Dynamical density functional theory for molecular and colloidal fluids: a microscopic approach to fluid mechanics. J. Chem. Phys. 130 (1), 014509.Google ScholarPubMed
Balboa, F., Bell, J. B., Delgado-Buscalioni, R., Donev, A., Fai, T. G., Griffith, B. E. & Peskin, C. S. 2012 Staggered schemes for fluctuating hydrodynamics. Multiscale Model. Simul. 10 (4), 1369–1408.CrossRefGoogle Scholar
Belardinelli, D., Sbragaglia, M., Gross, M. & Andreotti, B. 2016 Thermal fluctuations of an interface near a contact line. Phys. Rev. E 94 (5), 052803.Google Scholar
Blander, M. & Katz, J. L. 1975 Bubble nucleation in liquids. AIChE J. 21 (5), 833–848.CrossRefGoogle Scholar
Brennen, C. E. 2013 Cavitation and Bubble Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Chaudhri, A., Bell, J. B., Garcia, A. L. & Donev, A. 2014 Modeling multiphase flow using fluctuating hydrodynamics. Phys. Rev. E 90 (3), 033014.Google ScholarPubMed
De Groot, S. R. & Mazur, P. 2013 Non-equilibrium Thermodynamics. Courier Dover Publications.Google Scholar
De Zarate, J. M. O. & Sengers, J. V. 2006 Hydrodynamic Fluctuations in Fluids and Fluid Mixtures. Elsevier.Google Scholar
Debenedetti, P. G. 1996 Metastable Liquids: Concepts and Principles. Princeton University Press.Google Scholar
Dell’Isola, F., Gouin, H. & Seppecher, P. 1995 Radius and surface tension of microscopic bubbles by second gradient theory. C. R. Acad. Sci. Paris II 320, 211–217.Google Scholar
Delong, S., Griffith, B. E., Vanden-Eijnden, E. & Donev, A. 2013 Temporal integrators for fluctuating hydrodynamics. Phys. Rev. E 87 (3), 033302.Google Scholar
Diemand, J., Angélil, R., Tanaka, K. K. & Tanaka, H. 2013 Large scale molecular dynamics simulations of homogeneous nucleation. J. Chem. Phys. 139 (7), 074309.Google ScholarPubMed
Diemand, J., Angélil, R., Tanaka, K. K. & Tanaka, H. 2014 Direct simulations of homogeneous bubble nucleation: agreement with classical nucleation theory and no local hot spots. Phys. Rev. E 90 (5), 052407.Google ScholarPubMed
Donev, A., Nonaka, A., Sun, Y., Fai, T., Garcia, A. & Bell, J. 2014 Low mach number fluctuating hydrodynamics of diffusively mixing fluids. Commun. Appl. Maths Comput. Sci. 9 (1), 47–105.CrossRefGoogle Scholar
Donev, A., Vanden-Eijnden, E., Garcia, A. & Bell, J. 2010 On the accuracy of finite-volume schemes for fluctuating hydrodynamics. Commun. Appl. Maths Comput. Sci. 5 (2), 149–197.CrossRefGoogle Scholar
Drysdale, C., Doinikov, A. A. & Marmottant, P. 2017 Radiation dynamics of a cavitation bubble in a liquid-filled cavity surrounded by an elastic solid. Phys. Rev. E 95 (5), 053104.Google Scholar
E, W., Ren, W. & Vanden-Eijnden, E. 2002 String method for the study of rare events. Phys. Rev. B 66 (5), 052301.CrossRefGoogle Scholar
E, W., Ren, W. & Vanden-Eijnden, E. 2007 Simplified and improved string method for computing the minimum energy paths in barrier-crossing events. J. Chem. Phys. 126 (16), 164103.Google ScholarPubMed
Español, P., Anero, J. G. & Zúñiga, I. 2009 Microscopic derivation of discrete hydrodynamics. J. Chem. Phys. 131 (24), 244117.Google ScholarPubMed
Español, P., Serrano, M. & Öttinger, H. C. 1999 Thermodynamically admissible form for discrete hydrodynamics. Phys. Rev. Lett. 83 (22), 4542.CrossRefGoogle Scholar
Flemings, M. C. 1991 Behavior of metal alloys in the semisolid state. Metall. Trans. A 22 (5), 957–981.CrossRefGoogle Scholar
Fox, R. F. & Uhlenbeck, G. E. 1970 Contributions to non-equilibrium thermodynamics. I. Theory of hydrodynamical fluctuations. Phys. Fluids 13 (8), 1893–1902.CrossRefGoogle Scholar
Gallo, M., Magaletti, F. & Casciola, C. M. 2017 Fluctuating hydrodynamics as a tool to investigate nucleation of cavitation bubbles. Intl J. Comput. Meth. Exp. Meas. 6 (2), 345–357.Google Scholar
Gallo, M., Magaletti, F. & Casciola, C. M. 2018a Phase field/fluctuating hydrodynamics approach for bubble nucleation. In ICHMT Digital Library Online. Begel House Inc.Google Scholar
Gallo, M., Magaletti, F. & Casciola, C. M. 2018b Thermally activated vapor bubble nucleation: the Landau–Lifshitz–van der Waals approach. Phys. Rev. Fluids 3, 053604.CrossRefGoogle Scholar
Gardiner, C. 2009 Stochastic Methods, vol. 4. Springer.Google Scholar
Gent, R. W., Dart, N. P. & Cansdale, J. T. 2000 Aircraft icing. Phil. Trans. R. Soc. Lond. A 358 (1776), 2873–2911.CrossRefGoogle Scholar
Goddard, B. D., Nold, A., Savva, N., Yatsyshin, P. & Kalliadasis, S. 2012 Unification of dynamic density functional theory for colloidal fluids to include inertia and hydrodynamic interactions: derivation and numerical experiments. J. Phys.: Condens. Matter. 25 (3), 035101.Google ScholarPubMed
Hohenberg, P. C. & Halperin, B. I. 1977 Theory of dynamic critical phenomena. Rev. Mod. Phys. 49 (3), 435.CrossRefGoogle Scholar
Honeycutt, R. L. 1992 Stochastic Runge–Kutta algorithms. I. White noise. Phys. Rev. A 45 (2), 600.CrossRefGoogle ScholarPubMed
Jacqmin, D. 1999 Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 155 (1), 96–127.CrossRefGoogle Scholar
Jamet, D., Lebaigue, O., Coutris, N. & Delhaye, J. M. 2001 The second gradient method for the direct numerical simulation of liquid–vapor flows with phase change. J. Comput. Phys. 169 (2), 624–651.CrossRefGoogle Scholar
Johnson, J. K., Zollweg, J. A. & Gubbins, K. E. 1993 The Lennard–Jones equation of state revisited. Mol. Phys. 78 (3), 591–618.CrossRefGoogle Scholar
Kashchiev, D. 2000 Nucleation. Elsevier.Google Scholar
Kramers, H. A. 1940 Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 7 (4), 284–304.CrossRefGoogle Scholar
LAMMPS LJ benchmarks see the LAMMPS LJ benchmarks at https://lammps.sandia.gov/bench.html#billion.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1958 Statistical Physics, Vol. 5, Course of Theoretical Physics. Pergamon.Google Scholar
Lazaridis, K., Wickham, L. & Voulgarakis, N. 2017 Fluctuating hydrodynamics for ionic liquids. Phys. Lett. A 381 (16), 1431–1438.CrossRefGoogle Scholar
Lohse, D. & Prosperetti, A. 2016 Homogeneous nucleation: patching the way from the macroscopic to the nanoscopic description. Proc. Natl Acad. Sci. USA 113 (48), 13549–13550.CrossRefGoogle ScholarPubMed
Lutsko, J. F. 2008 Density functional theory of inhomogeneous liquids. III. Liquid-vapor nucleation. J. Chem. Phys. 129 (24), 244501.Google ScholarPubMed
Lutsko, J. F. 2012 A dynamical theory of nucleation for colloids and macromolecules. J. Chem. Phys. 136 (3), 034509.Google ScholarPubMed
Lutsko, J. F. 2018 Systematically extending classical nucleation theory. New J. Phys 20, 103015.Google Scholar
Lutsko, J. F. & Durán-Olivencia, M. A. 2015 A two-parameter extension of classical nucleation theory. J. Phys.: Condens. Matter. 27 (23), 235101.Google ScholarPubMed
Magaletti, F., Gallo, M., Marino, L. & Casciola, C. M. 2016 Shock-induced collapse of a vapor nanobubble near solid boundaries. Intl J. Multiphase Flow 84, 34–45.CrossRefGoogle Scholar
Magaletti, F., Marino, L. & Casciola, C. M. 2015 Shock wave formation in the collapse of a vapor nanobubble. Phys. Rev. Lett. 114 (6), 064501.CrossRefGoogle ScholarPubMed
Marchio, S., Meloni, S., Giacomello, A., Valeriani, C. & Casciola, C. M. 2018 Pressure control in interfacial systems: atomistic simulations of vapor nucleation. J. Chem. Phys. 148 (6), 064706.Google ScholarPubMed
Meadley, S. L. & Escobedo, F. A. 2012 Thermodynamics and kinetics of bubble nucleation: simulation methodology. J. Chem. Phys. 137 (7), 074109.Google ScholarPubMed
Menzl, G., Gonzalez, M. A., Geiger, P., Caupin, F., Abascal, J. L. F., Valeriani, C. & Dellago, C. 2016 Molecular mechanism for cavitation in water under tension. Proc. Natl Acad. Sci. USA 113 (48), 13582–13587.CrossRefGoogle Scholar
Murray, B. S. 2007 Stabilization of bubbles and foams. Curr. Opin. Colloid Interface Sci. 12 (4–5), 232–241.CrossRefGoogle Scholar
Oxtoby, D. W. & Evans, R. 1988 Nonclassical nucleation theory for the gas–liquid transition. J. Chem. Phys. 89 (12), 7521–7530.CrossRefGoogle Scholar
Ren, W. 2014 Wetting transition on patterned surfaces: transition states and energy barriers. Langmuir 30 (10), 2879–2885.CrossRefGoogle ScholarPubMed
Risken, H. 1996 Fokker–Planck equation. In The Fokker–Planck Equation, pp. 63–95. Springer.CrossRefGoogle Scholar
Rowley, R. L. & Painter, M. M. 1997 Diffusion and viscosity equations of state for a Lennard–Jones fluid obtained from molecular dynamics simulations. Intl J. Thermophys. 18 (5), 1109–1121.CrossRefGoogle Scholar
Scognamiglio, C., Magaletti, F., Izmaylov, Y., Gallo, M., Casciola, C. M. & Noblin, X. 2018 The detailed acoustic signature of a micro-confined cavitation bubble. Soft Matt 14, 7987–7995.Google ScholarPubMed
Shang, B. Z., Voulgarakis, N. K. & Chu, J.-W. 2011 Fluctuating hydrodynamics for multiscale simulation of inhomogeneous fluids: mapping all-atom molecular dynamics to capillary waves. J. Chem. Phys. 135 (4), 044111.Google ScholarPubMed
Shen, V. K. & Debenedetti, P. G. 2001 Density-functional study of homogeneous bubble nucleation in the stretched Lennard–Jones fluid. J. Chem. Phys. 114 (9), 4149–4159.CrossRefGoogle Scholar
Vincent, O. & Marmottant, P. 2017 On the statics and dynamics of fully confined bubbles. J. Fluid Mech. 827, 194–224.CrossRefGoogle Scholar
Vincent, O., Marmottant, P., Gonzalez-Avila, S. R., Ando, K. & Ohl, C.-D. 2014 The fast dynamics of cavitation bubbles within water confined in elastic solids. Soft Matt. 10 (10), 1455–1461.Google ScholarPubMed
Vincent, O., Marmottant, P., Quinto-Su, P. A. & Ohl, C.-D. 2012 Birth and growth of cavitation bubbles within water under tension confined in a simple synthetic tree. Phys. Rev. Lett. 108 (18), 184502.CrossRefGoogle Scholar
Voulgarakis, N. K. & Chu, J.-W. 2009 Bridging fluctuating hydrodynamics and molecular dynamics simulations of fluids. J. Chem. Phys. 130 (13), 04B605.Google ScholarPubMed
Van der Waals, J. D. 1979 The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density. J. Stat. Phys. 20 (2), 200–244.CrossRefGoogle Scholar
Wang, Z.-J., Valeriani, C. & Frenkel, D. 2008 Homogeneous bubble nucleation driven by local hot spots: a molecular dynamics study. J. Phys. Chem. B 113 (12), 3776–3784.CrossRefGoogle Scholar