Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T03:13:55.056Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the triad interactions of homogeneous turbulence

Published online by Cambridge University Press:  21 February 2014

H. K. Moffatt
H. K. Moffatt*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

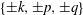Triad interactions, involving a set of wave-vectors $\{\pm \boldsymbol {k}, \pm \boldsymbol {p}, \pm \boldsymbol {q}\}$, with 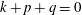$ \boldsymbol {k} + \boldsymbol {p}+ \boldsymbol {q}=0$, are considered, and the results of triad truncation are compared with the results of exact Euler evolution starting from the same initial conditions. The essential two-dimensionality of the triad interaction is used to separate the problem into two parts: a nonlinear two-dimensional flow problem in the triad plane, and a linear problem of ‘passive scalar’ type for the evolution of the component of velocity perpendicular to this plane. Several examples of triad evolution are presented in detail, and the marked contrast with Euler evolution is demonstrated. It is known that energy and helicity are conserved under triad truncation; it is shown that the ‘in-plane’ energy and enstrophy are also conserved. However, it is also shown that, in general, the evolution of the vorticity under triad truncation cannot be represented as transport by any divergence-free velocity field, with the consequence that the detailed topology of the vorticity field is not conserved under this truncation.

JFM classification

Turbulent Flows: Homogeneous turbulence Mathematical Foundations: Topological fluid dynamics Turbulent Flows: Turbulence theory
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , R3
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Biferale, L., Musacchio, S. & Toschi, F. 2013 Split energy–helicity cascades in three-dimensional homogeneous and isotropic turbulence. J. Fluid Mech. 730, 309–327.Google Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.CrossRefGoogle Scholar
Gilbert, A. D. 1988 Spiral structures and spectra in two-dimensional turbulence. J. Fluid Mech. 193, 475–497.Google Scholar
Kraichnan, R. H. 1959 The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 5, 497–543.CrossRefGoogle Scholar
Kraichnan, R. H. 1973 Helical turbulence and absolute equilibrium. J. Fluid Mech. 59, 745–752.Google Scholar
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.Google Scholar
Moffatt, H. K. 1986 On the existence of localized rotational disturbances which propagate without change of structure in an inviscid fluid. J. Fluid Mech. 173, 289–302.CrossRefGoogle Scholar
Waleffe, F. 1992 The nature of triad interactions in homogeneous turbulence. Phys. Fluids A 4, 350–363.CrossRefGoogle Scholar
Zhu, J.-Z., Yang, W. & Zhu, G.-Y. 2013 Purely helical absolute equilibria and chirality of (magneto)fluid turbulence. J. Fluid Mech. 739, 479–501.CrossRefGoogle Scholar