Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T04:42:29.702Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the stability of inviscid zonal jet flows on a rotating sphere

Published online by Cambridge University Press:  06 September 2012

Eiichi Sasaki ,
Shin-ichi Takehiro  and
Michio Yamada
Eiichi Sasaki*
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Kyoto, 606-8502, Japan
Shin-ichi Takehiro
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Kyoto, 606-8502, Japan
Michio Yamada
Affiliation:
Research Institute for Mathematical Sciences, Kyoto University, Kyoto, 606-8502, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear stability of inviscid zonal jet flows on a rotating sphere is re-examined. A semi-circle theorem for inviscid zonal flows on a rotating sphere is proved. It is also shown that numerically obtained eigenvalues of the linear stability problem do not converge well with a spectral method which was adopted in previous studies, due to an emergence of critical layers near the poles. By using a shooting method where the integral path bypasses the critical layers in the complex plane, the eigenvalues are successfully obtained with 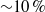correction of the critical rotation rates compared to those obtained in Baines (J. Fluid Mech., vol. 73, 1976, pp. 193–213).

JFM classification

Wakes/Jets: Jets Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 154 - 165
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Baines, P. G. 1976 The stability of planetary waves on a sphere. J. Fluid Mech. 73, 193–213.CrossRefGoogle Scholar
2. Hayashi, Y.-Y., Nishizawa, S., Takehiro, S., Yamada, M., Ishioka, K. & Yoden, S. 2007 Rossby waves and jets in two-dimensional decaying turbulence on a rotating sphere. J. Atmos. Sci. 65, 4246–4269.CrossRefGoogle Scholar
3. Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 308–321.CrossRefGoogle Scholar
4. Ishioka, K. & Yoden, S. 1992 The stability of zonal flows in barotropic fluid on a rotating sphere. Kyoto Univ. Res. Inst. Math. Sci. Kokyuroku 782, 113–124.Google Scholar
5. Kuo, H. 1949 Dynamics instability of two-dimensional nondivergent flow in a barotropic atmosphere. J. Meteorol. 6, 105–122.2.0.CO;2>CrossRefGoogle Scholar
6. Obuse, K., Takehiro, S. & Yamada, M. 2010 Long-time asymptotic states of forced two-dimensional barotropic incompressible flows on a rotating sphere. Phys. Fluids 22, 056601.CrossRefGoogle Scholar
7. Pedlosky, J. 1964 The stability of currents in the atmosphere and the ocean. Part I. J. Atmos. Sci. 21, 201–219.2.0.CO;2>CrossRefGoogle Scholar
8. Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.CrossRefGoogle Scholar
9. Skiba, Y. N. 1989 Mathematical problems of the dynamics of viscous barotropic fluid on a rotating sphere. Dept. Numer. Mathematics USSR Academy of Sciences VINITI Moscow (in Russian). 1990 Engl. Transl. Indian Institute of Tropical Meteorology. Pune, India (in English).Google Scholar
10. Skiba, Y. N. 2002 On the spectral problem in the linear stability study of flows on a sphere. J. Math. Anal. Appl. 270, 165–180.CrossRefGoogle Scholar
11. Skiba, Y. N. 2009 Linear instability of ideal flows on a sphere. Math. Meth. Appl. Sci. 32, 284–306.CrossRefGoogle Scholar
12. Thuburn, J. & Haynes, P. 1996 Bounds on the growth rate and phase velocity of instabilities in non-divergent barotropic flow on a sphere: a semicircle theorem. Q. J. R. Meteorol. Soc. 122, 779–787.Google Scholar
13. Tung, K. K. 1981 Barotropic instability of zonal flows. J. Atmos. Sci. 38, 308–321.2.0.CO;2>CrossRefGoogle Scholar