Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T15:06:52.044Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the aerodynamic splashing of droplets

Published online by Cambridge University Press:  24 May 2019

José Manuel Gordillo Open the ORCID record for José Manuel Gordillo [Opens in a new window]  and
Guillaume Riboux Open the ORCID record for Guillaume Riboux [Opens in a new window]
José Manuel Gordillo*
Affiliation:
Área de Mecánica de Fluidos, Departamento de Ingeniería Aeroespacial y Mecánica de Fluidos, Universidad de Sevilla, Avenida de los Descubrimientos s/n 41092, Sevilla, Spain
Guillaume Riboux
Affiliation:
Área de Mecánica de Fluidos, Departamento de Ingeniería Aeroespacial y Mecánica de Fluidos, Universidad de Sevilla, Avenida de los Descubrimientos s/n 41092, Sevilla, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

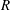When a drop of a low-viscosity liquid of radius $R$ impacts against an inclined smooth solid substrate at a velocity $V$, a liquid sheet of thickness 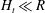$H_{t}\ll R$ is expelled at a velocity 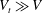$V_{t}\gg V$. If the impact velocity is such that 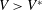$V>V^{\ast }$, with 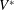$V^{\ast }$ the critical velocity for splashing, the edge of the expanding liquid sheet lifts off from the wall as a consequence of the gas lubrication force at the wedge region created between the advancing liquid front and the substrate. Here we show that the magnitude of the gas lubrication force is limited by the values of the slip length 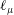$\ell _{\unicode[STIX]{x1D707}}$ at the gas–liquid interface and of the slip length 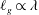$\ell _{g}\propto \unicode[STIX]{x1D706}$ at the solid, with 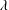$\unicode[STIX]{x1D706}$ the mean free path of gas molecules. We demonstrate that the splashing regime changes depending on the value of the ratio 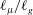$\ell _{\unicode[STIX]{x1D707}}/\ell _{g}$ – a fact explaining the spreading–splashing–spreading–splashing transition for a fixed (low) value of the gas pressure as the drop impact velocity increases (Xu et al., Phys. Rev. Lett., vol. 94, 2005, 184505; Hao et al., Phys. Rev. Lett., vol. 122, 2019, 054501). We also provide an expression for 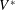$V^{\ast }$ as a function of the inclination angle of the substrate, the drop radius 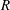$R$, the material properties of the liquid and the gas, and the mean free path 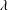$\unicode[STIX]{x1D706}$, in very good agreement with experiments.

JFM classification

Drops and Bubbles: Aerosols/atomization Drops and Bubbles: Breakup/coalescence
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , R3
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cimpeanu, R. & Moore, M. R. 2018 Early-time jet formation in liquid–liquid impact problems: theory and simulations. J. Fluid Mech. 856, 764–796.Google Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.Google Scholar
de Goede, T. C., Laan, N., de Bruin, K. G. & Bonn, D. 2018 Effect of wetting on drop splashing of Newtonian fluids and blood. Langmuir 34 (18), 5163–5168.Google Scholar
Hao, J. & Green, S. I. 2017 Splash threshold of a droplet impacting a moving substrate. Phys. Fluids 29, 012103.Google Scholar
Hao, J., Lu, J., Lee, L., Wu, Z., Hu, G. & Floryan, J. M. 2019 Droplet splashing on an inclined surface. Phys. Rev. Lett. 122, 054501.Google Scholar
Jian, Z., Josserand, C., Popinet, S., Ray, P. & Zaleski, S. 2018 Two mechanisms of droplet splashing on a solid substrate. J. Fluid Mech. 835, 1065–1086.Google Scholar
Josserand, C. & Thoroddsen, S. T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48, 365–391.Google Scholar
Josserand, C. & Zaleski, S. 2003 Droplet splashing on a thin liquid film. Phys. Fluids 15, 1650–1657.Google Scholar
Kamal, C., Sprittles, J. E., Snoeijer, J. H. & Eggers, J. 2019 Dynamic drying transition via free-surface cusps. J. Fluid Mech. 858, 760–786.Google Scholar
Lejeune, S., Gilet, T. & Bourouiba, L. 2018 Edge effect: liquid sheet and droplets formed by drop impact close to an edge. Phys. Rev. Fluids 3, 083601.Google Scholar
Marchand, A., Chan, T. S., Snoeijer, J. H. & Andreotti, B. 2012 Air entrainment by contact lines of a solid plate plunged into a viscous fluid. Phys. Rev. Lett. 108, 204501.Google Scholar
Mundo, C., Sommerfeld, M. & Tropea, C. 1995 Droplet-wall collisions: experimental studies of the deformation and breakup process. Intl J. Multiphase Flow 21, 151–173.Google Scholar
Palacios, J., Hernandez, J., Gomez, P., Zanzi, C. & Lopez, J. 2013 Experimental study of splashing patterns and the splashing/deposition threshold in drop impacts onto dry smooth solid surfaces. Exp. Therm. Fluid Sci. 44, 571–582.Google Scholar
Quintero, E. S., Riboux, G. & Gordillo, J. M. 2019 Splashing of droplets impacting superhydrophobic substrates. J. Fluid Mech. 870, 175–188.Google Scholar
Riboux, G. & Gordillo, J. M. 2014 Experiments of drops impacting a smooth solid surface: a model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113, 024507.Google Scholar
Riboux, G. & Gordillo, J. M. 2015 The diameters and velocities of the droplets ejected after splashing. J. Fluid Mech. 772, 630–648.Google Scholar
Riboux, G. & Gordillo, J. M. 2017 Boundary-layer effects in droplet splashing. Phys. Rev. E 96, 013105.Google Scholar
Scolan, Y. M. & Korobkin, A. A. 2003 Energy distribution from vertical impact of a three-dimensional solid body onto the flat free surface of an ideal fluid. J. Fluids Struct. 17, 275–286.Google Scholar
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.Google Scholar
Sprittles, J. E. 2015 Air entrainment in dynamic wetting: Knudsen effects and the influence of ambient air pressure. J. Fluid Mech. 769, 444–481.Google Scholar
Sprittles, J. E. 2017 Kinetic effects in dynamic wetting. Phys. Rev. Lett. 118, 114502.Google Scholar
Staat, H. J. J., Tran, T., Geerdink, B., Riboux, G., Sun, C., Gordillo, J. M. & Lohse, D. 2015 Phase diagram for droplet impact on superheated surfaces. J. Fluid Mech. 779, R3.Google Scholar
Stevens, C. S. 2014 Scaling of the splash threshold for low-viscosity fluids. Europhys. Lett. 106, 24001.Google Scholar
Visser, C. W., Frommhold, P. H., Wildeman, S., Mettin, R., Lohse, D. & Sun, C. 2015 Dynamics of high-speed micro-drop impact: numerical simulations and experiments at frame-to-frame times below 100 ns. Soft Matt. 11, 1708–1722.Google Scholar
Xu, L., Zhang, W. W. & Nagel, S. R. 2005 Drop splashing on a dry smooth surface. Phys. Rev. Lett. 94, 184505.Google Scholar
Supplementary material: File

Gordillo and Riboux supplementary material

Gordillo and Riboux supplementary material 1

Download Gordillo and Riboux supplementary material(File)
File 121.9 KB