Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-30T23:05:52.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Normalized dissipation rate in a moderate Taylor Reynolds number flow

Published online by Cambridge University Press:  29 March 2017

Alejandro J. Puga Open the ORCID record for Alejandro J. Puga [Opens in a new window]  and
John C. LaRue
Alejandro J. Puga*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
John C. LaRue
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Time-resolved velocity measurements are obtained using a hot-wire in a nearly homogeneous and isotropic flow downstream of an active grid for a range of Taylor Reynolds numbers from 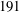$191$ to 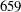$659$. It is found that the dimensionless dissipation rate, 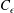$C_{\unicode[STIX]{x1D716}}$, is nearly a constant for sufficiently high values of Taylor Reynolds number, 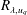$R_{\unicode[STIX]{x1D706},u_{q}}$, and is approximately equal to 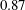$0.87$. This value is approximately 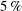$5\,\%$ less than the value reported by Bos et al. (Phys. Fluids, vol. 19 (4), 2007, 045101), which is obtained using DNS/LES (direct numerical simulation combined with large eddy simulation) for decaying homogeneous and isotropic turbulence, and is in excellent agreement with the active grid experiment of Thormann & Meneveau (Phys. Fluids, vol. 26 (2), 2014, 025112.). The results presented herein show that deviation from isotropy may cause inconsistencies in the computation of 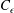$C_{\unicode[STIX]{x1D716}}$. As a result, it is suggested that the velocity scale be the square root of the turbulence kinetic energy. The integral length scale measurements obtained from the longitudinal velocity correlation are in close agreement with the integral length scale measured from the peak of the energy spectrum, 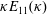$\unicode[STIX]{x1D705}E_{11}(\unicode[STIX]{x1D705})$, where $\unicode[STIX]{x1D705}$ is the wavenumber and 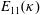$E_{11}(\unicode[STIX]{x1D705})$ is the one-dimensional power spectrum of the downstream velocity.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 184 - 204
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Pearson, B. R. 2000 Effect of initial conditions on the mean energy dissipation rate and the scaling exponent. Phys. Rev. E 62 (6), 8086.Google ScholarPubMed
Azad, R. S. 1993 Effects of hot-wire length and length-diameter ratio on spectral energy of turbulence. Meas. Sci. Technol. 4, 405–410.CrossRefGoogle Scholar
Boffetta, G. & Romano, G. P. 2002 Structure functions and energy dissipation dependence on Reynolds number. Phys. Fluids 14, 3453–3458.CrossRefGoogle Scholar
Bos, W. J., Shao, L. & Bertoglio, J. P. 2007 Spectral imbalance and the normalized dissipation rate of turbulence. Phys. Fluids 19 (4), 045101.CrossRefGoogle Scholar
Bruun, H. H. 1995 Hot-Wire Anemometry. Oxford Science.CrossRefGoogle Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2005 On the normalized turbulent energy dissipation rate. Phys. Fluids 17, 98103.CrossRefGoogle Scholar
Cao, N., Chen, S. & Doolen, G. D. 1999 Statistics and structures of pressure in isotropic turbulence. Phys. Fluids 11, 2235–2250.CrossRefGoogle Scholar
Champagne, F. H. 1978 The fine-scale structure of the turbulent velocity field. J. Fluid Mech. 86, 67–108.CrossRefGoogle Scholar
Goto, S. & Vassilicos, J. C. 2009 The dissipation rate coefficient of turbulence is not universal and depends on the internal stagnation point structure. Phys. Fluids 21, 035104.CrossRefGoogle Scholar
Hearst, R. J. & Lavoie, P. 2014 Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 741, 567–584.CrossRefGoogle Scholar
Hearst, R. J. & Lavoie, P. 2015 The effect of active grid initial conditions on high Reynolds number turbulence. Exp. Fluids 56 (10), 1–20.CrossRefGoogle Scholar
Hurst, D. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19 (3), 035103.CrossRefGoogle Scholar
Isaza, J. C., Salazar, R. & Warhaft, Z. 2014 On grid-generated turbulence in the near-and far field regions. J. Fluid Mech. 753, 402–426.CrossRefGoogle Scholar
Ishihara, T. & Kaneda, Y. 2003 High resolution DNS of incompressible homogeneous forced turbulence-time dependence of the statistics. In Statistical Theories and Computational Approaches to Turbulence, pp. 177–188. Springer.CrossRefGoogle Scholar
Kaneda, Y., Ishihara, T., Yokokawa, M., Itakura, K. I. & Uno, A. 2003 Energy dissipation rate and energy spectrum in high resolution direct numerical simulations of turbulence in a periodic box. Phys. Fluids 15, L21.CrossRefGoogle Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.CrossRefGoogle Scholar
Krogstad, P. A. & Davidson, P. A. 2011 Freely decaying, homogeneous turbulence generated by multi-scale grids. J. Fluid Mech. 680, 417–434.CrossRefGoogle Scholar
Makita, H. & Sassa, K. 1991 Active turbulence generation in a laboratory wind tunnel. Advances in Turbulence 3. pp. 497–505. Springer.CrossRefGoogle Scholar
Mazellier, N. & Vassilicos, J. C. 2008 The turbulence dissipation constant is not universal because of its universal dependence on large-scale flow topology. Phys. Fluids 20, 15101.CrossRefGoogle Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22 (7), 075101.CrossRefGoogle Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.CrossRefGoogle Scholar
Nguyen, B.2015. Calibration of an x-wire with assessment of a moderately high Reynolds number flow. Master’s thesis, University of California, Irvine, CA.Google Scholar
Nobach, H. & Tropea, C. 2012 A statistical method for transforming temporal correlation functions from one-point measurements into longitudinal spatial and spatio-temporal correlation functions. Exp. Fluids 53, 1815–1821.CrossRefGoogle Scholar
Pearson, B. R., Krogstad, P. A. & Water, W. Van De 2002 Measurements of the turbulent energy dissipation rate. Phys. Fluids 14, 1288–1290.CrossRefGoogle Scholar
Seoud, R. E. & Vassilicos, J. C. 2007 Dissipation and decay of fractal-generated turbulence. Phys. Fluids 19, 105108.CrossRefGoogle Scholar
Sreenivasan, K. R. 1984 On the scaling of the turbulence energy dissipation rate. Phys. Fluids 27, 1048–1051.CrossRefGoogle Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10, 528–529.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Thormann, A. & Meneveau, C. 2014 Decay of homogeneous, nearly isotropic turbulence behind active fractal grids. Phys. Fluids 26 (2), 025112.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2011 The decay of turbulence generated by a class of multiscale grids. J. Fluid Mech. 687, 300–340.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2014 The non-equilibrium region of grid-generated decaying turbulence. J. Fluid Mech. 744, 5–37.CrossRefGoogle Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.CrossRefGoogle Scholar
Wang, L. P., Chen, S., Brasseur, J. G. & Wyngaard, J. C. 1996 Examination of hypotheses in the kolmogorov refined turbulence theory through high-resolution simulations. Part 1. Velocity field. J. Fluid Mech. 309, 113–156.CrossRefGoogle Scholar
Webb, E. K.1955. Autocorrelations and energy spectra of atmospheric turbulencel. In Div. of Meteorological Physics Technical Paper. Australia: Commonwealth Scientific and Industrial Research Organization.Google Scholar
Wyngaard, J. C. 1968 Measurement of small-scale turbulence structure with hot wires. J. Phys. E 1, 1105.CrossRefGoogle Scholar
Yeung, P. K. & Zhou, Y. 1997 Universality of the kolmogorov constant in numerical simulations of turbulence. Phys. Rev. E 56, 1746.CrossRefGoogle Scholar